雙指針

1.三數之和

三數之和
排序 + 雙指針的方法，固定一個數nums[i], 用兩數和找target -= nums[i] 的數需要注意兩點:

1.需要去掉重復數字

while (l < r && nums[l] == nums[--l]);
while (l < r && nums[r] == nums[++r]);
....
while (i < n - 1 && nums[i] == nums[i + 1]) i++;

2.如果用這種方法去掉重復數字，那么一定要先執行 l++ && r–再去執行去重，防止有不重復數字死循環的情況發生

l++, r--;
while (l < r && nums[l] == nums[l - 1]) l++;
while (l < r && nums[r] == nums[r + 1]) r--;

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();vector<vector<int>> ans;for (int i = 0; i < n; i++) {int l = i + 1, r = n - 1;int tmptar = -nums[i];while (l < r) {if (nums[l] + nums[r] < tmptar) {l++;} else if (nums[l] + nums[r] > tmptar) {r--;} else {ans.push_back({nums[i], nums[l], nums[r]});l++, r--;while (l < r && nums[l] == nums[l - 1]) l++;while (l < r && nums[r] == nums[r + 1]) r--;}}while (i < n - 1 && nums[i] == nums[i + 1]) i++;}return ans;}
};

2.接雨水

接雨水

1. 圖1位置的水位由2，3位置決定
   
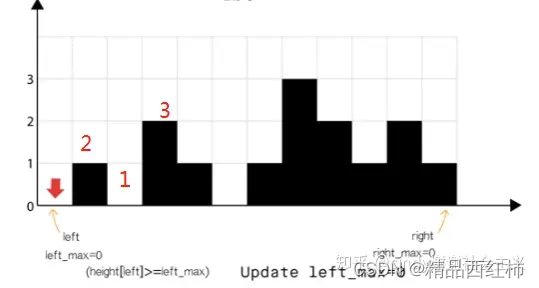
2. 雙指針相向尋找，需要找到當前遍歷過的、左右兩側的最大高度l_max, r_max
3. 如果 l_max 小于 r_max，那么左側一定能夠積水，如果 l_max 大于 r_max，右側一定能夠積水
4. 左側，只有當前的高度height[l] < l_max時才能夠有積水，否則例如 [0,1,2,3,4,5]是沒辦法形成積水的
5. 同理，右側，只有當前的高度height[r] < r_max時才能夠有積水

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int l = 0, r = n - 1, l_max = 0, r_max = 0, ans = 0;while (l <= r) {if (l_max < r_max) {l_max = max(l_max, height[l]);if (l_max > height[l]) {ans += l_max - height[l];}l++; } else {r_max = max(r_max, height[r]);if (r_max > height[r]) {ans += r_max - height[r];}r--;}}return ans;}
};

多維動態規劃

1.最長公共子序列

1）確定狀態：對于兩個字符串的動態規劃問題，套路是通用的。
比如說對于字符串 s1 和 s2，它們的長度分別是 m、n，一般來說都要構造一個這樣的 DP table：dp[m + 1][n + 1]

2）轉移方程：對于 text1：abcde 和 text2：ace 兩個字符串，我們定義兩個指針進行遍歷 i 和 j。

遍歷 text1 長度為 m，定義指針 i，從 0～m。固定 i 指針（i == 1）位置，接下來開始遍歷 text2 長度為 n，定義指針 j，從 0~n。

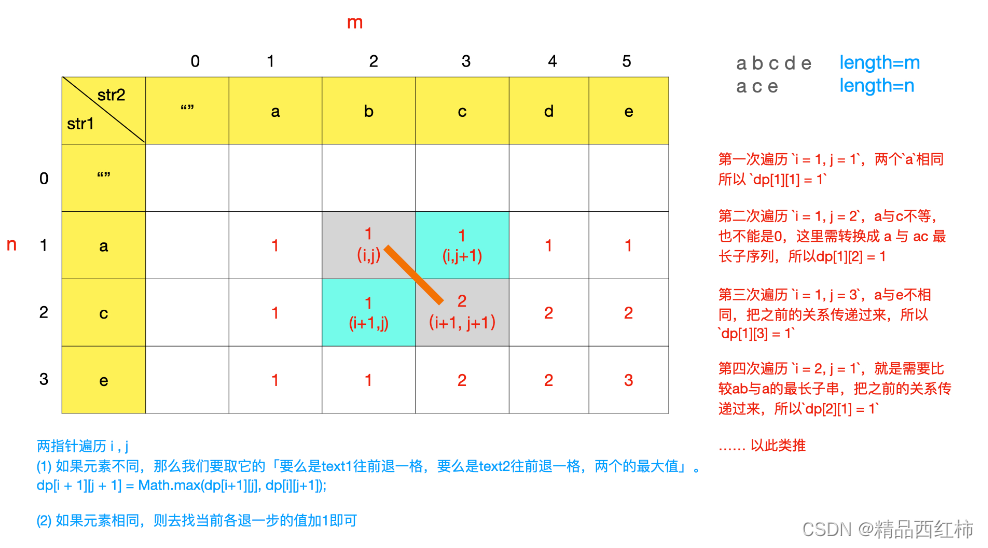
第一次遍歷 i = 1, j = 1，兩個a相同所以 dp[1][1] = 1
第二次遍歷 i = 1, j = 2，a與c不等，也不能是0，這里需轉換成 a 與 ac 最長子序列，這里需要把之前的關系傳遞過來，所以dp[1][2] = 1
第三次遍歷 i = 1, j = 3，a與e不相同，把之前的關系傳遞過來，所以dp[1][3] = 1
text2：ace 已經走完來第一輪，接下來text1：abcde 走到來b字符。

第四次遍歷 i = 2, j = 1，就是需要比較ab與a的最長子串，把之前的關系傳遞過來，所以dp[2][1] = 1

我們會發現遍歷兩個串字符，當不同時需要考慮兩層遍歷前面的值（關系傳遞），也就是左邊和上邊的其中較大的值，當相同時，需要考慮各自不包含當前字符串的子序列長度，再加上1。

因此可以得出：
現在對比的這兩個字符不相同的，那么我們要取它的「要么是text1往前退一格，要么是text2往前退一格，兩個的最大值」
dp[i + 1][j + 1] = max(dp[i+1][j], dp[i][j+1]);
對比的兩個字符相同，去找它們前面各退一格的值加1即可：dp[i+1][j+1] = dp[i][j] + 1;

3）邊界條件：dp[0][X] = 0, dp[X][0] = 0；

4）計算順序：先行后列

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n = text1.size(), m = text2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));for (int i = 1; i < n + 1; i++) {for (int j = 1; j < m + 1; j++)if (text1[i - 1] == text2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j -1]);}return dp[n][m];}
};