本專欄內容為：遞歸，搜索與回溯算法專欄。 通過本專欄的深入學習，你可以了解并掌握算法。

💓博主csdn個人主頁：小小unicorn
?專欄分類：遞歸搜索回溯專欄
🚚代碼倉庫：小小unicorn的代碼倉庫🚚
🌹🌹🌹關注我帶你學習編程知識

遞歸

什么是遞歸

在講解遞歸前，我們首先要知道什么是遞歸：
遞歸我們之前是接觸過的：
在c語言中我們詳細學過遞歸，數據結構中的快排，二叉樹也用到了遞歸。

簡單來說，遞歸就是函數自己調用自己。

為什么會用到遞歸

那么為什么會用到遞歸呢？
舉兩個例子：
例子一：
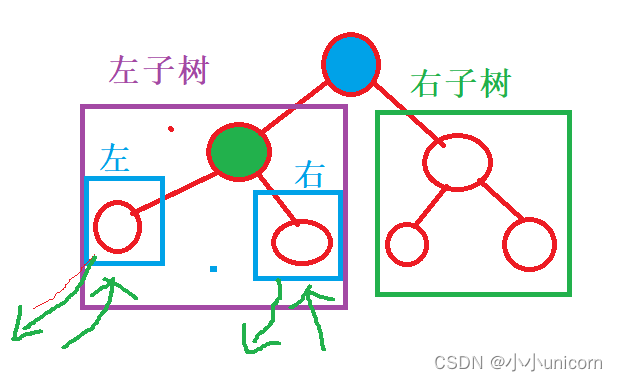
在這個二叉樹中：我們用前序遍歷來遍歷這個樹：

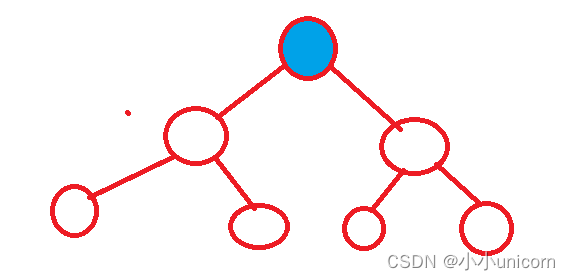
先訪問藍色節點，然后將這個樹分為左子樹和右子樹：

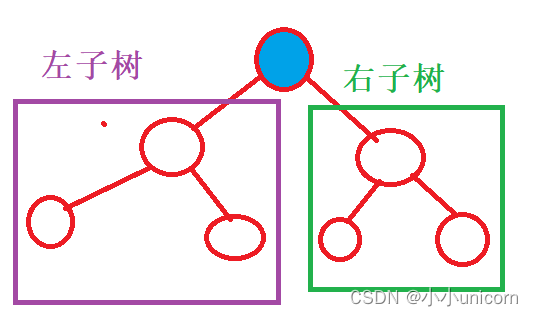
在左子樹中，我們繼續根據前序遍歷（根左右）進行劃分：

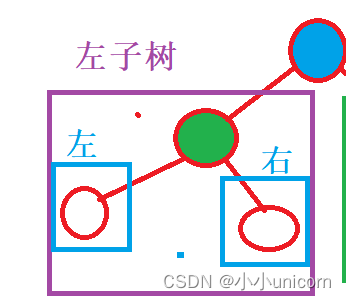
依次內推：將這個樹不停的劃分成：根，左子樹，右子樹。

我們的主問題是根左右，而子問題也是根左右，子問題的子問題的也是根左右。子問題是相同的。

例子二：
我們復習一下快排：

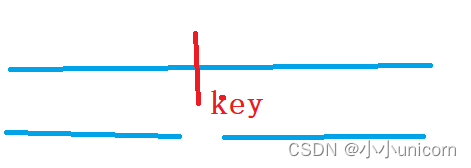
找一個key，將數組從key位置劃分為左右兩個部分，讓這兩個左右部分排序。而讓左右兩個部分排序，又可以進行劃分，在左右兩個數組繼續用Key進行劃分：

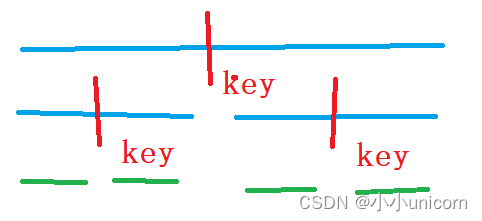
依次內推：不停的劃分，知道最后不停劃分為兩個元素后大小就很好比較。

這個例子我們也可以發現主問題是通過key將數組劃分為兩部分，而子問題也是通過key將數組劃分為兩部分，子問題的子問題也是通過key將數組劃分為兩部分。

通過這兩個例子，我們想告訴遞歸的本質：
遞歸的本質其實就是重復的子問題，也就是說主問題可以劃分成一個跟主問題相同的子問題。

如何理解遞歸

那么如何理解遞歸？
這里給出兩點：

1. 遞歸展開
2. 宏觀看待遞歸的過程

想要理解遞歸，就要畫一下遞歸的展開圖，將遞歸通過展開圖展開，會很明顯看到遞歸相關細節：返回條件，如何遞歸

其次我們要宏觀看待一個遞歸得到過程：
具體分一下幾步：

1. 不要在意遞歸的細節展開圖
2. 把遞歸的函數當成一個黑盒
3. 相信這個黑盒一定能把這件事做好

就比如我們的二叉樹后序遍歷：

首先我們要通過根節點來進行遍歷，黑盒裝什么呢？
我們知道后序是：左->右->根
那么我們就堅信dfs（root->left）一定能幫我們實現進行左子樹的遍歷，dfs（root->right）一定能幫我們實現進行右子樹的遍歷
這就相當于是我們的黑盒。

但是還要注意一個細節：
為了防止進行死循環，我們要寫一個出口（也就是返回條件）

怎樣寫好遞歸

有了上面的經驗，怎樣寫好遞歸就很簡單：

1. 先找到相同子問題（這就是我們函數頭的設計）
2. 只關心某一個問題是如何來的（這就涉及到函數體的書寫）
3. 注意細節：遞歸函數出口防止死循環
   

搜索

深度優先/寬度優先

首先要知道什么是深度優先，什么是寬度優先：
深度優先：深度優先就是一條道走到黑，我們也叫DFS，通常用遞歸實現。

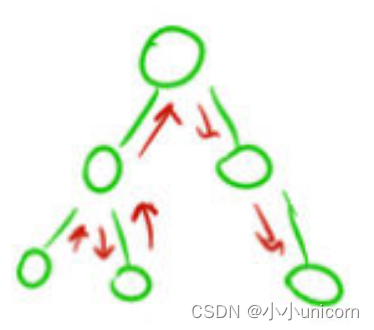
跟二叉樹遍歷一樣，從根開始，一直往下走，知道左子樹最后一個節點走完不能再走了就往上走。

寬度優先：寬度就是一層一層的剝開，我們也叫BFS，通常借助隊列實現。

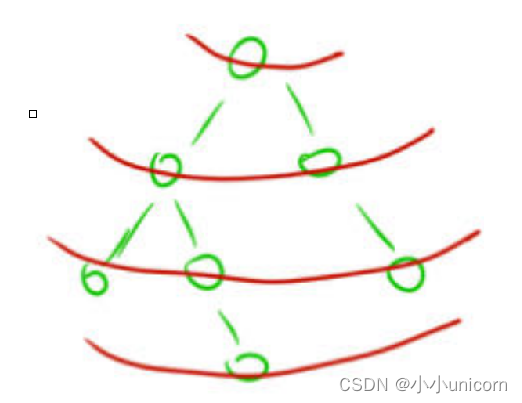
就比如還是二叉樹遍歷，我們一層一層的進行遍歷，將每一層遍歷出來。

那么深度優先遍歷和深度優先搜索又有什么區別呢？
其實遍歷和搜索大致是一樣的，記住一點：遍歷知識形式，就比如二叉樹遍歷只是根據規則進行遍歷，而搜索是遍歷里面的值，因此也叫搜索。

關系圖

其實搜索也叫暴搜，暴搜顧名思義就是暴力枚舉一遍所有的情況。

拓展搜索

其實我們之前學過的全排列就是一個搜索問題。

以123三個數的全排列為例，我們高中就學過，要想枚舉出全部的結果，用樹狀能很清晰的表達出來：

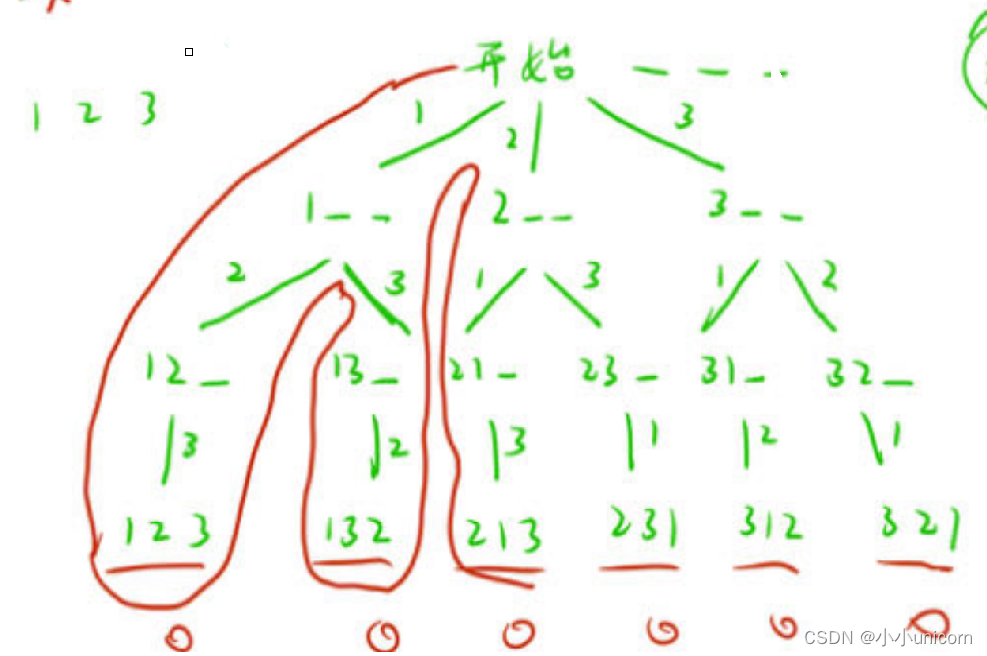
通過樹狀這樣畫出來就不會漏解的情況。

這棵樹我們也把它叫做決策樹。

回溯與剪枝

什么是回溯，什么是剪枝，其實他們兩的本質也還是搜索！！！
回溯還是以二叉樹遍歷為例：

當遍歷到左子樹的最左節點，他的左子樹為空，那么就要返回，而這個返回的過程就是回溯。

以這個迷宮為例子：

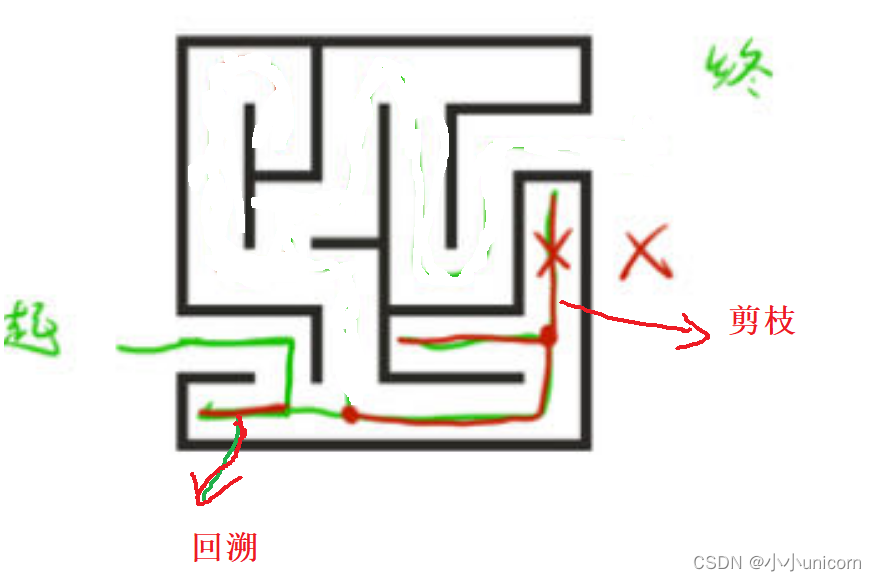
第一段紅線走到盡頭發現走不掉了，往回走的過程就是回溯。

根據暴搜原理，會一直往右走，走到盡頭，向上走，走到盡頭發現到頭了，就往回走，然后往左走，往右走，依次內推。在這個過程中，有一段是沒有必要走的路段（沒有價值的路段），在本圖中是畫叉的路段，這個畫叉的路段我們就可以舍去，舍去的過程就是剪枝。