---

前言

算法的時間復雜度和空間復雜度是評估算法性能的兩個重要指標。時間復雜度主要關注算法執行過程中所需的時間隨輸入規模的變化情況，而空間復雜度則關注算法執行過程中所需的最大存儲空間或內存空間。

對于時間復雜度，它通常表示為一個大O表示法，如O(n)、O(n^2)、O(log n)等，其中n代表輸入規模的大小。一個優秀的算法應該具有較低的時間復雜度，這意味著當輸入規模增大時，算法的執行時間增長不會過快。例如，線性時間復雜度O(n)的算法在處理大規模數據時比二次時間復雜度O(n^2)的算法更加高效。

空間復雜度同樣重要，它決定了算法執行過程中需要占用的內存空間。在某些情況下，空間復雜度甚至比時間復雜度更加關鍵，特別是在資源受限的環境中，如嵌入式系統或移動設備。因此，設計算法時需要在時間和空間之間做出權衡，以達到最佳的整體性能。

為了優化算法的時間復雜度和空間復雜度，開發者通常會采用一系列策略，如使用更高效的數據結構、減少不必要的計算、利用緩存機制等。此外，對于某些特定問題，還可以采用特定的算法設計技巧，如分治法、動態規劃、貪心算法等，來降低算法的時間復雜度和空間復雜度。

需要注意的是，算法的時間復雜度和空間復雜度并不是絕對的評估標準。在實際應用中，還需要考慮算法的其他因素，如可讀性、可維護性、可擴展性等。因此，在設計和選擇算法時，需要綜合考慮多個因素，以找到最適合特定應用場景的算法。

綜上所述，算法的時間復雜度和空間復雜度是評估算法性能的關鍵指標。通過優化這兩個指標，我們可以提高算法的執行效率，減少資源消耗，從而在實際應用中取得更好的效果。

---

一、算法效率

算法效率是評價一個算法性能優劣的重要指標，它決定了算法在處理大規模數據或復雜問題時所需的時間和空間資源。在信息技術迅猛發展的今天，算法效率的提升對于解決實際問題、提高軟件性能、優化用戶體驗等方面都具有深遠的意義。

一個高效的算法往往能夠在較短的時間內完成計算任務，減少用戶等待的時間，提升系統的響應速度。在數據處理領域，比如大數據分析、機器學習等，算法效率的高低直接關系到數據處理的速度和質量。一個高效的算法能夠在短時間內處理大量數據，提取出有價值的信息，為決策提供有力支持。

除了時間效率，算法的空間效率同樣重要。在資源有限的硬件環境下，算法的空間復雜度決定了程序能夠處理的數據規模和復雜度。一個空間效率高的算法能夠在有限的內存空間中處理更多數據，避免因為內存不足而導致的程序崩潰或性能下降。

在實際應用中，算法效率的提升往往需要通過算法優化和創新來實現。算法優化包括改進現有算法的實現方式、減少不必要的計算、利用并行計算等技術提高計算效率等。算法創新則是在原有算法的基礎上進行突破，開發出全新的算法來解決傳統算法無法高效處理的問題。

算法效率的提升對于整個信息技術領域都有著深遠的影響。它不僅能夠提高軟件系統的性能和穩定性，還能夠推動相關領域的技術進步和創新。隨著算法研究的不斷深入和發展，相信未來會有更多高效、實用的算法問世，為我們的生活和工作帶來更多的便利和可能性。

1.1 如何衡量一個算法的好壞

如何衡量一個算法的好壞呢？比如對于以下斐波那契數列：

long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

斐波那契數列的遞歸實現方式非常簡潔，但簡潔一定好嗎？那該如何衡量其好與壞呢？

1.2 算法的復雜度

算法在編寫成可執行程序后，運行時需要耗費時間資源和空間(內存)資源 。因此衡量一個算法的好壞，一般是從時間和空間兩個維度來衡量的，即時間復雜度和空間復雜度。

時間復雜度主要衡量一個算法的運行快慢，而空間復雜度主要衡量一個算法運行所需要的額外空間。在計算機發展的早期，計算機的存儲容量很小。所以對空間復雜度很是在乎。但是經過計算機行業的迅速發展，計算機的存儲容量已經達到了很高的程度。所以我們如今已經不需要再特別關注一個算法的空間復雜度。

二、時間復雜度

2.1 時間復雜度的概念

時間復雜度的定義：在計算機科學中，算法的時間復雜度是一個函數，它定量描述了該算法的運行時間。一個算法執行所耗費的時間，從理論上說，是不能算出來的，只有你把你的程序放在機器上跑起來，才能知道。但是我們需要每個算法都上機測試嗎？是可以都上機測試，但是這很麻煩，所以才有了時間復雜度這個分析方式。一個算法所花費的時間與其中語句的執行次數成正比例，算法中的基本操作的執行次數，為算法的時間復雜度。

即：找到某條基本語句與問題規模N之間的數學表達式，就是算出了該算法的時間復雜度。

// 請計算一下Func1中++count語句總共執行了多少次？
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

Func1 執行的基本操作次數 ：

• N = 10 F(N) = 130
• N = 100 F(N) = 10210
• N = 1000 F(N) = 1002010

實際中我們計算時間復雜度時，我們其實并不一定要計算精確的執行次數，而只需要大概執行次數，那么這里我們使用大O的漸進表示法。

2.2 大O的漸進表示法

大O符號（Big O notation）：是用于描述函數漸進行為的數學符號。

推導大O階方法：

1. 用常數1取代運行時間中的所有加法常數。
2. 在修改后的運行次數函數中，只保留最高階項。
3. 如果最高階項存在且不是1，則去除與這個項目相乘的常數。得到的結果就是大O階。

使用大O的漸進表示法以后，Func1的時間復雜度為：

• N = 10 F(N) = 100
• N = 100 F(N) = 10000
• N = 1000 F(N) = 1000000

通過上面我們會發現大O的漸進表示法去掉了那些對結果影響不大的項，簡潔明了的表示出了執行次數。

另外有些算法的時間復雜度存在最好、平均和最壞情況：

• 最壞情況：任意輸入規模的最大運行次數(上界)
• 平均情況：任意輸入規模的期望運行次數
• 最好情況：任意輸入規模的最小運行次數(下界)

例如：在一個長度為N數組中搜索一個數據x

• 最好情況：1次找到
• 最壞情況：N次找到
• 平均情況：N/2次找到

在實際中一般情況關注的是算法的最壞運行情況，所以數組中搜索數據時間復雜度為O(N)

2.3常見時間復雜度計算舉例

實例1：

// 計算Func2的時間復雜度？
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

實例2:

// 計算Func3的時間復雜度？
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}

實例3:

// 計算Func4的時間復雜度？
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}

實例4:

// 計算strchr的時間復雜度？
const char * strchr ( const char * str, int character );

實例5:

// 計算BubbleSort的時間復雜度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

實例6:

// 計算BinarySearch的時間復雜度？
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]：begin和end是左閉右閉區間，因此有=號while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}

實例7:

// 計算階乘遞歸Fac的時間復雜度？
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}

實例8:

// 計算斐波那契遞歸Fib的時間復雜度？
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

實例答案及分析：

1. 實例1基本操作執行了2N+10次，通過推導大O階方法知道，時間復雜度為 O(N)
2. 實例2基本操作執行了M+N次，有兩個未知數M和N，時間復雜度為 O(N+M)
3. 實例3基本操作執行了10次，通過推導大O階方法，時間復雜度為O(1)
4. 實例4基本操作執行最好1次，最壞N次，時間復雜度一般看最壞，時間復雜度為 O(N)
5. 實例5基本操作執行最好N次，最壞執行了(N*(N+1)/2次，通過推導大O階方法+時間復雜度一般看最壞，時間復雜度為 O(N^2)
6. 實例6基本操作執行最好1次，最壞O(logN)次，時間復雜度為 O(logN)
   ps：logN在算法分析中表示是底數為2，對數為N。有些地方會寫成lgN。
7. 實例7通過計算分析發現基本操作遞歸了N次，時間復雜度為O(N)。
8. 實例8通過計算分析發現基本操作遞歸了2^N次，時間復雜度為O(2^N)。

2.4等差數列計算公式

等差數列的計算公式是：

第n項: an = a1 + (n-1)d

其中，an表示第n項，a1表示首項，d表示公差。

等差數列求和公式如下：

Sn = (n/2)(2a + (n - 1)d)

Sn = (n/2)(a1 + an)

其中Sn表示等差數列的前n項和，a表示首項，d表示公差，n表示項數。

a1代表第一項，an代表第n項

例子：

求等差數列1, 3, 5, 7, 9的前5項和。

首項a = 1，公差d = 2，項數n = 5。

代入公式得到：

S5 = (5/2)(2*1 + (5 - 1)*2)= (5/2)(2 + 8)= (5/2)(10)= 25

所以1, 3, 5, 7, 9的前5項和為25。

2.5等比數列計算方法

等比數列是指數列中，任意兩個相鄰的數的比值都是一個常數。計算等比數列的方法有兩種：根據公式計算和逐項計算。

1. 根據公式計算：
   等比數列的通項公式為：an = a1 * q^(n-1)，其中a1是首項，q是公比，n是項數。
   根據此公式，可以直接計算出數列中的任意一項。

2. 逐項計算：
   根據等比數列的定義，可以逐項計算數列中的每一項。首先確定首項a1和公比q，然后按照以下步驟進行計算：

• 第1項為a1。
• 第2項為a1 * q。
• 第3項為第2項 * q。
• 以此類推，每一項都是前一項乘以公比q。

等比數列的求和公式為：Sn = a1 * (1 - q^n) / (1 - q)，其中a1是首項，q是公比，n是項數。

根據這個公式，可以直接計算等比數列的和。

舉例說明：
假設有一個等比數列：2, 4, 8, 16, 32，要求求和。

首項a1=2，公比q=2，項數n=5。

根據求和公式，代入對應的值進行計算：

Sn = 2 * (1 - 2^5) / (1 - 2)= 2 * (1 - 32) / (-1)= 2 * (-31) / (-1)= 62

所以，這個等比數列的和為62。

三、空間復雜度

空間復雜度也是一個數學表達式，是對一個算法在運行過程中臨時占用存儲空間大小的量度 。

空間復雜度不是程序占用了多少bytes的空間，因為這個也沒太大意義，所以空間復雜度算的是變量的個數。

空間復雜度計算規則基本跟實踐復雜度類似，也使用大O漸進表示法。

注意：函數運行時所需要的棧空間(存儲參數、局部變量、一些寄存器信息等)在編譯期間已經確定好了，因此空間復雜度主要通過函數在運行時候顯式申請的額外空間來確定。

實例1：

// 計算BubbleSort的空間復雜度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

實例2：

// 計算Fibonacci的空間復雜度？
// 返回斐波那契數列的前n項
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}

實例3：

// 計算階乘遞歸Fac的空間復雜度？
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}

實例答案及分析：

1. 實例1使用了常數個額外空間，所以空間復雜度為 O(1)

2. 實例2動態開辟了N個空間，空間復雜度為 O(N)

3. 實例3遞歸調用了N次，開辟了N個棧幀，每個棧幀使用了常數個空間。空間復雜度為O(N)

四、 常見復雜度對比

一般算法常見的復雜度如下：

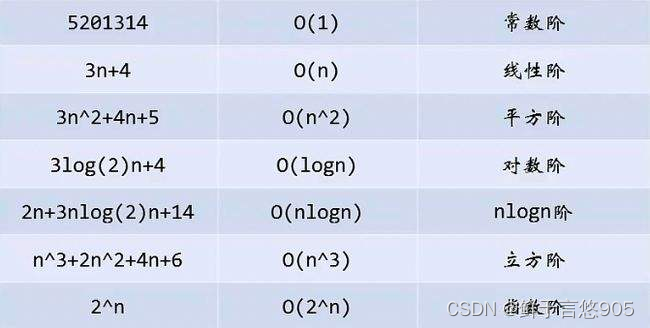
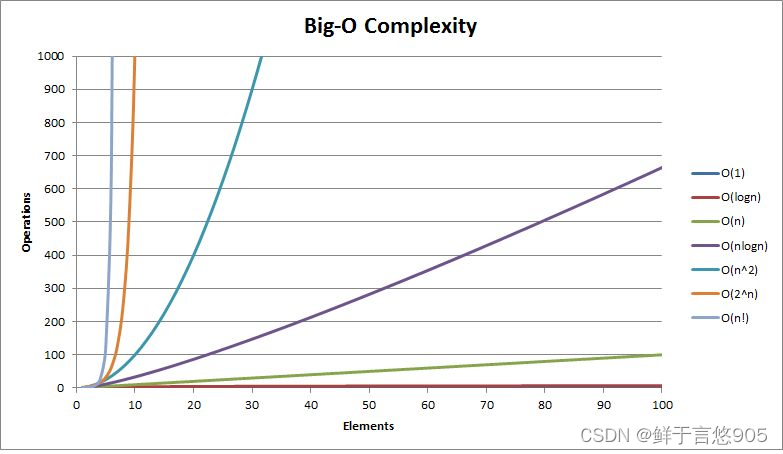
五、 復雜度的oj練習

3.1消失的數字OJ鏈接

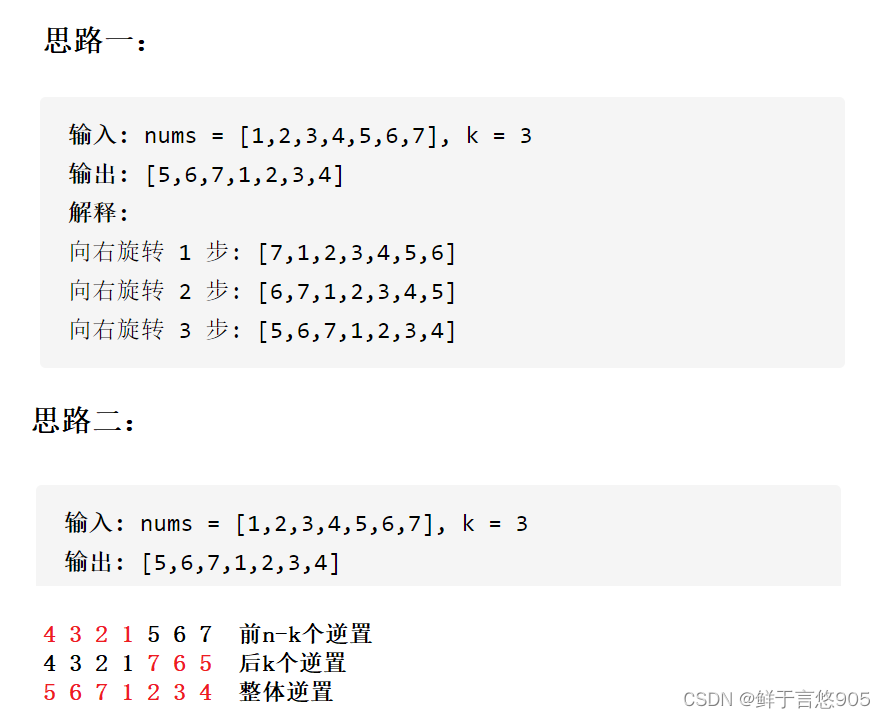
3.2 旋轉數組OJ鏈接

---