目錄
1?主要內容
目標函數
重要約束條件
2?部分代碼
3?程序結果
4 下載鏈接
1?主要內容
該程序復現《高比例清潔能源接入下計及需求響應的配電網重構》,以考慮網損成本、棄風棄光成本和開關操作懲罰成本的綜合成本最小為目標,針對配電網重構模型的非凸性,引入中間變量并對其進行二階錐松弛,構建混合整數凸規劃模型,采用改進的 IEEE33 節點配電網進行算例仿真,分析了需求響應措施和清潔能源滲透率對配電網重構結果的影響。該程序復現效果和出圖較好(詳見程序結果部分),注釋清楚,方便學習!
注意:該程序運行環境為matlab+mosek,需要各位同學下載并安裝mosek求解器,通過官網可以申請學術許可,可免費使用365天。

-
目標函數
目標函數為配電網綜合運行成本最小,其中考慮了網損成本、棄風棄光成本以及分段開關操作懲罰成本。

-
重要約束條件
常規的功率平衡、節點電壓電流等約束不再贅述,重點分析一下網絡結構約束和需求響應約束。
網絡結構約束:
配電網在重構過程中需滿足連通性約束與輻射狀約束,具體模型為:

該網絡結構約束是采用虛擬潮流方式,之前有幾個重構代碼也是采用虛擬潮流形式,參考的是《A New Model for Resilient Distribution Systems?by Microgrids Formation》,具體模型如下:

仔細觀察不難發現,上面的模型是下面的簡潔版,在不考慮分布式電源節點對網絡切割情況下,兩者是等價的。
經驗證(見結果圖最后一張),該種約束方式下能夠保證網絡的連通性和輻射性。
需求響應約束:
在配電網中采用需求響應策略,可以在降低負荷峰谷差的同時,減少配電網運行的綜合成本,提高配電網運行的經濟性和可靠性。

在該模型中,電價彈性系數為已知量,需求響應前后總負荷保持一致。
2?部分代碼
%% 系統參數 mpc = IEEE33; % 風光負荷曲線 P_wind0=[0.21 0.07 0.11 0.21 0.38 0.42 0.12 0.19 0.22 0.47 0.55 0.71 0.80 0.99 0.89 0.99 0.99 0.98 0.99 0.99 0.98 0.77 0.61 0.19]; P_pv0=[0 0 0 0 0.17 0.24 0.40 0.54 0.60 0.51 0.35 0.29 0.27 0.25 0.18 0.10 0.06 0 0 0 0 0 0 0]; P_L0=[0.37 0.33 0.31 0.28 0.27 0.28 0.28 0.27 0.26 0.24 0.30 0.76 0.82 0.86 0.76 0.54 0.43 0.65 0.81 0.95 0.99 0.91 0.65 0.19]; nb=33; % 節點數 ns=1; % 電源節點數 nl=37; % 支路數 n_pv=2; % 光伏數 n_wind=3; % 風機數 n_ess=2; % 儲能數 T=24; % 調度時段總數 F=0.6; % 滲透率 P_DG=sum(mpc.bus(:,3))*F/mpc.baseMVA/5; % DG額定容量 P_wind_max=P_DG*P_wind0; % 風機最大有功 P_pv_max=P_DG*P_pv0; % 光伏最大有功 P_load=mpc.bus(:,3)/mpc.baseMVA*P_L0; % 有功負荷 Q_load=mpc.bus(:,4)/mpc.baseMVA*P_L0; % 無功負荷 Sij_max=15/mpc.baseMVA; % 支路功率最大值 r_ij=mpc.branch(:,3)*ones(1,T); % 線路電阻 x_ij=mpc.branch(:,4)*ones(1,T); % 線路電抗 wind=[9 25 32]; % 風機接入位置 pv=[17 22]; % 光伏接入位置 ess=[7 25]; % 儲能接入位置 Umax=[1;1.06*1.06*ones(32,1)]; % 電壓上限的平方 Umin=[1;0.94*0.94*ones(32,1)]; % 電壓下限的平方 I_max=10; % 電流上限值 P_ch_max=0.2/mpc.baseMVA; % 充電功率上限0.2MW P_dis_max=0.2/mpc.baseMVA; % 放電功率上限0.2MW E_min=0.15/mpc.baseMVA; % 儲能容量下限0.15MWh E_max=0.8/mpc.baseMVA; % 儲能容量上限0.8MWh n_ch=0.9; % 充電效率為0.9 n_dis=0.85; % 放電效率為0.85 E0=0.3/mpc.baseMVA; % 初始荷電狀態為0.3MWh Q_CB_st=0.15/mpc.baseMVA; % 單個電容器無功補償容量0.15Mvar N_CB_max=5; % 最大可投切電容器數目 ksai=0.5; % 彈性系數 c1=3; % 網絡損耗成本系數3元/kWh c2=1.2; % 棄風棄光懲罰系數1.2元/kWh c3=15; % 分段開關操作懲罰成本系數15元/次 rho=zeros(1,24); % 分時電價 rho([12:15,19:23])=1.026; % 峰時電價 rho([7:11,16:18])=0.691; % 平時電價 rho([1:6,24])=0.2561; % 谷時電價 rho0=0.35; % 初始節點電價為0.35元/kWh M=1.1*1.1 - 0.9*0.9; % 中間變量 P_g_max=10/mpc.baseMVA; % 電源有功功率最大值 Q_g_max=10/mpc.baseMVA; % 電源無功功率最大值 branch_to_node=zeros(nb,nl); % 流入節點的支路 branch_from_node=zeros(nb,nl); % 流出節點的支路 for k=1:nlbranch_to_node(mpc.branch(k,2),k)=1; %舉例說明,k=1,流入節點2是支路1;同時流出節點1的是支路1;同理,k=2,流入節點3且流出節點2的是支路2;這一步建立支路和節點的連接關系branch_from_node(mpc.branch(k,1),k)=1; end ? %% 優化變量 alpha_ij=binvar(nl,1); % 支路開斷情況 U_i=sdpvar(nb,T); % 電壓的平方 I_ij=sdpvar(nl,T); % 電流的平方 P_ij=sdpvar(nl,T); % 線路有功功率 Q_ij=sdpvar(nl,T); % 線路無功功率 P_wind=sdpvar(n_wind,T); % 風機輸出功率 P_pv=sdpvar(n_pv,T); % 光伏輸出功率 Q_wind=sdpvar(n_wind,T); % 風機輸出功率 Q_pv=sdpvar(n_pv,T); % 光伏輸出功率 P_ch=sdpvar(n_ess,T); % 儲能充電功率 P_dis=sdpvar(n_ess,T); % 儲能充電功率 y_ch=binvar(n_ess,T); % 儲能充電狀態 y_dis=binvar(n_ess,T); % 儲能放電狀態 E_ESS=sdpvar(n_ess,T); % 儲能荷電狀態 N_CB=intvar(1); % 投切的電容器數量 P_cur=sdpvar(nb,T); % 需求響應后的負荷量 P_g=sdpvar(nb,T); % 節點注入有功 Q_g=sdpvar(nb,T); % 節點注入無功 P_g_dot=sdpvar(nb,1); % 虛擬電源 P_L_dot=ones(nb,1); % 虛擬負荷 P_ij_dot=sdpvar(nl,1); % 虛擬功率 ? %% 約束條件 Constraints = []; %% 1.潮流約束 m_ij=(1-alpha_ij)*M*ones(1,T); Constraints = [Constraints, P_g-P_cur+branch_to_node*P_ij-branch_to_node*(I_ij.*r_ij)-branch_from_node*P_ij == 0]; Constraints = [Constraints, Q_g-Q_load+branch_to_node*Q_ij-branch_to_node*(I_ij.*x_ij)-branch_from_node*Q_ij == 0]; Constraints = [Constraints,U_i(mpc.branch(:,1),:)-U_i(mpc.branch(:,2),:)<= m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij]; Constraints = [Constraints,U_i(mpc.branch(:,1),:)-U_i(mpc.branch(:,2),:)>= -m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij]; for k=1:nlfor t=1:TConstraints = [Constraints, cone([2*P_ij(k,t) 2*Q_ij(k,t) I_ij(k,t)-U_i(mpc.branch(k,1),t)],I_ij(k,t)+U_i(mpc.branch(k,1),t))];end end Constraints = [Constraints, Sij_max^2*alpha_ij*ones(1,T) >= P_ij.^2+Q_ij.^2]; Constraints = [Constraints, I_max.^2.*alpha_ij*ones(1,T) >= I_ij , I_ij >= 0]; Constraints = [Constraints, Umin*ones(1,T) <= U_i,U_i <= Umax*ones(1,T)]; ? %% 2.拓撲約束 Constraints = [Constraints , sum(alpha_ij) == nb-ns]; Constraints = [Constraints , P_g_dot(2:33) == 0 , P_g_dot(1) <= nb]; Constraints = [Constraints , P_g_dot-P_L_dot+branch_to_node*P_ij_dot-branch_from_node*P_ij_dot == 0]; ? %% 3.DG功率約束 Constraints = [Constraints , P_pv >= 0 , P_wind >= 0]; Constraints = [Constraints , P_pv <= ones(n_pv,1)*P_pv_max , P_wind <= ones(n_wind,1)*P_wind_max]; ? %% 4.儲能約束 Constraints = [Constraints , P_ch >= 0 , P_dis >= 0 , y_ch+y_dis <= 1]; Constraints = [Constraints , P_ch <= y_ch*P_ch_max , P_dis <= y_dis*P_dis_max]; Constraints = [Constraints , E_ESS(:,1) ==n_ch*P_ch(:,1)-1/n_dis*P_dis(:,1)+E0]; Constraints = [Constraints , E_ESS >= E_min , E_ESS <= E_max]; for t=2:TConstraints = [Constraints , E_ESS(:,t) ==n_ch*P_ch(:,t)-1/n_dis*P_dis(:,t)+E_ESS(:,t-1)]; end ?
3?程序結果

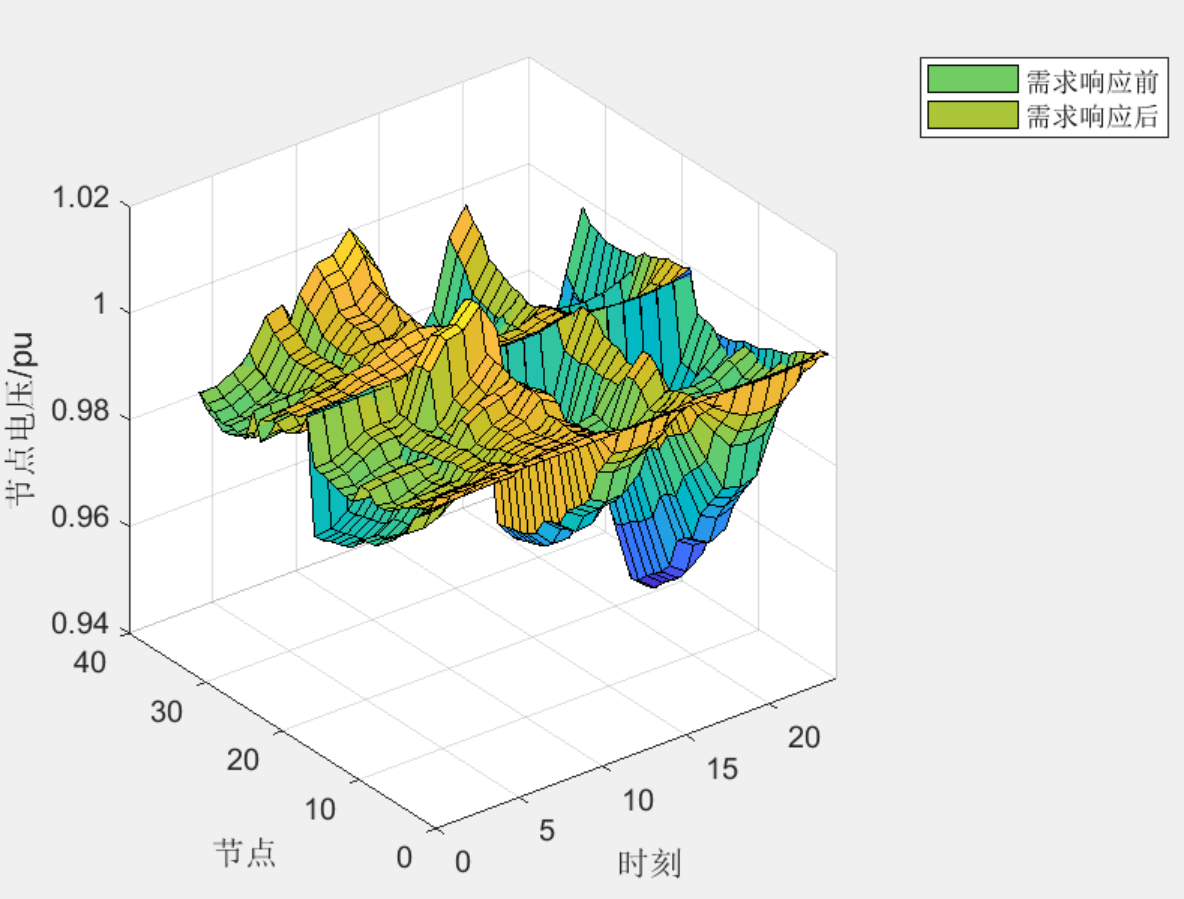
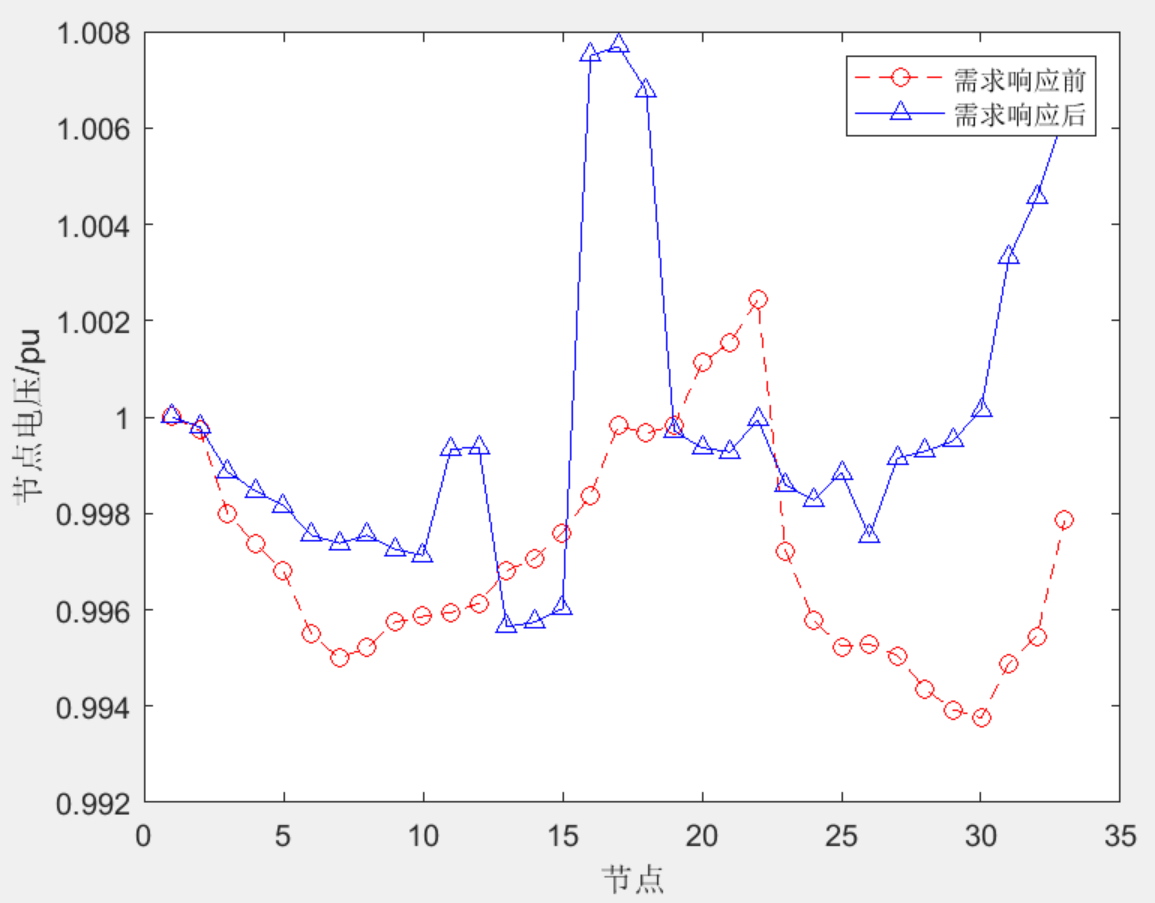



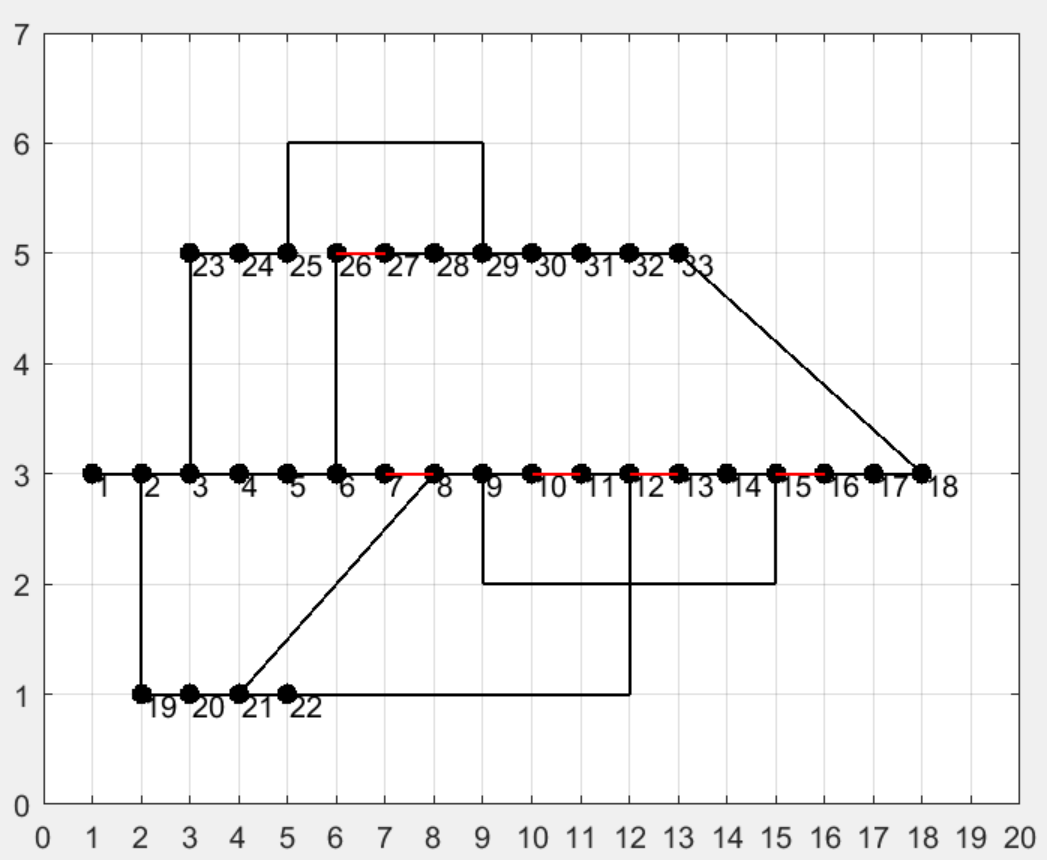


)
- 06覆蓋索引)







)






)
