數據結構題目①—

前言

本篇文章為博主進行代碼隨想錄——數組練習后的總結會涉及到每一道題目的詳細的思路整理，以及本人的易錯點，希望對大家有所幫助

數組介紹：

數組在C語言中就已經有所涉及，它是一個最基礎的數據結構，而在數據結構中，通常它屬于線性表中的順序表（Sequence List）,它是一種特殊的線性存儲結構。

特點：

邏輯上相鄰的數據元素，在物理次序上也是相鄰的。——也就是說它們挨著存儲

任意元素都可在相同的時間內存取，即順序存儲的數組是一個隨即存取結構

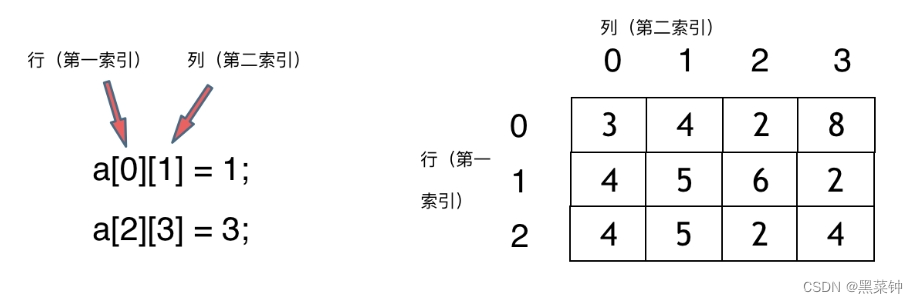
順序存儲：行優先和列優先兩種順序

行優先——每一行的第一個元素位于低地址，最后的位于高地址，且連續

列優先——每一行的第一個元素位于低地址，最后的位于高地址，且連續

優點：

它訪問速度快，但是無法高效插入和刪除元素

數組理論基礎

數組是存放在連續內存空間上的相同類型數據的集合

數組的元素是不能刪的，只能覆蓋

如果使用C++的話，要注意vector 和 array的區別，vector的底層實現是array，嚴格來講vector是容器，不是數組。

對于二維數組來說——它的順序是否連續呢——語言不同，會造成一定的差異，而c++中的二維數組是連續的，Java卻不是這樣存儲的。

?二分查找

題目：. - 力扣（LeetCode）

方法——使用二分查找的方式

注意——

1.要看清題目是否給出有序數組，這是一個二分查找的條件

2.循環不變量的思想——區間設置到底是左閉右開還是左閉右閉

第一次寫可能出現的問題——

1.if中的==而不是=

2.left和right是數組的位置標號，而非數組內容

3.要注意從開始就考慮是選取左閉右閉還是左閉右開

4.注意函數最后要在while循環外有一個return 否則錯誤

二分查找的方法介紹：

?二分法就是設置兩個指針，讓它們一個在最左邊，一個在最右邊，而且要設置一個中間值然后為了查找有序數組中的值，不斷細分這個數組——假如你要尋找的這個數是小于中間值的，那么這個數就在左邊，這時候我們只需要在左邊再次重復操作——直到左邊指針和右邊指針找到了那個數（這個結束的條件有兩種情況）

那這樣寫第一遍你會發現——可能還是會發生錯誤——

在while循環中，結束的條件到底是left<right還是left<=right呢？

在循環中找到要繼續查找的是左邊或右邊后，right或left是等于middle（中間值）呢，還是其他呢？

那么接下來就介紹一個概念——循環不變量?

在整個過程中我們這個數組在查找時，是把它看成左閉右閉還是左閉右開呢？這個需要你在循環之前需要搞清楚的量，就是所謂的循環不變量

當左閉右閉時——

1.while括號里的條件為——left<=right因為這時left=right對于閉區間來說，是成立的
2.而當需要移動指針時，right或者是left是直接等于middle-1/middle+1的，因為已經判斷好了middle上不是需要找的數.

當左閉右開時——

1.while括號里的條件為——left<right因為這時left=right對于半開區間來說，是不成立的
2.而當需要移動指針時，right是直接等于middle的，因為這時候right是一個開區間，只有放在已查看過的middle，才不至于略掉其他的可能為你要尋找的數

學會之后：第二次可能寫出現的問題——

對于左閉右開的形式，從一開始就需要做出改變

——

1.定義時，右邊的要定義的比左閉右閉多一位

2.對于左邊的變到中間，是中間+1，因為這里是閉區間

3.對于右邊的變到中間，就是中間了

更多有關二分查找的題（也來自代碼隨想錄）
35.搜索插入位置(opens new window)
34.在排序數組中查找元素的第一個和最后一個位置(opens new window)
69.x 的平方根(opens new window)
367.有效的完全平方數(opens new window)

這里只記錄一個二分查找擴展——搜索插入位置

暴力解法

class Solution {
public:int searchInsert(vector<int>& nums, int target) {for (int i = 0; i < nums.size(); i++) {// 分別處理如下三種情況// 目標值在數組所有元素之前// 目標值等于數組中某一個元素// 目標值插入數組中的位置if (nums[i] >= target) { // 一旦發現大于或者等于target的num[i]，那么i就是我們要的結果return i;}}// 目標值在數組所有元素之后的情況return nums.size(); // 如果target是最大的，或者 nums為空，則返回nums的長度}
};

二分法（這里采用c++其中的vector<int>& nums相當于C語言中傳入一個整型數組nums，nums.size()返回這個數組的大小）

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int n = nums.size();int left = 0;int right = n; // 定義target在左閉右開的區間里，[left, right)  targetwhile (left < right) { // 因為left == right的時候，在[left, right)是無效的空間int middle = left + ((right - left) >> 1);if (nums[middle] > target) {right = middle; // target 在左區間，在[left, middle)中} else if (nums[middle] < target) {left = middle + 1; // target 在右區間，在 [middle+1, right)中} else { // nums[middle] == targetreturn middle; // 數組中找到目標值的情況，直接返回下標}}// 分別處理如下四種情況// 目標值在數組所有元素之前 [0,0)// 目標值等于數組中某一個元素 return middle// 目標值插入數組中的位置 [left, right) ，return right 即可// 目標值在數組所有元素之后的情況 [left, right)，因為是右開區間，所以 return rightreturn right;}
};

移除元素

題目：. - 力扣（LeetCode）

第一遍練習會出現的問題——

對于i不知道如何讓它再次看之前的數值——i--即可

第二次循環時，需要覆蓋，這時候要設置j=i+1,n[j]=n[j-1]

?方法一——暴力解題法

對于移除元素，在循環中找到所滿足條件的數組元素，然后覆蓋其位置數值（用循環）……

方法二——快慢指針法

首先來介紹一下什么是快指針和慢指針：

具體方法思路——

首先假設數組為[3,2,2,3]需要去除的值是3

快慢指針初始均指向第一個數，慢指針是為了獲取最終數組，它這個位置假如遇到需要去除的值，則要覆蓋——快指針獲取這個覆蓋的值，即最后把所有的需要去除的數給去除。

所以循環是現判斷快指針指向的位置是否為需要去除的值——是則往下移一位，不是則把這個值賦給慢指針所指向的值，然后慢指針往后移，循環往復，直到快指針遍歷結束

例子：假如第一個遇到的就是需要去除的值，那么快指針會先往下一步，然后如果所指向的值不為去除的值——賦值給慢指針，這樣可以覆蓋掉第一個需要去除的值，然后慢指針往后一步，如果慢指針還是指向需要去除的值，則重復上述步驟，這樣直到最后，快指針可以把所有的不需要去除的值給按順序覆蓋到需要去除的地方——完成代碼即可

int removeElement(int* nums, int numsSize, int val) {int s=0;int q=0;for(;q<numsSize;q++){if(nums[q]!=val){nums[s]=nums[q];s++;}}return s;
}

注意寫代碼時——這里的快慢指針不是真的指針，而是設置的數組下標。

有序數組的平方

題目：. - 力扣（LeetCode）

第一次暴力解題會出現的問題——

1.平方的for循環要i從0——numsSize(<號的時候)

2.排序方式——這里用選擇排序示例：

for(int i=0;i<numsSize-1;i++){for(int j=i+1;j<numsSize;j++){if(nums[i]>nums[j]){int t=nums[i];nums[i]=nums[j];nums[j]=t;}}}

第二次用雙指針寫出現的問題——

1.新建的數組需要動態開辟空間？

雙指針法

設計思路：

首先先觀察題目——發現如果平方之后，最大值一定是最左邊或是最右邊的平方，而且是按一定順序排列的數組，如果是右邊的平方大，則下一個就是左邊的平方，然后再往里比較，因此這里借助兩個指針，一左一右，進行大小比較，然后把大的一個賦值給新數組

?雙指針法的具體思路：

首先先創造一個新數組——和原來的數組一樣大小，這里使用動態數組的方式，然后設置兩個int類型的數據，它們分別為0和數組大小-1，然后比較這兩個所指的原數組數據平方誰大——誰就把這個放進新數組的最右邊，然后這個指針往中間的方向移動——再次比較——再次賦值給新數組的“指針”……直到兩個指針相遇，即可結束循環——代碼也就完成了

代碼：（result是新數組）

class Solution {
public:vector<int> sortedSquares(vector<int>& A) {int k = A.size() - 1;vector<int> result(A.size(), 0);for (int i = 0, j = A.size() - 1; i <= j;) { if (A[i] * A[i] < A[j] * A[j])  {result[k--] = A[j] * A[j];j--;}else {result[k--] = A[i] * A[i];i++;}}return result;}
};

長度最小的子數組

題目：

. - 力扣（LeetCode）

第一次寫出現的問題——

1.沒有思路

2.返回值？

3.這個int類型的最大值不知道是怎么寫？

INT32_MAX

?這里的思路其實看過代碼之后就有點恍然大悟了，但是不知道怎么想的，很妙

這道題依然采用兩個指針的方法——不過這里方法叫滑動窗口，因為可能指針的移動像滑動吧🤭

1.由于返回的是長度最小的滿足情況的數組大小——因此我們先把這個長度設置為最大——也就是int的最大，用INT32_MAX來表示，如果最后結果仍未這個值，說明沒有滿足條件的情況，返回0，否則返回長度的最小值。

2.這里使用雙指針的原因是——整個數組的滿足范圍不限制，而其中的每一組組合都可能滿足，如果想要簡便的實現的話，需要兩個指針，它們不斷變換，我們求其中的總值，如果滿足情況，則賦值給返回值，最后不斷更新返回值的較小值，就可找到返回值最小的情況，題目也就滿足了

滑動窗口的代碼實現：

這里兩個分別是指針1和指針2（剛開始都在同一位置），需要之間的值大于7，先設置一個sum的初始值為0,進入循環中，加上n[j]，如果這時候的sum>=7，則直接給result賦值1，如果不是——指針j往下移動，然后循環內又再加上n[j]……直到指針指向第二個2時，sum>=7了，則先賦值給result一個較小值，然后指針1開始移動——尋找這個滿足條件的區間內可以有更小的可能嗎？（這時候需要減去n[i]后移動這個指針），然后發現從3——2區間也成立，然后再循環，直到指針循環到最后，result自然=最小值

代碼：

class Solution {
public:int minSubArrayLen(int s, vector<int>& nums) {int result = INT32_MAX;int sum = 0; // 滑動窗口數值之和int i = 0; // 滑動窗口起始位置int subLength = 0; // 滑動窗口的長度for (int j = 0; j < nums.size(); j++) {sum += nums[j];// 注意這里使用while，每次更新 起始位置，并不斷比較子序列是否符合條件while (sum >= s) {subLength = (j - i + 1); // 取子序列的長度result = result < subLength ? result : subLength;sum -= nums[i++]; // 這里體現出滑動窗口的精髓之處，不斷變更i（子序列的起始位置）}}// 如果result沒有被賦值的話，就返回0，說明沒有符合條件的子序列return result == INT32_MAX ? 0 : result;}

?這個時間復雜度為O（n）——這個是看每一個元素被操作的次數，因為有兩個指針，每個元素在滑動窗進來一次出去一次，時間復雜度為2n——O（n）

螺旋矩陣

題目：59. 螺旋矩陣 II - 力扣（LeetCode）

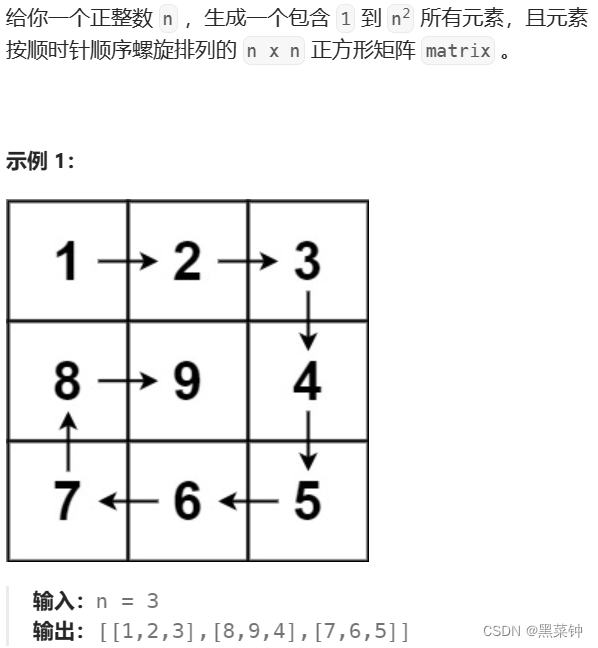
這個和二分法一樣，需要有不變量——左閉右開，

而這里發生錯誤的地方在于——

1.要知道每一個矩陣需要繞的圈數——n/2,

2.注意一圈過后，它的起始位置發生改變，要都加1

3.如果n為奇數的話，最后要判斷一下，單獨把中間的值賦值

?注意如何在c語言中動態初始化二維數組：

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){//初始化返回的結果數組的大小*returnSize = n;*returnColumnSizes = (int*)malloc(sizeof(int) * n);//初始化返回結果數組ansint** ans = (int**)malloc(sizeof(int*) * n);
}

復習——malloc和free

free參數要么是NULL要么是之前從malloc、calloc、realloc返回的值，無返回值

malloc返回一塊連續的數組，返回類型為void*，C和C++規定，void*類型可以強制轉換為任何其他類型的指針

而malloc里面放的是需要空間的大小，一般用sizeof來計算?

注意：

要檢查所請求的內存是否分配成功

必須要釋放

可以使用exit(1)——用于退出整個程序，終止進程，返回1代表異常終止，返回0正常退出

?方法——模擬行為，這里重要的就是考慮循環不變量，而除此之外其它的也很重要——其中的思想，模擬過程

這其實是一個二維數組的初始化，不過更為復雜，這里看代碼——

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定義一個二維數組int startx = 0, starty = 0; // 定義每循環一個圈的起始位置int loop = n / 2; // 每個圈循環幾次，例如n為奇數3，那么loop = 1 只是循環一圈，矩陣中間的值需要單獨處理int mid = n / 2; // 矩陣中間的位置，例如：n為3， 中間的位置就是(1，1)，n為5，中間位置為(2, 2)int count = 1; // 用來給矩陣中每一個空格賦值int offset = 1; // 需要控制每一條邊遍歷的長度，每次循環右邊界收縮一位int i,j;while (loop --) {i = startx;j = starty;// 下面開始的四個for就是模擬轉了一圈// 模擬填充上行從左到右(左閉右開)for (j = starty; j < n - offset; j++) {res[startx][j] = count++;}// 模擬填充右列從上到下(左閉右開)for (i = startx; i < n - offset; i++) {res[i][j] = count++;}// 模擬填充下行從右到左(左閉右開)for (; j > starty; j--) {res[i][j] = count++;}// 模擬填充左列從下到上(左閉右開)for (; i > startx; i--) {res[i][j] = count++;}// 第二圈開始的時候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)startx++;starty++;// offset 控制每一圈里每一條邊遍歷的長度offset += 1;}// 如果n為奇數的話，需要單獨給矩陣最中間的位置賦值if (n % 2) {res[mid][mid] = count;}return res;}
};

時間復雜度 O(n^2): 模擬遍歷二維矩陣的時間
空間復雜度 O(1）