過擬合和欠擬合

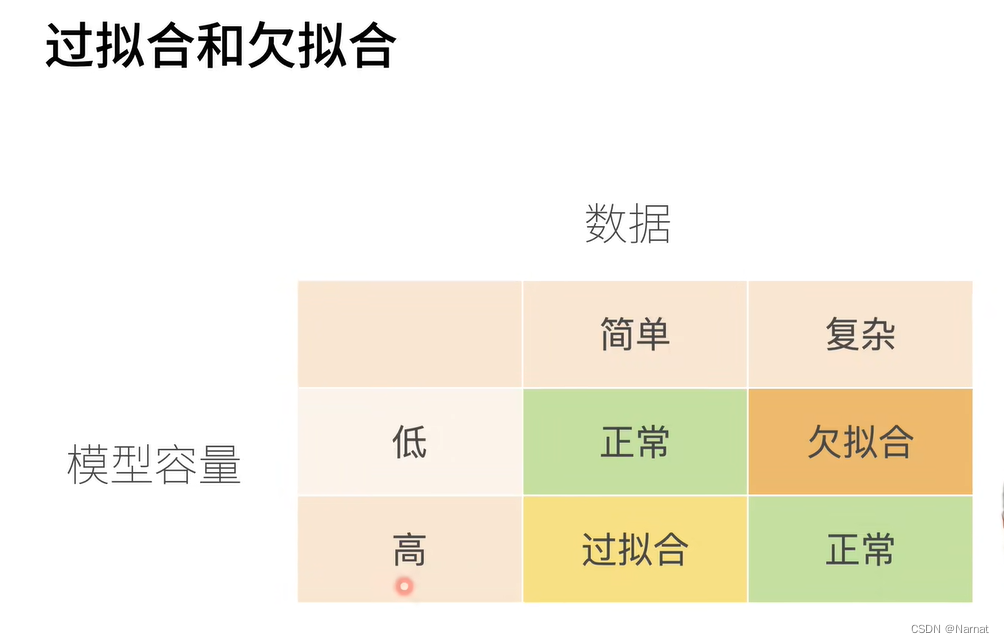
過擬合和欠擬合是訓練模型中常會發生的事，如所要識別手勢過于復雜，如五角星手勢，那就需要更改高級更復雜的模型去訓練，若用比較簡單模型去訓練，就會導致模型未能抓住手勢的全部特征，那簡單模型估計只能抓住五角星的其中一個角做特征，那么這個簡單模型很可能就會將三角形與五角星混淆，這就是所謂欠擬合

若用識別五角星的復雜模型去識別三角形也是不行的，模型會過擬合，即學習了過多不重要的部分，可能會把三角形每條邊所畫的時間也當作學習的內容，即便我們人知道什么時候畫哪條邊都無所謂。

過擬合和欠擬合的表現都是模型的識別精度不夠，所以要想判斷模型是過擬合還是欠擬合，除了理論還是要多調試

如：

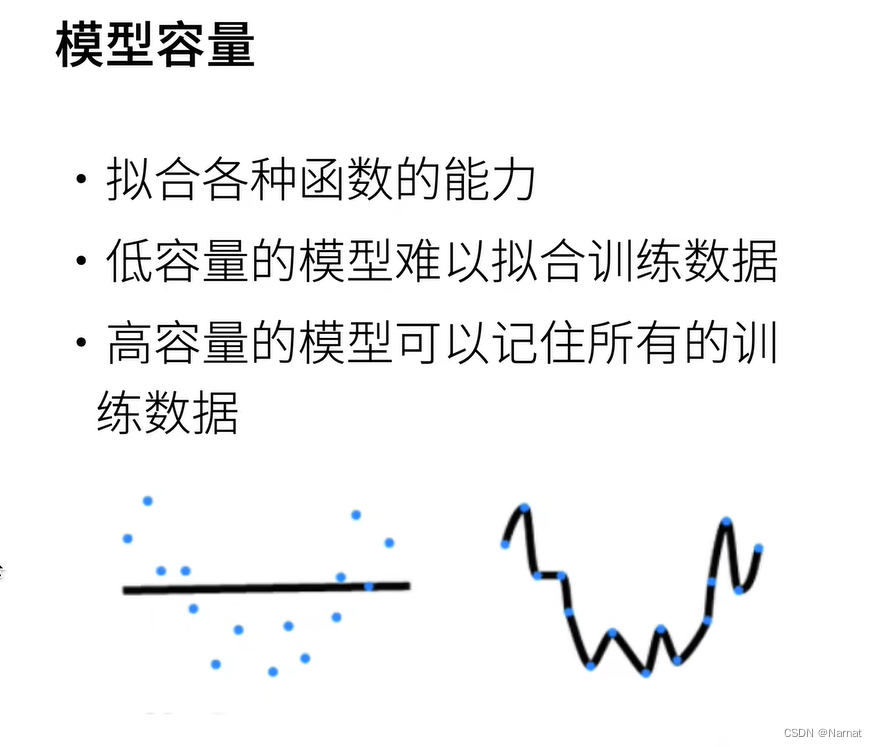
合適的模型應該是拋物線，上述左邊是欠擬合，右邊是過擬合

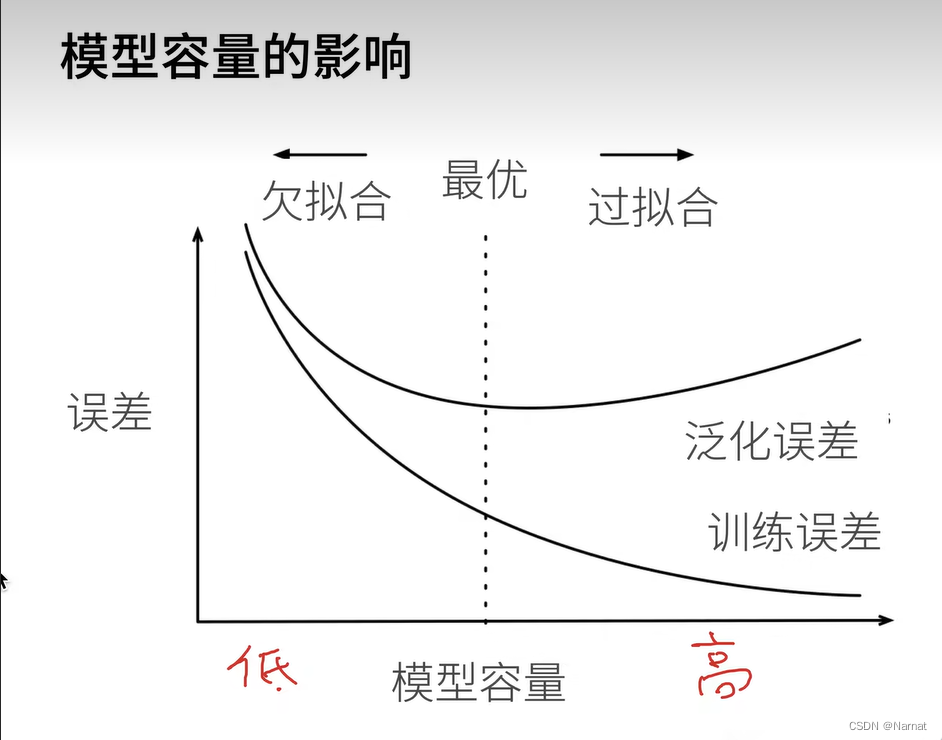
訓練集和測試集

值得注意的是訓練集和測試集必須是分開的，訓練模型用訓練集，一定不能讓測試集污染模型

模型過擬的特征即對見過的數據集表現非常好，而對從未見過的模型表現非常差，若不把訓練，測試集完全分開，最后的模型過擬合將無法被發現

實例：

完整代碼：

import math
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt# 生成隨機的數據集
max_degree = 20  # 多項式的最大階數
n_train, n_test = 100, 100  # 訓練和測試數據集大小
true_w = torch.zeros(max_degree)
true_w[0:4] = torch.Tensor([5, 1.2, -3.4, 5.6])# 生成特征
features = torch.randn((n_train + n_test, 1))
permutation_indices = torch.randperm(features.size(0))
# 使用隨機排列的索引來打亂features張量（原地修改）
features = features[permutation_indices]
poly_features = torch.pow(features, torch.arange(max_degree).reshape(1, -1))
for i in range(max_degree):poly_features[:, i] /= math.gamma(i + 1)# 生成標簽
labels = torch.matmul(poly_features, true_w)
labels += torch.normal(0, 0.1, size=labels.shape)# 以下是你原來的訓練函數，沒有修改
def evaluate_loss(net, data_iter, loss):metric = d2l.Accumulator(2)for X, y in data_iter:out = net(X)y = y.reshape(out.shape)l = loss(out, y)metric.add(l.sum(), l.numel())return metric[0] / metric[1]def train(train_features, test_features, train_labels, test_labels,num_epochs=400):loss = nn.MSELoss()input_shape = train_features.shape[-1]net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))batch_size = min(10, train_labels.shape[0])train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),batch_size)test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),batch_size, is_train=False)trainer = torch.optim.SGD(net.parameters(), lr=0.01)# 用于存儲訓練和測試損失的列表train_losses = []test_losses = []for epoch in range(num_epochs):train_loss, train_acc = d2l.train_epoch_ch3(net, train_iter, loss, trainer)test_loss = evaluate_loss(net, test_iter, loss)# 將當前的損失值添加到列表中train_losses.append(train_loss)test_losses.append(test_loss)print(f"Epoch {epoch + 1}/{num_epochs}:")print(f"  訓練損失： {train_loss:.4f}, 測試損失： {test_loss:.4f}")print(net[0].weight)# 假設 train_losses 和 test_losses 是已經計算出的損失值列表plt.figure(figsize=(10, 6))plt.plot(train_losses, label='train', color='blue', linestyle='-', marker='.')plt.plot(test_losses, label='test', color='purple', linestyle='--', marker='.')plt.xlabel('epoch')plt.ylabel('loss')plt.title('Loss over Epochs')plt.legend()plt.grid(True)plt.ylim(0, 100)  # 設置y軸的范圍從0.01到100plt.show()# 選擇多項式特征中的前4個維度
train(poly_features[:n_train, :4], poly_features[n_train:, :4],labels[:n_train], labels[n_train:])

分部講解如下：

問題實例：

產生高斯分布隨機數x并按上述式子生成訓練集和驗證集y，并對生成的y再添加一些雜音處理
注意：訓練集一定要打亂，不要排序，排序會讓訓練效果大打折扣，如果訓練數據是按照某種特定順序排列的，那么模型可能會學習到這種順序并在這個過程中引入偏差，導致模型在未見過的新數據上的泛化能力下降，打亂訓練集的目的通常是為了防止模型學習到訓練數據中的任何順序依賴性，這樣可以提高模型在隨機或未見過的新數據上的泛化能力。

# 生成隨機的數據集
max_degree = 20  # 多項式的最大階數
n_train, n_test = 100, 100  # 訓練和測試數據集大小
true_w = torch.zeros(max_degree)
true_w[0:4] = torch.Tensor([5, 1.2, -3.4, 5.6])# 生成特征
features = torch.randn((n_train + n_test, 1))
permutation_indices = torch.randperm(features.size(0))
# 使用隨機排列的索引來打亂features張量（原地修改）
features = features[permutation_indices]
poly_features = torch.pow(features, torch.arange(max_degree).reshape(1, -1))
for i in range(max_degree):poly_features[:, i] /= math.gamma(i + 1)# 生成標簽
labels = torch.matmul(poly_features, true_w)
labels += torch.normal(0, 0.1, size=labels.shape)

計算損失函數，并不會更新迭代模型，所以用他來測試模型測試集損失

def evaluate_loss(net, data_iter, loss):metric = d2l.Accumulator(2)for X, y in data_iter:out = net(X)y = y.reshape(out.shape)l = loss(out, y)metric.add(l.sum(), l.numel())return metric[0] / metric[1]

訓練函數，將X和對應y放在一起，即是進行模型迭代更新，又能計算模型訓練損失，測試損失并繪制相應圖形

def train(train_features, test_features, train_labels, test_labels,num_epochs=400):loss = nn.MSELoss()  # 默認取平均損失input_shape = train_features.shape[-1]  # 模型大小取train_features最后一項大小net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))batch_size = min(10, train_labels.shape[0])  # 整體數據集分成<= 10批次train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),batch_size)test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),batch_size, is_train=False)trainer = torch.optim.SGD(net.parameters(), lr=0.01)  # 梯度下降算法# 用于存儲訓練和測試損失的列表train_losses = []test_losses = []for epoch in range(num_epochs):train_loss, train_acc = d2l.train_epoch_ch3(net, train_iter, loss, trainer)  # 訓練迭代模型test_loss = evaluate_loss(net, test_iter, loss)# 將當前的損失值添加到列表中train_losses.append(train_loss)test_losses.append(test_loss)print(f"Epoch {epoch + 1}/{num_epochs}:")print(f"  訓練損失： {train_loss:.4f}, 測試損失： {test_loss:.4f}")print(net[0].weight)  # 輸出訓練好的模型# 假設 train_losses 和 test_losses 是已經計算出的損失值列表plt.figure(figsize=(10, 6))plt.plot(train_losses, label='train', color='blue', linestyle='-', marker='.')plt.plot(test_losses, label='test', color='purple', linestyle='--', marker='.')plt.xlabel('epoch')plt.ylabel('loss')plt.title('Loss over Epochs')plt.legend()plt.grid(True)plt.ylim(0, 100)  # 設置y軸的范圍從0.01到100plt.show()

主函數

# 選擇多項式特征中的前4個維度
train(poly_features[:n_train, :4], poly_features[n_train:, :4],labels[:n_train], labels[n_train:])

利用上述實例驗證欠擬合和過擬合以及正常擬合

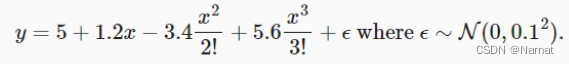
上述函數對應真正的模型為：

true_w[0:4] = torch.Tensor([5, 1.2, -3.4, 5.6])

當然還有一些雜質，可忽略

那么可知預訓練模型取四個維度就能做到正常擬合，而取二十個維度就是過擬合，取四個以下維度就是欠擬合

過擬合即取二十維度效果：

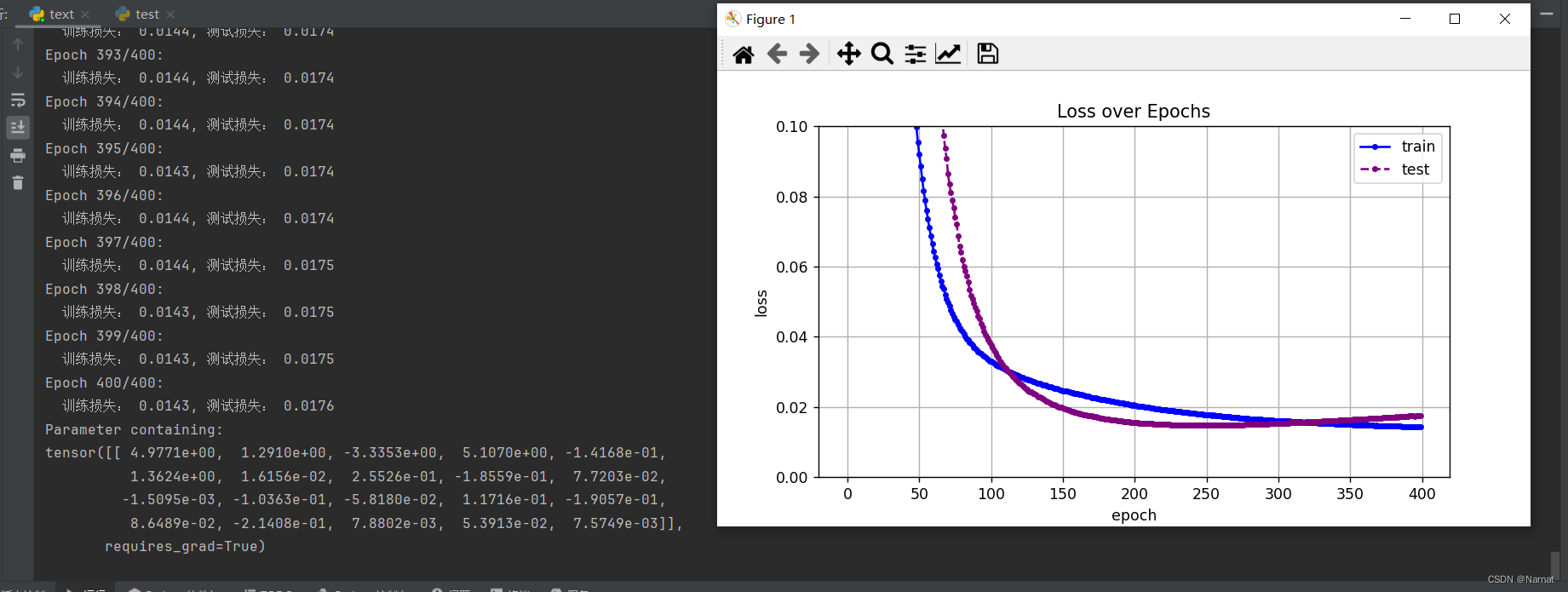
可以看出損失在下降到最低點的時候還會有上升

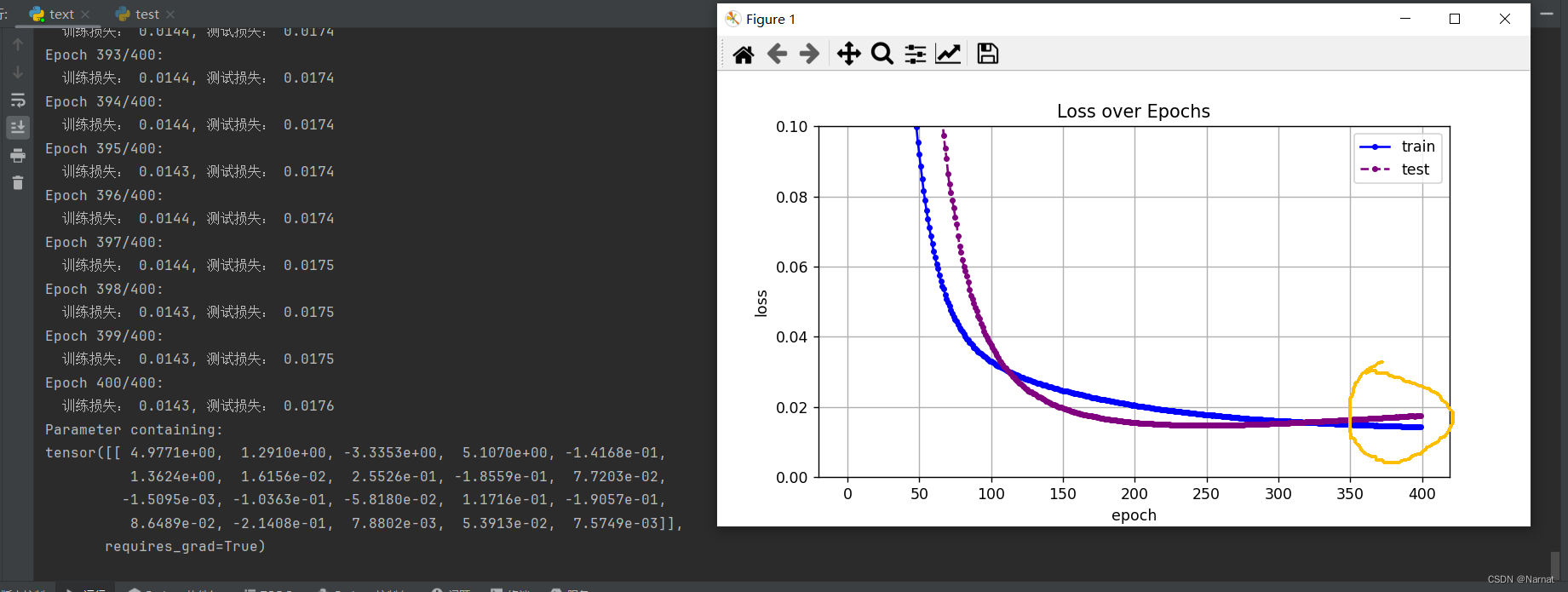
這是因為學完主要四個維度后又將本應是0的維度也學習了，也就是學習了無用的雜質。

欠擬合二維度模型效果：

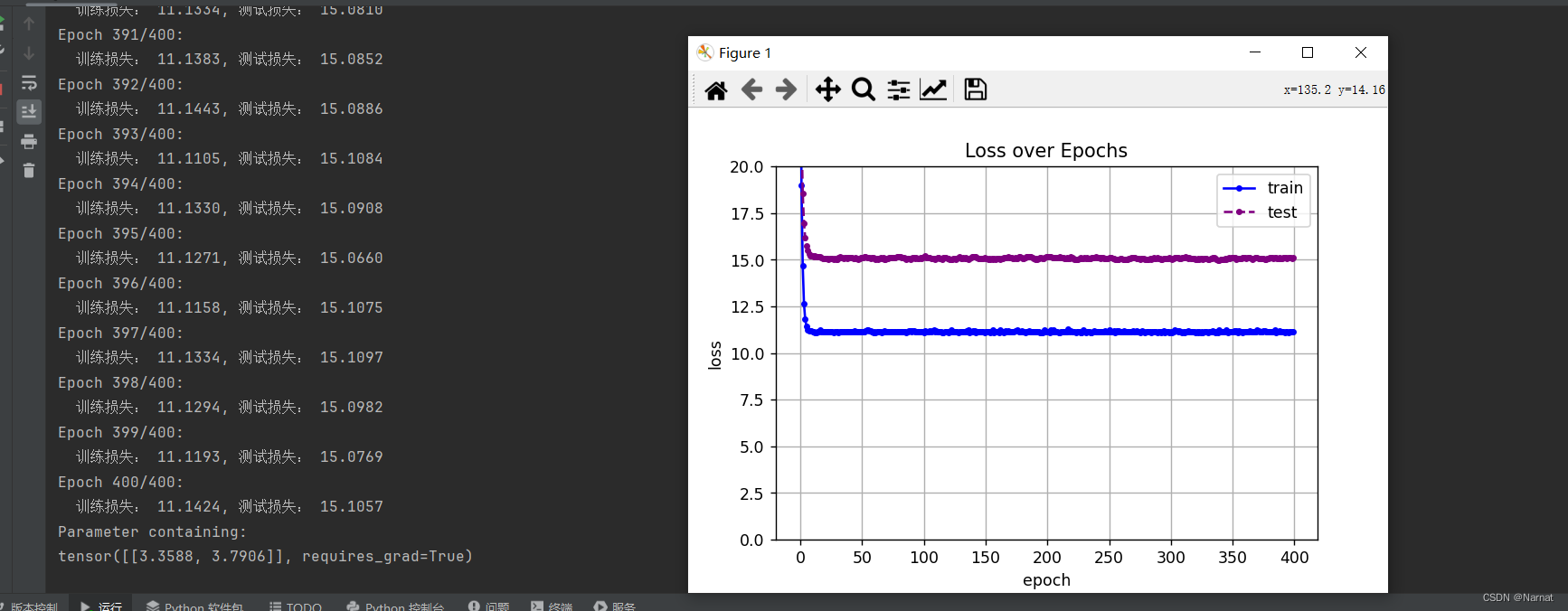
損失很大,這也是沒辦法，畢竟還有很多重要維度沒有學習上，本質上是模型過小

正常擬合四維度模型效果：

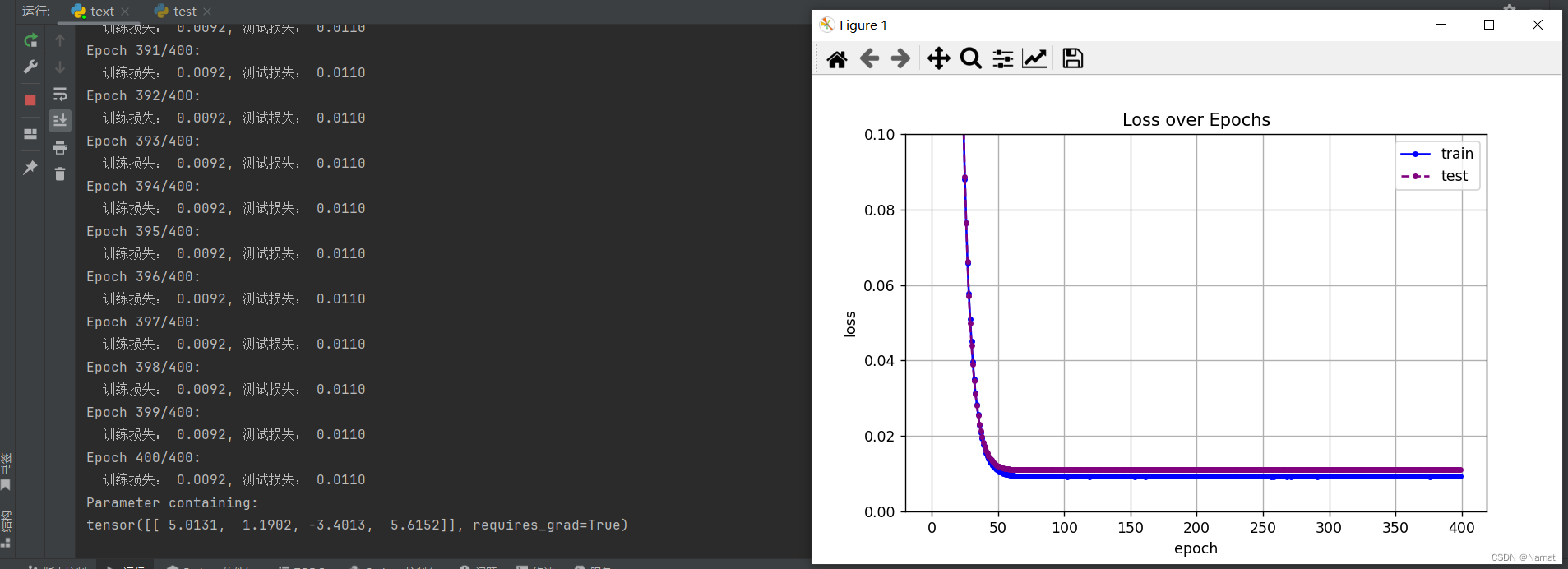
正常擬合的模型在損失到達最低點后便不再上升，訓練出來的模型與真實數據也及其接近

正常擬合才是我們訓練模型的期望狀態