
?個人主頁:?熬夜學編程的小林
💗系列專欄:?【C語言詳解】?【數據結構詳解】
目錄
1、浮點數在內存中的存儲
1.1、練習
1.2、浮點數怎么轉化為二進制
1.3、浮點數的存儲
1.3.1、浮點數存的過程
1.3.2、浮點數取的過程
1.3、題目解析
總結
1、浮點數在內存中的存儲
常見的浮點數:3.14159、1E10(1^10)等,浮點數家族包括: float 、 double 、 long double 類型。
浮點數表示的范圍: float.h 中定義
1.1、練習
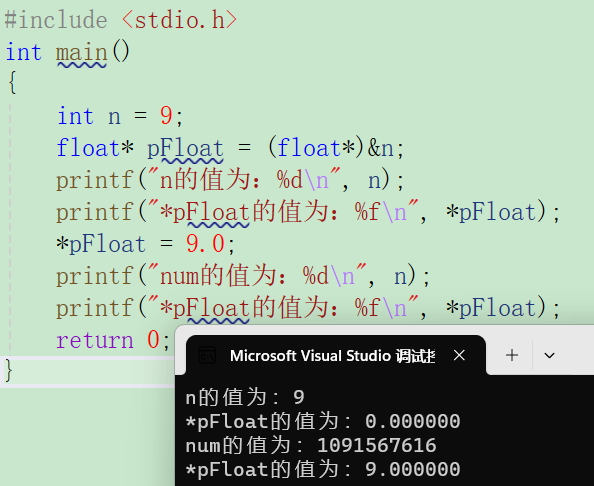
#include <stdio.h>
int main()
{int n = 9;float *pFloat = (float *)&n;printf("n的值為:%d\n",n);printf("*pFloat的值為:%f\n",*pFloat);*pFloat = 9.0;printf("num的值為:%d\n",n);printf("*pFloat的值為:%f\n",*pFloat);return 0;
}
輸出什么?
按照我們整數存儲的想法,打印的結果分別是9、9.000000、9、9.000000
但是為什么會出現上面的結果呢?下面就從浮點數的存儲來詳細講解此代碼。
1.2、浮點數怎么轉化為二進制
首先我們來個簡單的例子:
把十進制小數5.25化為二進制小數,我們應該怎么操作?
我們分為以下幾步:
1. 以小數點為界進行拆分;
2. 整數部分轉為二進制相信大家肯定沒問題
3. 小數部分采用的是"乘2取整法",當乘2之后小數部分得到0就停止計算
十進制小數5.25:
1、以小數點為界進行拆分,整數部分為5,小數部分為0.25
2、整數轉化為二進制為101
3、小數部分采取“乘2取整法”,0.25*2=0.5,整數部分為0,小數部分為0.5,繼續乘2,0.5*2=1.0,整數部分為1,小數部分為0,小數部分為0則停止計算。取的數字為整數部分數字,因此轉化為二進制小數為0.01。
4. 合并結果:整數部分 + 小數部分,最終得到二進制結果為101.01.
5. 二進制小數轉化為十進制驗算
101.01=1*2^2+0*2^1+1*2^0+0*2^-1+1*2^-2=5.25
以上就是浮點數化為二進制的步驟了,下面我們來看看更復雜一點的例子:
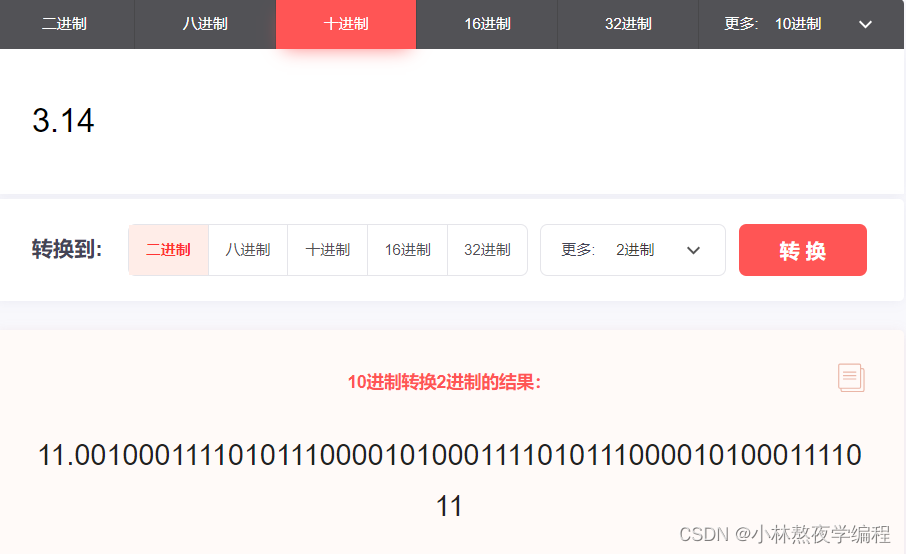
把十進制3.14化為二進制:
1、以小數點為界進行拆分,整數部分為3,小數部分為0.14
2、整數轉化為二進制為11
3、小數部分采取“乘2取整法”,0.14*2=0.28,整數部分為0,小數部分為0.28,繼續乘2, 0.28*2=0.56,整數部分為0,小數部分為0.56,繼續乘2, 0.56*2=1.12,整數部分為1,小數部分為0.12,繼續乘2, 0.12*2=0.24,整數部分為0,小數部分為0.24,.............小數部分為0則停止計算。取的數字為整數部分數字。
1.3、浮點數的存儲
上面的代碼中, num 和 *pFloat 在內存中明明是同?個數,為什么浮點數和整數的解讀結果會差別這么大?
要理解這個結果,?定要搞懂浮點數在計算機內部的表示方法。
根據國際標準IEEE(電氣和電子?程協會) 754,任意?個?進制浮點數V可以表示成下面的形式:
V ? = ?(?1) ^S *?M ? 2^E
? (?1)^S 表示符號位,當S=0,V為正數;當S=1,V為負數
? M 表示有效數字,M是大于等于1,小于2的
? 2^E 表示指數位
舉例來說:
?進制的5.0,寫成?進制是 101.0 ,相當于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
?進制的-5.0,寫成?進制是 -101.0 ,相當于 -1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754規定:
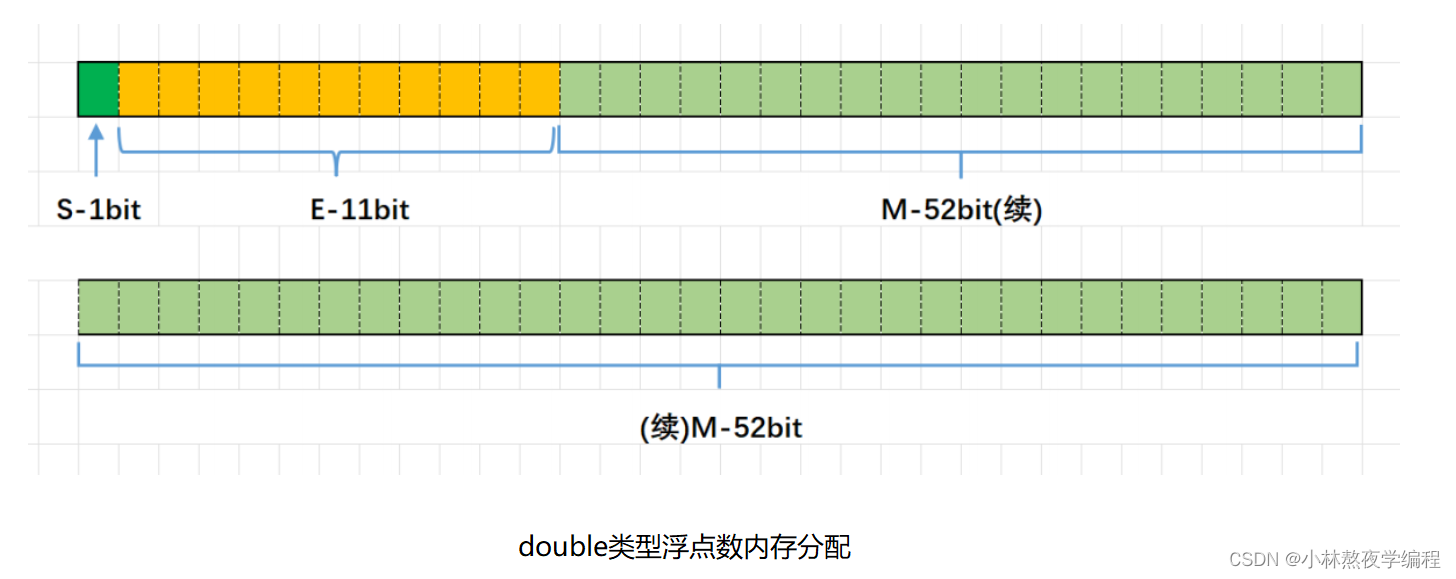
對于32位的浮點數,最高的1位(第一位)存儲符號位S,接著的8位存儲指數E,剩下的23位存儲有效數字M。
對于64位的浮點數,最高的1位(第一位)存儲符號位S,接著的11位存儲指數E,剩下的52位存儲有效數字M。
1.3.1、浮點數存的過程
IEEE 754 對有效數字M和指數E,還有?些特別規定。
前面說過, 1 ≤ M<2 ,也就是說,M可以寫成 1.xxxxxx 的形式,其中 xxxxxx 表示小數部分。
IEEE 754 規定,在計算機內部保存M時,默認這個數的第?位總是1,因此可以被舍去,只保存后面的 xxxxxx部分。比如保存1.01的時候,只保存01,等到讀取的時候,再把第?位的1加上去。這樣做的目的,是節省1位有效數字。以32位浮點數為例,留給M只有23位,將第?位的1舍去以后,等于可以保存24位有效數字。
至于指數E,情況就比較復雜。
首先,E為?個無符號整數(unsigned int)。
這意味著,如果E為8位,它的取值范圍為0~255;如果E為11位,它的取值范圍為0~2047。但是,我們知道,科學計數法中的E是可以出現負數的,所以IEEE 754規定, 存入內存時E的真實值必須再加上?個中間數 ,對于8位的E,這個中間數是127;對于11位的E,這個中間數是1023。比如,2^10的E是10,所以保存成32位浮點數時,必須保存成10+127=137,即10001001。
1.3.2、浮點數取的過程
指數E從內存中取出還可以再分成三種情況:
E不全為0或不全為1
這時,浮點數就采用下面的規則表示,即 指數E的計算值減去127(或1023) ,得到真實值,再將 有效數字M前加上第?位的1。
比如:0.5 的?進制形式為0.1,由于規定正數部分必須為1,即將小數點右移1位,則為1.0*2^(-1),其階碼為-1+127(中間值)=126,表示為01111110,而尾數1.0去掉整數部分為0,補齊0到23位 00000000000000000000000,則其?進制表示形式為:
0 01111110 00000000000000000000000
E全為0
這時,浮點數的指數E等于1-127(或者1-1023)即為真實值,有效數字M不再加上第?位的1,而是還原為0.xxxxxx的小數。這樣做是為了表示±0,以及接近于0的很小的數字。
0 00000000 00100000000000000000000
E全為1
這時,如果有效數字M全為0,表示±無窮大(正負取決于符號位s);
0 11111111 00010000000000000000000
好了,關于浮點數的表示規則,就說到這里。
1.3、題目解析
下面,讓我們回到?開始的練習
先看第1環節,為什么 9 還原成浮點數,就成了 0.000000 ?
9以整型的形式存儲在內存中,得到如下?進制序列:
0000 0000 0000 0000 0000 0000 0000 1001
首先,將 9 的?進制序列按照浮點數的形式拆分,得到第?位符號位s=0,后面8位的指數
E=00000000 , 最后23位的有效數字M=000 0000 0000 0000 0000 1001。
由于指數E全為0,所以符合E為全0的情況。因此,浮點數V就寫成:
V=(-1)^0 × 0.00000000000000000001001×2^(-126)=1.001×2^(-146)
顯然,V是?個很小的接近于0的正數,所以用十進制小數表示就是0.000000。
再看第2環節,浮點數9.0,為什么整數打印是 1091567616?
首先,浮點數9.0 等于?進制的1001.0,即換算成科學計數法是:1.001×2^3
所以: 9.0? = ?(?1) ^0?? (1.001)? ? ?2^3
那么,第?位的符號位S=0,有效數字M等于001后面再加20個0,湊滿23位,指數E等于3+127=130, 即10000010
所以,寫成?進制形式,應該是S+E+M,即
0 10000010 001 0000 0000 0000 0000 0000
這個32位的?進制數,被當做整數來解析的時候,就是整數在內存中的補碼,此數為正數,原反補碼相同,原碼正是 1091567616 。
通過浮點數進行存儲,按照浮點數打印,因此*pFloat=9.000000。
總結
本篇博客就結束啦,謝謝大家的觀看,如果公主少年們有好的建議可以留言喔,謝謝大家啦!





無人機三維路徑規劃,輸出做短路徑圖和適應度曲線。)










)




)

