曲線擬合
No.1
什么是曲線擬合
所謂的曲線擬合,就是使用某一個模型(或者稱為方程式),將一系列的數據擬成平滑的曲線,以便觀察兩組數據之間的內在聯系,了解數據之間的變化趨勢。
No.2
曲線擬合的應用
在數據分析時,我們有時需要通過已有數據來預測未來數據。在一些復雜的數據模型中,數據維度很多,數據之間的關系很復雜,我們可能會用到深度學習的算法。但是在一些簡單的數據模型中,數據之間有很明顯的相關性,那我們就可以使用簡單的曲線擬合來預測未來的數據。
No.3
模型的優化
根據模型的建立與求解的過程中, 發現擬合的函數表達式有很多, 即使根據可決系數, 顯著性檢驗和系數值穩定等條件, 依然會出現多個表達式。那么這種情況是要選擇優化數據和處理, 根據實際情況而處理。函數表達式的系數也決定了函數的靈敏度, 選擇原則在不同的問題中根據數據最終結果來處理。
No.4
曲線擬合的方法
Excel曲線工具
假設我們有一組用戶生命周期價值(LTV)和天數的對應數據
DayLTV1$0.202$0.353$0.454$0.525$0.576$0.607$0.628$0.63
將數據放進Excel中,插入折線圖
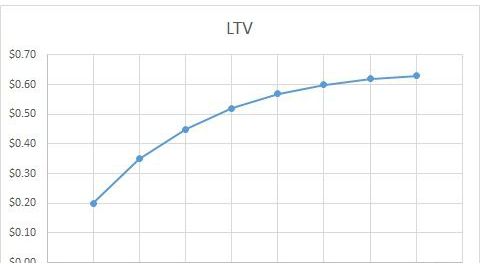
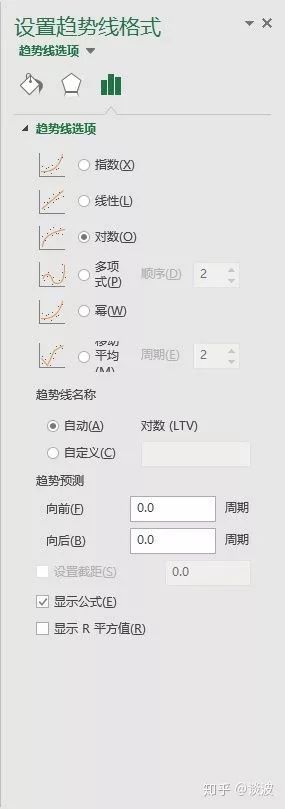
右擊藍色曲線,選擇“添加趨勢線”,并選擇趨勢線為“對數”,并勾選“顯示公式”
可以看到,曲線圖中出現了一條虛線的曲線,并顯示了對應的公式為
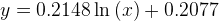
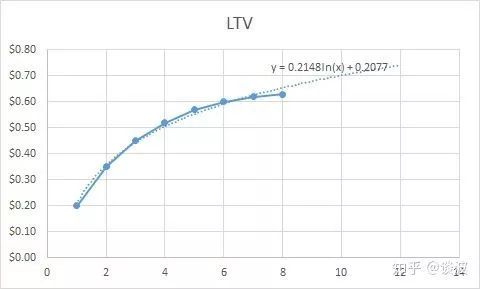
Excel的趨勢線工具提供了幾個常用的函數,包括指數函數、對數函數等,可以滿足一般需求。但是如果數據曲線相對復雜的話,就需要用到下面的工具了。
介紹一個非常好用的在線曲線擬合工具:
http://www.qinms.com/webapp/curvefit/cf.aspx
No.5
Python matplotlib庫
Python的matplotlib庫有一個自定義公式來擬合曲線的功能。下面代碼演示了通過它來擬合上述例子的過程
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import scipy.optimize as optimization
data_day = [1,2,3,4,5,6,7,8] #x坐標值|x coord
data_ltv = [0.2,0.35,0.45,0.52,0.57,0.6,0.62,0.63] #y坐標值|y coord
xdata = np.array(data_day)
ydata = np.array(data_ltv)
#定義使用的公式|customize equation
def lnFunction(x, A, B):
????return A*np.log(x)+B
guess = [1, 1] ?#定義初始A、B|initialize a and b
try:
????params, params_covariance = optimization.curve_fit(lnFunction, xdata, ydata, guess) #擬合,A、B結果存入params|curve fitting and store a, b values to params
????print params
????result = '' #輸出結果|to store result
????for i in range(1, 15):
?result += str(round(lnFunction(i, params[0], params[1]), 2)) ???#將i帶入公式中的x,使用擬合出的A、B值計算y值,并保留兩位小數|calculate result for each i as x using the a, b values, and round the result to 2 points
????????if i != 14:
????????????result += ',' ??#每個結果用逗號隔開,并省略最后一個逗號|separate each result with comma, and omit the last comma
????print result
except:
????print ''
輸出結果為:
[0.21482987 0.20772681]
0.21,0.36,0.44,0.51,0.55,0.59,0.63,0.65,0.68,0.7,0.72,0.74,0.76,0.77
No.6
曲線擬合公式
在前面的例子中,我們使用了對數函數來進行擬合。在上文提到的在線曲線擬合工具網站中,也列出了一些常見的擬合方程,包括直線、多項式、對數、指數等。其中有一個方程對于擬合自然曲線非常好用,就是四參數方程。
四參數方程的格式為:
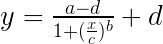
最后
統計學作為一門新興的學科, 在未來的社會發展中有著舉足輕重的意義。擬合方法是一種可以很好的查看出數據趨勢的一種方法,同樣也可以用在數據近似,差值等方法中。使得數學建模的操作增添新的工具, 極大地提高了數據分析的科學性。


文案:競賽部 董聿銘
排版:張添嬌 高歆然
審核:由? ? 月?李天嬌





服務控制及優化啟動過程)













