


文章發布于公號【數智物語】 (ID:decision_engine),關注公號不錯過每一篇干貨。
來源 | SAMshare(id:SAMshare)
作者 | samshare

"本次主要講解的內容就是特征降維,主要涉及PCA以及一些常見分析方法。"
01
Index
一,PCA降維算法
1. 內積與投影
2. 基與基變換
3. 方差
4. 協方差
5. 協方差矩陣
6. 協方差矩陣對角化
7. PCA算法步驟
8. PCA實例
9. PCA的Python操作
二,LDA降維算法
1. LDA介紹
2. LDA的優缺點
3. LDA的Python操作
在機器學習中,我們有的時候會遇到維度災難,當模型的訓練入參有很多的時候,往往是需要很多的時間和資源去訓練的,而這不是我們想要看到的結果。一般情況下,我們都是會對源數據進行特征處理,提取對預測更加有效的特征。
有的時候,我們會得到比較高維的特征向量,而這里面往往包含很多的噪聲與冗余數據,所以我們需要通過降維的方式去獲取特征更加有效的信息,一來提高特征表達能力,二來提高模型訓練的效率。
02
PCA降維算法
PCA(Principal Components Analysis),即主成分分析,是降維操作中最經典的方法,它是一種線性的、無監督、全局性的降維算法,旨在找到數據中的"主要成分",提取主成分從而達到降維的目的。PCA是一種無監督算法,也就是我們不需要標簽也能對數據做降維,這就使得其應用范圍更加廣泛了,但是PCA也有一個問題,原來的數據中比如包括了年齡,性別,身高等指標降維后的數據既然維度變小了,那么每一維都是什么含義呢?這個就很難解釋了,所以PCA本質來說是無法解釋降維后的數據的物理含義。
在了解PCA之前,有一些基礎的名詞需要溫習一下:
01
內積與投影
內積運算將兩個向量映射為一個實數,下面是兩個維數相同的向量的內積:
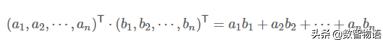
假設存在兩個點A,B,其在坐標軸的位置如下圖:
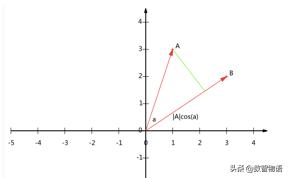
我們從A向B引一條垂線,也就是A在B上的投影,其夾角為a,則投影的矢量長度為|A|cos(a),其中
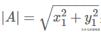
是向量A的模,也就是A線段的標量長度。
而內積的另一種表現形式為:

也就是說,當B的模為1的時候,也就是單位向量的時候,內積可以表示為:
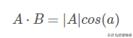
也就是A與B的內積值等于A向B所在直線投影的矢量長度。
02
基與基變換
基可以理解為單位向量,基都是正交的(即內積為0,直觀來說就是相互垂直),并且是線性無關的。
基變換指的是當前向量和一個基進行內積運算,得到的結果作為新的坐標分量。
假設存在一個點(3,2),一般我們都會取(1,0)和(0,1)為基,也就是我們的X和Y軸方向。如果我們取(1,1)和(-1,1)為我們的基,但我們希望基的模為1,這樣子會方便計算,所以可以除以當前的模長,所以上面的基就變成了:

如下圖所示:
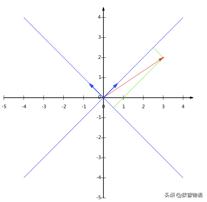
所以,進行基變換,只需要進行一次內積運算:
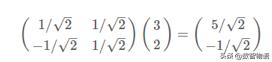
03
方差
一個字段的方差可以看做是每個元素與字段均值的差的平方和的均值,即:
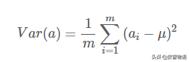
一般我們都會把均值為化為0,即進行一次變換,所以方差可以表示為:
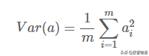
04
協方差
如果單純地選擇方差最大的方向,則無法保證兩個字段之間相互獨立,因為我們需要的是盡可能多地保留原始信息,但又是相互獨立,這里我們引入一下概念,協方差,用來表示兩個字段的相關性,公式為:
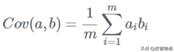
協方差:度量各個維度偏離其均值的程度。協方差的值如果為正值,則說明兩者是正相關的(從協方差可以引出“相關系數”的定義),結果為負值就說明負相關的,如果為0,也是就是統計上說的“相互獨立”。
所以,我們的目標就是讓兩個字段的協方差為0,為了協方差為0,選擇第二個基的時候,必須要在第一個基的正交方向上選擇。
我們說的PCA降維,就是把N維的特征,降到K維(0 < K < N),也就是說要選擇k個單位正交基,并且盡可能讓方差最大化。
05
協方差矩陣
在統計學與概率論中,協方差矩陣的每個元素是各個向量元素之間的協方差,是從標量隨機變量到高維度隨機向量的自然推廣。
假設存在矩陣X:
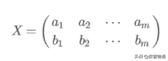
其協方差矩陣為:
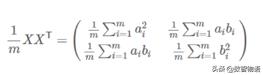
可以看出,協方差矩陣的對角線元素為兩個字段的方差,而其他元素為矩陣的協方差,按照我們之前的說法,我們需要得到協方差為0,并且方差最大的轉換。
06
協方差矩陣對角化
根據上述推導,我們發現要達到優化目前,等價于將協方差矩陣對角化:即除對角線外的其它元素化為0,并且在對角線上將元素按大小從上到下排列,這樣我們就達到了優化目的。這樣說可能還不是很明晰,我們進一步看下原矩陣與基變換后矩陣協方差矩陣的關系。
設原始數據矩陣X對應的協方差矩陣為C,而P是一組基按行組成的矩陣,設Y=PX,則Y為X對P做基變換后的數據。設Y的協方差矩陣為D,我們推導一下D與C的關系:
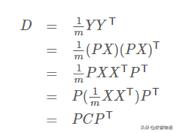
我們要找的P不是別的,而是能讓原始協方差矩陣對角化的P。換句話說,優化目標變成了尋找一個矩陣P,滿足PCP^T是一個對角矩陣,并且對角元素按從大到小依次排列,那么P的前K行就是要尋找的基,用P的前K行組成的矩陣乘以X就使得X從N維降到了K維并滿足上述優化條件。
07
PCA算法步驟
設有mXn維數據。
1)將原始數據按列組成n行m列矩陣X
2)將X的每一行(代表一個屬性字段)進行零均值化,即減去這一行的均值
3)求出協方差矩陣C=1mXXT
4)求出協方差矩陣的特征值及對應的特征向量
5)將特征向量按對應特征值大小從上到下按行排列成矩陣,取前k行組成矩陣P
6)Y=PX即為降維到k維后的數據
08
PCA實例
假設存在2維數據

:,需要將其降至1維。
1)均值歸0:目前每個維度的均值均為0,無需變換。
2)求協方差矩陣
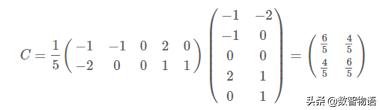
3)求解特征值以及特征向量
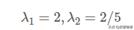
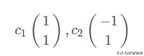
可以參考:https://jingyan.baidu.com/article/27fa7326afb4c146f8271ff3.html
4)標準化特征向量
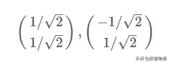
5)得到對角矩陣P并驗證對角化
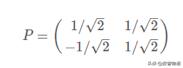
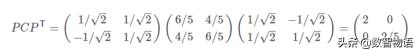
6)因為需要得到1維矩陣,因此用P的第一行乘以原矩陣即可:
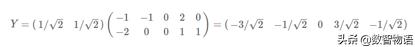
降維投影如下圖所示:
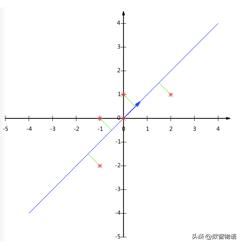
09
Python操作
# 使用sklearn進行PCA降維import numpy as npfrom sklearn.decomposition import PCAX = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]]) #導入數據,維度為4print('原矩陣X:', X)pca = PCA(n_components=2) #降到2維pca.fit(X) #訓練newX=pca.fit_transform(X) #降維后的數據print('貢獻率:', pca.explained_variance_ratio_)print('降維后矩陣:', newX)'''參數解釋:n_components: 我們可以利用此參數設置想要的特征維度數目,可以是int型的數字,也可以是閾值百分比,如95%,讓PCA類根據樣本特征方差來降到合適的維數,也可以指定為string類型,MLE。copy:bool類型,TRUE或者FALSE,是否將原始數據復制一份,這樣運行后原始數據值不會改變,默認為TRUE。whiten:bool類型,是否進行白化(就是對降維后的數據進行歸一化,使方差為1),默認為FALSE。如果需要后續處理可以改為TRUE。explained_variance_: 代表降為后各主成分的方差值,方差值越大,表明越重要。explained_variance_ratio_: 代表各主成分的貢獻率。inverse_transform(): 將降維后的數據轉換成原始數據,X=pca.inverse_transform(newX)。'''output:

03
LDA降維算法
線性判別分析(Linear Discriminant Analysis,LDA)是一種有監督學習算法,也是經常被拿來降維,它和PCA的區別在于是否存在標簽,其中心思想就是—— 最大化類間距離和最小化類內距離。
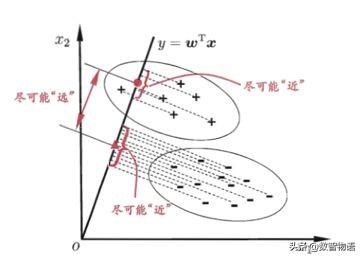
而PCA的不足在于不能很好地分開不同類別的數據,如下圖:
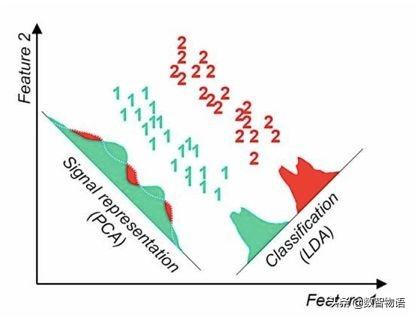
LDA算法既可以用來降維,又可以用來分類,但是目前來說,主要還是用于降維。在我們進行圖像識別圖像識別相關的數據分析時,LDA是一個有力的工具。下面總結下LDA算法的優缺點:
01
優點:
1)在降維過程中可以使用類別的先驗知識經驗,而像PCA這樣的無監督學習則無法使用類別先驗知識。
2)LDA在樣本分類信息依賴均值而不是方差的時候,比PCA之類的算法較優。
02
缺點:
1)LDA不適合對非高斯分布樣本進行降維,PCA也有這個問題。
2)LDA降維最多降到類別數k-1的維數,如果我們降維的維度大于k-1,則不能使用LDA。當然目前有一些LDA的進化版算法可以繞過這個問題。
3)LDA在樣本分類信息依賴方差而不是均值的時候,降維效果不好。
4)LDA可能過度擬合數據。
03
Python操作
import numpy as npfrom sklearn.discriminant_analysis import LinearDiscriminantAnalysisX = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])y = np.array([1, 1, 1, 2, 2, 2])clf = LinearDiscriminantAnalysis()clf.fit(X, y) LinearDiscriminantAnalysis(n_components=None, priors=None, shrinkage=None, solver='svd', store_covariance=False, tol=0.0001)print(clf.predict([[-0.8, -1]]))04
Reference
1)Reference十分鐘搞定PCA主成分分析
https://blog.csdn.net/tangyudi/article/details/80188302#comments
2)PCA的數學原理
http://blog.codinglabs.org/articles/pca-tutorial.html


星標我,每天多一點智慧




![[算法]淺談求n范圍以內的質數(素數)](http://pic.xiahunao.cn/[算法]淺談求n范圍以內的質數(素數))




的調用詳解)






考試 全國各省市成績查詢)


