關于InnoDB索引,我們可能知道InnDB索引是用B+樹實現的,而B+樹就是一種能優化查詢速度的數據結構。但我們又沒想過這樣一個問題,能優化查詢速度的數據結構有很多,為什么InnoDB要采用B+樹?
常見優化查詢速度數據結構
哈希表
哈希表是一種以鍵 - 值(key-value)存儲數據的結構,我們只要輸入待查找的鍵即 key,就可以找到其對應的值即 Value。哈希的思路很簡單,把值放在數組里,用一個哈希函數把 key 換算成一個確定的位置,然后把 value 放在數組的這個位置。
不可避免地,多個 key 值經過哈希函數的換算,會出現同一個值的情況。處理這種情況的一種方法是,拉出一個鏈表。
假設現在維護著一個身份證信息和姓名的表,需要根據身份證號查找對應的名字,這時對應的哈希索引的示意圖如下所示:
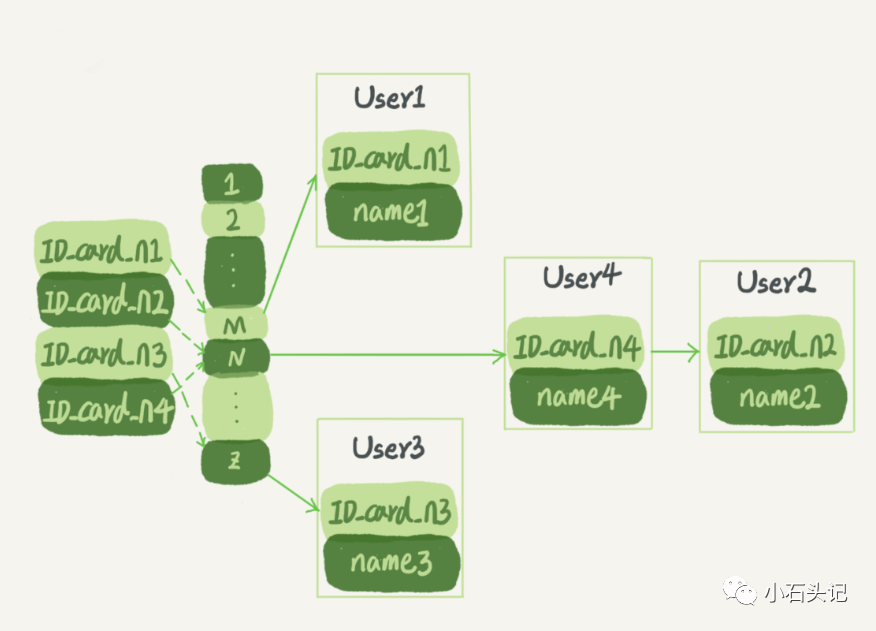
圖中,User2 和 User4 根據身份證號算出來的值都是 N,但沒關系,后面還跟了一個鏈表。假設,這時候你要查 IDcardn2 對應的名字是什么,處理步驟就是:首先,將 IDcardn2 通過哈希函數算出 N;然后,按順序遍歷,找到 User2。
需要注意的是,圖中四個 IDcardn 的值并不是遞增的,這樣做的好處是增加新的 User 時速度會很快,只需要往后追加。但缺點是,因為不是有序的,所以哈希索引做區間查詢的速度是很慢的。
可以設想下,如果現在要找身份證號在[IDcardX, IDcardY]這個區間的所有用戶,就必須全部掃描一遍了。
所以,哈希表這種結構適用于只有等值查詢的場景,比如 Memcached 及其他一些 NoSQL 引擎。
有序數組
有序數組在等值查詢和范圍查詢場景中的性能就都非常優秀。還是上面這個根據身份證號查名字的例子,如果我們使用有序數組來實現的話,示意圖如下所示:
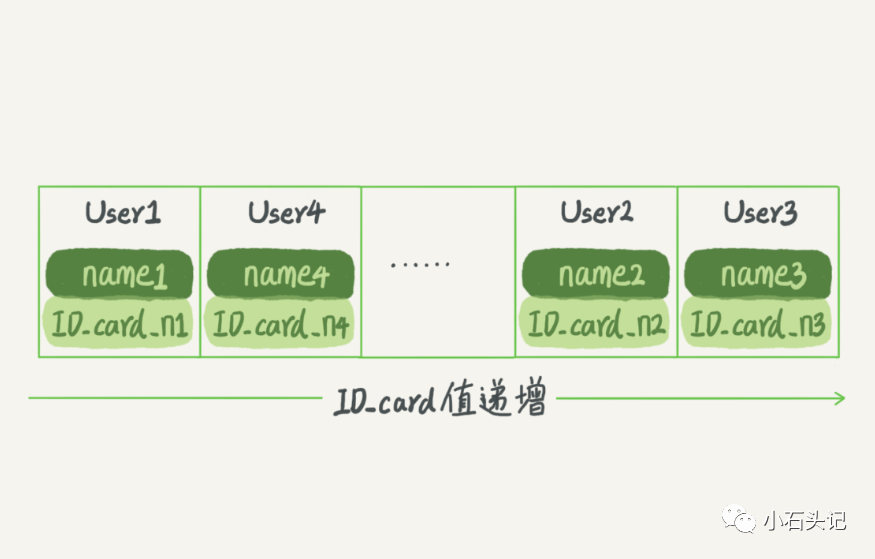
這里我們假設身份證號沒有重復,這個數組就是按照身份證號遞增的順序保存的。這時候如果你要查 IDcardn2 對應的名字,用二分法就可以快速得到,這個時間復雜度是 O(log(N))。
同時很顯然,這個索引結構支持范圍查詢。要查身份證號在[IDcardX, IDcardY]區間的 User,可以先用二分法找到 IDcardX(如果不存在 IDcardX,就找到大于 IDcardX 的第一個 User),然后向右遍歷,直到查到第一個大于 IDcardY 的身份證號,退出循環。
如果僅僅看查詢效率,有序數組就是最好的數據結構了。但是,在需要更新數據的時候就麻煩了,往中間插入一個記錄就必須得挪動后面所有的記錄,成本太高。
所以,有序數組索引只適用于靜態存儲引擎,比如要保存的是 2017 年某個城市的所有人口信息,這類不會再修改的數據。
二叉搜索樹
上面根據身份證號查名字的例子,如果我們用二叉搜索樹來實現的話,示意圖如下所示:
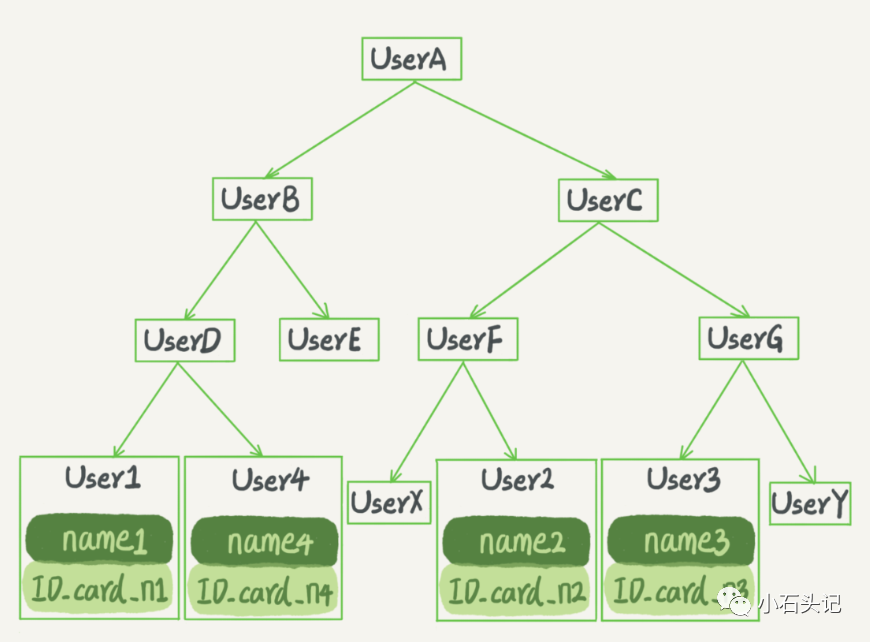
二叉搜索樹的特點是:每個節點的左兒子小于父節點,父節點又小于右兒子。這樣如果你要查 IDcardn2 的話,按照圖中的搜索順序就是按照 UserA -> UserC -> UserF -> User2 這個路徑得到。這個時間復雜度是 O(log(N))。
當然為了維持 O(log(N)) 的查詢復雜度,就需要保持這棵樹是平衡二叉樹。為了做這個保證,更新的時間復雜度也是 O(log(N))。
樹可以有二叉,也可以有多叉。多叉樹就是每個節點有多個兒子,兒子之間的大小保證從左到右遞增。二叉樹是搜索效率最高的,但是實際上大多數的數據庫存儲卻并不使用二叉樹。其原因是,索引不止存在內存中,還要寫到磁盤上。
可以想象一下一棵 100 萬節點的平衡二叉樹,樹高 20。一次查詢可能需要訪問 20 個數據塊。在機械硬盤時代,從磁盤隨機讀一個數據塊需要 10 ms 左右的尋址時間。也就是說,對于一個 100 萬行的表,如果使用二叉樹來存儲,單獨訪問一個行可能需要 20 個 10 ms 的時間,這個查詢可真夠慢的。
為了讓一個查詢盡量少地讀磁盤,就必須讓查詢過程訪問盡量少的數據塊。那么,我們就不應該使用二叉樹,而是要使用“N 叉”樹。這里,“N 叉”樹中的“N”取決于數據塊的大小。
以 InnoDB 的一個整數字段索引為例,這個 N 差不多是 1200。這棵樹高是 4 的時候,就可以存 1200 的 3 次方個值,這已經 17 億了。考慮到樹根的數據塊總是在內存中的,一個 10 億行的表上一個整數字段的索引,查找一個值最多只需要訪問 3 次磁盤。其實,樹的第二層也有很大概率在內存中,那么訪問磁盤的平均次數就更少了。
N 叉樹由于在讀寫上的性能優點,以及適配磁盤的訪問模式,已經被廣泛應用在數據庫引擎中了。
數據庫引擎常用數據結構
B樹
B樹也稱B-樹,它是一顆多路平衡查找樹,B樹和后面講到的B+樹也是從最簡單的二叉樹變換而來的,并沒有什么神秘的地方,下面我們來看看B樹的定義。
每個節點最多有m-1個關鍵字(可以存有的鍵值對)。
根節點最少可以只有1個關鍵字。
非根節點至少有m/2個關鍵字。
每個節點中的關鍵字都按照從小到大的順序排列,每個關鍵字的左子樹中的所有關鍵字都小于它,而右子樹中的所有關鍵字都大于它。
所有葉子節點都位于同一層,或者說根節點到每個葉子節點的長度都相同。
每個節點都存有索引和數據,也就是對應的key和value。
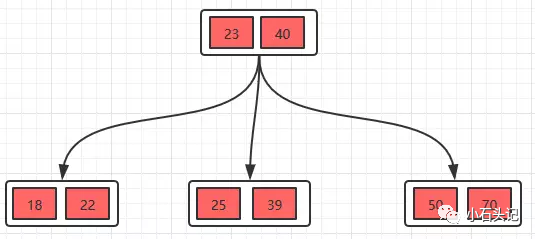
B+樹
B+樹其實和B樹是非常相似的,我們首先看看相同點。
相同點:?根節點至少一個元素 非根節點元素范圍:m/2 <= k <= m-1
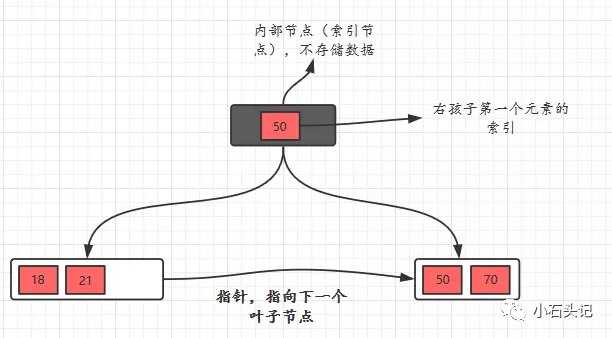
不同點:?B+樹有兩種類型的節點:內部結點(也稱索引結點)和葉子結點。內部節點就是非葉子節點,內部節點不存儲數據,只存儲索引,數據都存儲在葉子節點。內部結點中的key都按照從小到大的順序排列,對于內部結點中的一個key,左樹中的所有key都小于它,右子樹中的key都大于等于它。葉子結點中的記錄也按照key的大小排列。?每個葉子結點都存有相鄰葉子結點的指針,葉子結點本身依關鍵字的大小自小而大順序鏈接。?父節點存有右孩子的第一個元素的索引。
總結
B和B+樹的區別在于,B+樹的非葉子結點只包含導航信息,不包含實際的值,所有的葉子結點和相連的節點使用鏈表相連,便于區間查找和遍歷。
B+ 樹的優點在于:
由于B+樹在內部節點上不包含數據信息,因此在內存頁中能夠存放更多的key。數據存放的更加緊密,具有更好的空間局部性。因此訪問葉子節點上關聯的數據也具有更好的緩存命中率。
B+樹的葉子結點都是相鏈的,因此對整棵樹的便利只需要一次線性遍歷葉子結點即可。而且由于數據順序排列并且相連,所以便于區間查找和搜索。而B樹則需要進行每一層的遞歸遍歷。相鄰的元素可能在內存中不相鄰,所以緩存命中性沒有B+樹好。
但是B樹也有優點,其優點在于,由于B樹的每一個節點都包含key和value,因此經常訪問的元素可能離根節點更近,因此訪問也更迅速。
往期推薦
深入學習G1垃圾收集器
Redisson分布式鎖自動續期源碼分析
spring中發布訂閱模式實踐








:安裝JDK)










