題目描述

A Light-Emitting Diode (LED) is a semiconductor light source, which emits light when an electric current of voltage higher than a threshhold is applied to its leads. ACM R&D recently reported that they have succesfully developed a new LED, namely, ACMOLED. An ACMOLED has a special behavior that the intensity of light emitted from it changes in two steps as the voltage of the electric current increases, as depicted in the graph below.

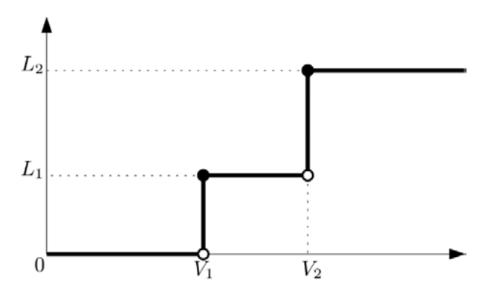
As shown, an ACMOLED is not activated in the voltage range from 0 to V1, while it emits light with intensity L1 ≥ 0 when the voltage reaches the first threshold V1 and light with intensity L2 ≥ L1 when the voltage reaches the x threshold V2. More specifically, if F(v) is the function that maps voltage v to the intensity of light emitted from an ACMOLED, then for four real numbers L1, L2, V1, and V2 with 0 ≤ L1 ≤ L2 and 0 < V1 < V2, we have

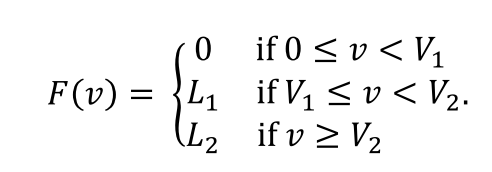
The very issue now is that ACM R&D still does not know the exact values of two threshold voltage values V1 and V2 and the two intensity values L1 and L2 as well. Researchers in ACM R&D plan to estimate these four values for ACMOLEDs by repeated experiments.
Experiments are performed by applying current of a specific voltage and observing the intensity of light emitted from an ACMOLED. After n repeated experiments with different voltage values, obtained are the data of n tuples (v1, l1), (v2, l2), ..., (vn, ln), where li is the observed intensity for voltage vi. Due to the impreciseness of the observing device and other reasons, the experimental data are not accurate and may contain some error. Nonetheless, they want to find a best estimated intensity function F(v) that minimizes the following error function:

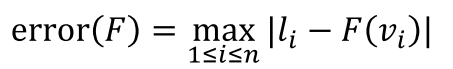
where |x| denotes the absolute value of a real number x.
For a given data of n tuples, write a program that finds an estimated intensity function F that minimizes the above error function and outputs the value of error(F).

?

輸入

Your program is to read from standard input. The input starts with a line containing an integer n (1 ≤ n ≤ 300,000), where n is the number of tuples (vi, li) in the experimental data. In the following n lines, each line contains two integers, which range inclusively from 0 to 109, representing vi and li in each tuple (vi, li) of the experimental data. Note that you may assume that there are no two tuples (vi, li) and (vj, lj) in the input such that 1 ≤ i < j ≤ n and vi = vj.

?

輸出

Your program is to write to standard output. Print exactly one line consisting of one real number, rounded to the first decimal place, which represents the minimum value of error(F).

?

樣例輸入

復制樣例數據

5
0 0
2 1
3 5
6 7
7 11

樣例輸出

1.0

題目大意：

此題大體上就是在第一象限內給出n個點，輸入第一行為n，下面n行為這n個點的坐標，現在要找出一個函數，形如圖中給的階梯型，要使的這些點到這個分段階梯的距離的最大值最小化，并求出這個最小化的最大值。

解題思路：

此題是一道二分的題，我們可以通過二分點的誤差范圍，通過判斷是否可以由這樣三條直線來構成，來確定二分的條件，但需要注意的是，若第一個點的橫坐標為0，即其在y軸上時，需要將左邊界改為此時點的y值，因為此時這個點一定是落在第一條線段上的。

代碼：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <bitset>
#include <set>
#include <utility>
#include <sstream>
#include <iomanip>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define inf 0x3f3f3f3f
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define lep(i,l,r) for(int i=l;i>=r;i--)
#define ms(arr) memset(arr,0,sizeof(arr))
//priority_queue<int,vector<int> ,greater<int> >q;
const int maxn = (int)1e5 + 5;
const ll mod = 1e9+7;
struct node
{double x,y;double up,down;
}arr[300100];
bool cmp(node a,node b) {return a.x<b.x;
}
int n;
bool judge(double d) {int t;rep(i,1,n) {if(arr[i].y-d>0) {     //將能放在第一條線段上的的點先去掉，即放在x軸上的t=i;break;}}int num=1;double up=arr[t].y+d,down=arr[t].y-d;for(int i=t+1;i<=n;i++) {if(arr[i].y+d<down) {       //此時不滿足情況，即當前的點在線段下面了return false;}else if(arr[i].y-d>up) {      //當前的點在此時線段渠道的范圍之上，需開一條新的線段num++;if(num>2) return false;up=arr[i].y+d;          //更新線段所在的區間down=arr[i].y-d;}else {up=min(up,arr[i].y+d);      //縮小線段所在的區間down=max(down,arr[i].y-d);}}return true;
}
int main() 
{#ifndef ONLINE_JUDGEfreopen("in.txt", "r", stdin);#endif//freopen("out.txt", "w", stdout);ios::sync_with_stdio(0),cin.tie(0);scanf("%d",&n);double maxy=-1;rep(i,1,n) {scanf("%lf %lf",&arr[i].x,&arr[i].y);maxy=max(maxy,arr[i].y);}sort(arr+1,arr+1+n,cmp);double l=0,r=maxy;if(arr[1].x==0) l=arr[1].y;while(r-l>0.00001) {double mid=(l+r)/2.0;if(judge(mid)) {r=mid;}else l=mid;}printf("%.1f\n",r);return 0;
}

?