遞歸函數

遞歸

遞歸就是一個函數在它的函數體內調用它自身。執行遞歸函數將反復調用其自身，每調用一次就進入新的一層。遞歸函數必須有結束條件。
當函數在一直遞推，直到遇到墻后返回，這個墻就是結束條件。
所以遞歸要有兩個要素，結束條件與遞推關系

注:

遞歸的時候，每次調用一個函數，計算機都會為這個函數分配新的空間，這就是說，當被調函數返回的時候，調用函數中的變量依然會保持原先的值，否則也不可能實現反向輸出。

例題

1. 計算n的階乘

#include <stdio.h> 
int factorial(int n)
{int result;if (n<0)                                          //判斷例外{printf("輸入錯誤!\n");return 0;} else if (n==0 || n==1){result = 1;  //回推墻}else{result = factorial(n-1) * n;  //遞推關系，這個數與上一個數之間的關系。}return result;
}int main(){int n = 5;                                              //輸入數字5，計算5的階乘printf("%d的階乘=%d",n,factorial(n));return 0;
}

程序在計算5的階乘的時候，先執行遞推，當n=1或者n=0的時候返回1，再回推將計算并返回。由此可以看出遞歸函數必須有結束條件。

2. 斐波那契數列

斐波那契數列指的是這樣一個數列:

0, 1, 1, 2, 3, 5, 8, 13, 21, ···

這個數列從第三項開始,每一項都等于前兩項之和.

#include <stdio.h>long fibonacci( long num )
{if ( num == 0 || num == 1 ){return num;}else{return fibonacci( num -1 ) + fibonacci( num -2 );}
}void main()
{long number;puts("請輸入一個正整數: ");scanf("%ld", &number);printf("斐波那契數列第%ld項為: %ld\n", number, fibonacci( number ) );}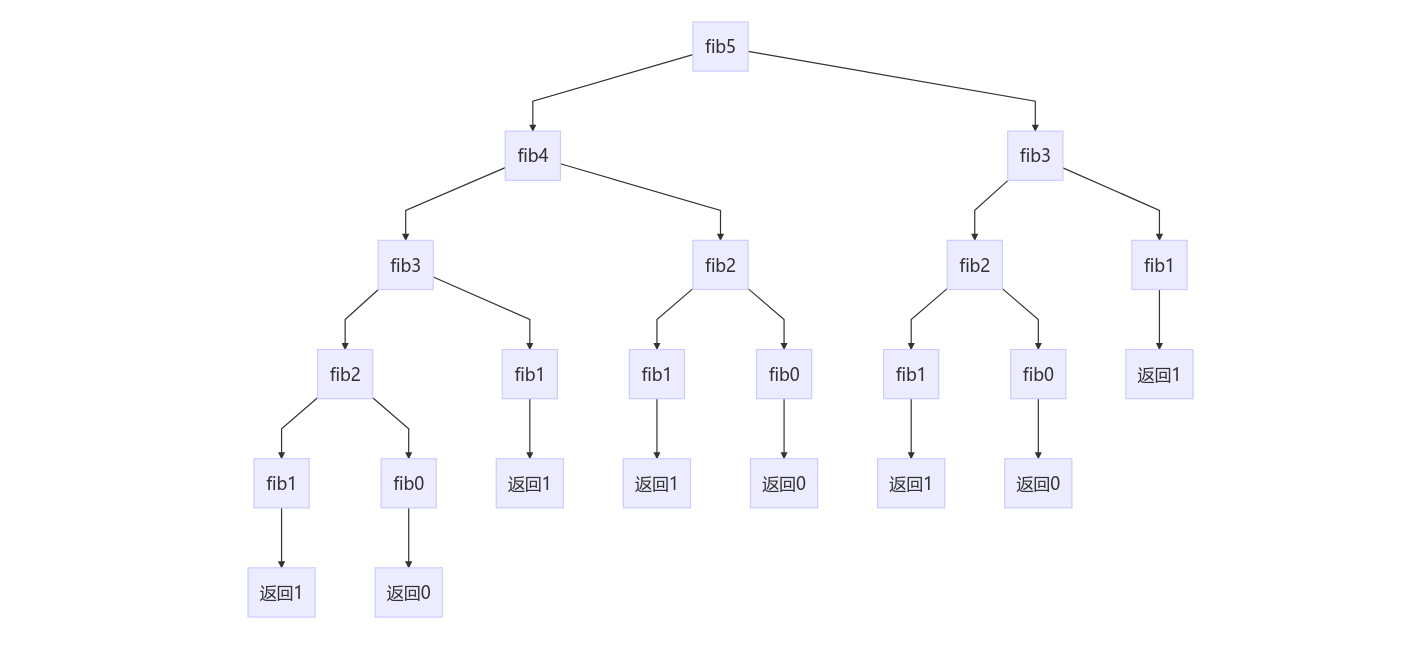

3. 應用題~~

小明為了學好英語，需要每天記單詞，第一天記1個，第二天記2個依次類推，請用代碼完成，算出小明第10天開始的時候會了多少個單詞？

分析：
墻(結束條件)是“第一天記1個”
遞推關系是“第n天記的單詞= 第n-1天記的單詞數量+n"

#include <stdio.h>
/* 定義獲取單詞數量的函數 */
int getWordNumber(n)
{   if(n == 1){return 1;    //回推墻}else{return getWordNumber(n-1)+n ;       //遞推關系}
}
int main()
{int num = getWordNumber(10);     //獲取會了的單詞數量printf("小明第10天記了:%d個單詞。\n", num);return 0;
}

特點

遞歸函數特點：

1. 每一級函數調用時都有自己的變量，但是函數代碼并不會得到復制，如計算5的階乘時每遞推一次變量都不同；
2. 每次調用都會有一次返回，如計算5的階乘時每遞推一次都返回進行下一次；
3. 遞歸函數中，位于遞歸調用前的語句和各級被調用函數具有相同的執行順序；
4. 遞歸函數中，位于遞歸調用后的語句的執行順序和各個被調用函數的順序相反；
5. 遞歸函數中必須有終止語句。

一句話總結遞歸：自我調用且有完成狀態。

效率

1. 系統棧（也叫核心棧、內核棧）
   是內存中屬于操作系統空間的一塊區域，其主要用途為： (1)保存中斷現場，對于嵌套中斷，被中斷程序的現場信息依次壓入系統棧，中斷返回時逆序彈出； (2)保存操作系統子程序間相互調用的參數、返回值、返回點以及子程序(函數)的局部變量。

2. 用戶棧
   是用戶進程空間中的一塊區域，用于保存用戶進程的子程序間相互調用的參數、返回值、返回點以及子程序(函數)的局部變量。
   我們編寫的遞歸程序屬于用戶程序，因此使用的是用戶棧。

3. 棧溢出
   函數調用的參數是通過棧空間來傳遞的，在調用過程中會占用線程的棧資源。而遞歸調用，只有走到最后的結束點后函數才能依次退出，而未到達最后的結束點之前，占用的棧空間一直沒有釋放，如果遞歸調用次數過多，就可能導致占用的棧資源超過線程的最大值，從而導致棧溢出，導致程序的異常退出。

綜上:

函數調用的時候，每次調用時要做地址保存，參數傳遞等，這是通過一個遞歸工作棧實現的。具體是每次調用函數本身要保存的內容包括：局部變量、形參、調用函數地址、返回值。那么，如果遞歸調用N次，就要分配N次局部變量、N次形參、N次調用函數地址、N次返回值,勢必效率低.

優點

1. 代碼簡潔、清晰,易懂

循環能干的事,遞歸都能干;遞歸能干的循環不一定能干

對于我們,能用循環解決的,盡量不適用遞歸.