Factorizing Personalized Markov Chains for Next-Basket Recommendation
摘要和介紹
這篇文章發表于 WWW2010,當時主流的推薦方法是MF和MC
- MF(Matrix Factorization) : 用于建模用戶與物品的偏好。給定已知用戶和物品的交互,來預測矩陣中其他未知位置的用戶偏好,方法有SVD分解,隱變量模型和基于優化/學習的方法等。
- MC(Markov Chain): 用于建模用戶與商品交互的序列信息。MC方法基于轉移矩陣,通過上一時刻的交互來預測下一個時刻的用戶交互。
FPMC(Factorizing Personalized Markov Chains for Next-Basket Recommendation):
MF方法適合于建模personalized的推薦場景,MC方法適合于建模sequential的推薦場景,那么在Next-Basket Rec的任務中,如果既想考慮user-taste,又想考慮sequential信息,應該怎么做?
作者想了一個很自然的方法,那就是給每一個user建模一個markov transition matrix。也就是建模一個
任務介紹
首先為了說明MF和MC方法各有優缺點,Rendle舉了兩個例子:
- 有一個小伙平時愛看科幻電影,比如星戰之類的。有一天陪女朋友看了泰坦尼克號,MC模型傾向于下一個推薦浪漫電影,而MF是global recommender,MF傾向于推薦科幻片。這說明MC模型容易受到最近交互的噪聲影響。
- 有一個小伙買了camera,MF模型可能會繼續推薦電子產品,MC模型會推薦膠片之類的"配件"。這說明MF這種全局建模u-i關系的難以利用序列化信息,做next item的預測。
FPMC的任務:
已知用戶列表
方法
核心問題在于如何估算transition tensor的參數:
方法1: MLE 和 full parametrization
這是極大似然的估計方法,由于tensor的每一個位置都需要估算,所以又是一個全參數估計的方法。這種方法計算簡單,但是面臨一個問題, 就是每一個
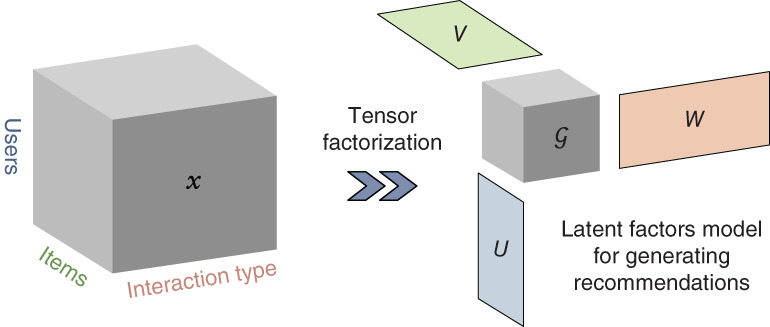
方法2:tensor分解
根據上面的分析,單獨考慮每一個user->item, 和 item->item之間的轉移概率估計,不能完全利用信息,這說明u-i和i-i之間的信息應該可以share。全參數的估計面臨稀疏性的問題,希望得到低秩表示。
Tucker分解:
顯然有如下的關系式:
考慮最簡單的單位tensor分解核:
通過上面的式子,可以看到這其實是向量內積做矩陣分解的tensor分解版本。
由于數據是稀疏的,Rendle 提出了下面的pairwise interaction的tensor分解:
對user,current item和next item 三者的pair關系設置兩方面的embedding,通過點積的和來估算:
這樣做的好處:
- 降低計算復雜度,相比較TD分解,這種分解方法參數量有所降低(因為沒有三維的core),分解和推斷的代價都會降低。
- 個人理解: 因為數據是稀疏的,TD分解想要降低復雜度,就只能使得core tensor更加稀疏,一個極端的情況,使用單位core tensor,這樣變成三個embedding的element-wise的乘法,如果數據(embedding)稀疏, 按位置乘法就有可能造成0位置過多。
- 顯式建模pairwise的interaction信息,可能更為直接。
回到MC:
這種建模方法比方法1的全參數建模參數量更少,而且解決了數據稀疏的問題。
訓練方法
對于序列中的每一個轉移,都可以采集作為偏序關系的學習樣本。
從t-1 -> t, 的轉移過程采用BPR優化器訓練,學習偏序關系。序列中的BPR優化方法被作者命名為S-BPR。
和MF/MC方法的關系
注意到在訓練的過程中,并沒有對current-item做負采樣,也就是說這個打分和括號里面和U,L相關的項,對于訓練過程都是一樣的,做差之后就抵消了,完全沒有影響。
所以在BPRloss下可以簡化為:
顯然前一項是描述U-I的關系的,可以視為MF項,后一項是描述I-I關系的,可以視為FMC項。
值得注意的是: 并不能將FPMC視為 簡單的MF,FMC線性相加。理由如下:
- 訓練是聯合的,不是單獨訓練拼起來
- 這是建立在優化器和采樣方法對U-L之間的關系沒有感知的基礎上
- 采用pairwise interaction的tensor分解方法才可能出現這種情況
所以應該將FMC+MF視為一種退化的解。
結果和啟示
- FMC和MC相比克服了數據稀疏的問題,而且這種低秩估計的分解方法不容易overfit。
- MF和FMC相比,在dense數據上MF更好,因為user相關的信息比較多。FMC在sparse數據上更好,因為這時沒有足夠的信息來學習用戶的偏好,反而是最后一項物品更重要。
- 無論在dense還是sparse,FPMC都比FMC和MF好。













logging)
和《機械制圖》 課程的結合、探索與實踐研究...)




