有一對兔子，從出生后的第3個月起每個月都生一對兔子。小兔子長到第3個月后每個月又生一對兔子，假設所有的兔子都不死，問30個月內每個月的兔子總數為多少？

問題分析

兔子數的規律，如下表所示：

月數

小兔子對數

中兔子對數

老兔子對數

兔子總數

1

1

0

0

1

2

0

1

0

1

3

1

0

1

2

4

1

1

1

3

5

2

1

2

5

6

3

2

3

8

7

5

3

5

13

提示：不滿1個月的兔子為小兔子，滿1個月不滿2個月的為中兔子，滿3個月以上的為老兔子。

可以看出，每個月的兔子總數依次為1, 1, 2, 3, 5, 8, 13…這就是Fibonacci數列。總結數列規律即從前兩個月的兔子數可以推出第3個月的兔子數。

算法設計

該題是典型的迭代循環，即是一個不斷用新值取代變量的舊值，然后由變量舊值遞推出變量新值的過程。這種迭代與如下因素有關：初值、迭代公式、迭代次數。經過問題分析，算法可以描述為：

用C語言來描述迭代公式即為：

fib = fib1 + fib2

其中 fib 為當前新求出的兔子數，fib1為前一個月的兔子數，fib2 中存放的是前兩個月的兔子數，然后為下一次迭代做準備，進行如下的賦值 fib2=fib1，fibl=fib，要注意賦值的次序，迭代次數由循環變量控制，表示所求的月數。

下面是完整的代碼：

#include

int main()

{

long fib1=1, fib2=1, fib;

int i;

printf("%12ld%12ld", fib1, fib2); /*輸出第一個月和第二個月的兔子數*/

for(i=3; i<=30; i++)

{

fib = fib1 + fib2; /*迭代求出當前月份的兔子數*/

printf("%12ld", fib); /*輸出當前月份兔子數*/

if(i % 4 == 0)

printf("n"); /*每行輸出4個*/

fib2 = fib1; /*為下一次迭代作準備，求出新的fib2*/

fib1 = fib; /*求出新的fib1*/

}

printf("n");

return 0;

}

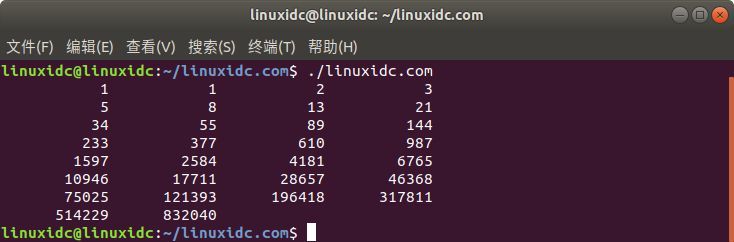
運行結果：

1 1 2 3

5 8 13 21

34 55 89 144

233 377 610 987

1597 2584 4181 6765

10946 17711 28657 46368

75025 121393 196418 317811

514229 832040

Linux公社的RSS地址：https://www.linuxidc.com/rssFeed.aspx

本文永久更新鏈接地址：https://www.linuxidc.com/Linux/2018-12/155896.htm