今天是機器學習專題的第27文章，我們一起來聊聊數據處理領域的降維(dimensionality reduction)算法。

我們都知道，圖片格式當中有一種叫做svg，這種格式的圖片無論我們將它放大多少倍，也不會失真更不會出現邊緣模糊的情況。原因也很簡單，因為這種圖片是矢量圖，一般的圖片存儲的是每一個像素點的顏色值，而在矢量圖當中，我們存儲的是矢量，也就是起點終點以及顏色。由于矢量圖只記錄起點終點，所以無論我們如何放大，圖片都不會失真，而傳統的圖片就做不到這一點。

其實svg就相當于圖片的降維，我們將上百萬的像素點簡化成了若干個矢量完成了圖片的存儲，大大減少了數據的規模。機器學習領域中的降維算法其實也是差不多的原理。

背景與原理

現在降維算法這個詞已經越來越少聽到了，在面試當中也很少被提及，這是有時代因素的。因為現在的計算資源以及存儲資源越來越廉價了，在以前很難承擔的計算量，現在變得越來越輕松。所以相對而言，降維算法沒有之前熱門了，也越來越少在面試當中出現。

從現狀倒推回從前，我們大概可以猜到，在若干年以前，當我們面臨海量無法承擔的數據的時候，降維算法是多么的重要。因為，我們都知道，機器學習訓練的速度和它使用的數據量有這非常密切的關系，使用10維特征和使用100維特征的模型的收斂速度至少是10倍以上的差距。那么，自然而然地我們就會想到，如果有某種方法可以將100維的數據”壓縮“成10維，該有多好？

但問題來了，數據不是實體，我們真的可以隨意壓縮嗎，這其中的原理是什么呢？

最根本的原理是既然特征可以用來訓練模型，那么特征的分布和label的分布必然是有一定的內在聯系的。也就是說數據并不是隨意分散的，而是彼此之間有聯系的。我們各種各樣的壓縮算法，本質上都是利用了數據之間的關聯。

舉個不是非常恰當，但是很直觀的例子。假設說我們現在有三個特征，分別是一個人的考試成績、智商以及努力程度。我們會很明顯地發現，考試成績和智商以及努力程度這兩個特征高度相關。如果我們能夠找到它們之間的關聯，我們完全可以去掉考試成績這個特征，而通過智商、努力程度和它的這種關聯來推算出這個值來。當然既然是推算出來的，顯然會和原本的值有一定的誤差，這也是不可避免的。

從這個例子當中，我們可以明確兩點，首先，壓縮數據是利用的數據分布的關聯或者是特性，如果是完全隨機的數據是無法降維壓縮的。其次，降維壓縮必然會帶來信息損失，也就是誤差，這是不可避免的。

降維算法

降維壓縮的算法有好幾種，常見的有PCA、ICA和FA，下面我們來簡單介紹一下。

首先是PCA，PCA的英文全稱是Principal Component Analysis即主成分分析。這種方法的主要原理是對數據進行坐標變換，即將數據從原來的坐標系更換到新的坐標系。新的坐標軸是通過最大方差理論推導得到的，即新的坐標軸包含了原始數據中大部分的方差，這里的方差可以理解成信息。

ICA的英文是Independent Component Analysis即獨立成分分析，在這個算法當中它假設數據是通過N個數據源生成的。假設數據是這N個數據源數據混合觀察的結果。這些數據源在統計上是互相獨立的，如果數據源的數目少于原始特征的數目，也可以完成降維。

最后是FA即Factor Analysis即因子分析。在因子分析當中，我們假設樣本當中存在一些隱變量，我們假設樣本是這些隱變量和一些噪音的線性組合。那么只要這些隱變量的數量少于原始特征的數量，我們就可以用這些隱變量來作為新的數據從而實現降維。

這三種降維算法雖然各不相同，但是核心的思路都是一致的。都是假設數據的分布滿足某一種特性，通過利用這一種特性來對數據進行壓縮。這其中使用范圍最廣的是PCA，所以我們著重來了解一下PCA的原理以及實現。

理論推導

關于PCA算法有兩種通俗的解釋，一種是最大方差理論，另外一種是最小化降維損失，這兩個思路推導出的結果是一樣的。相比之下，最大方差理論更加容易理解一些，所以我們就選擇最大方差理論來做個簡單的解釋。

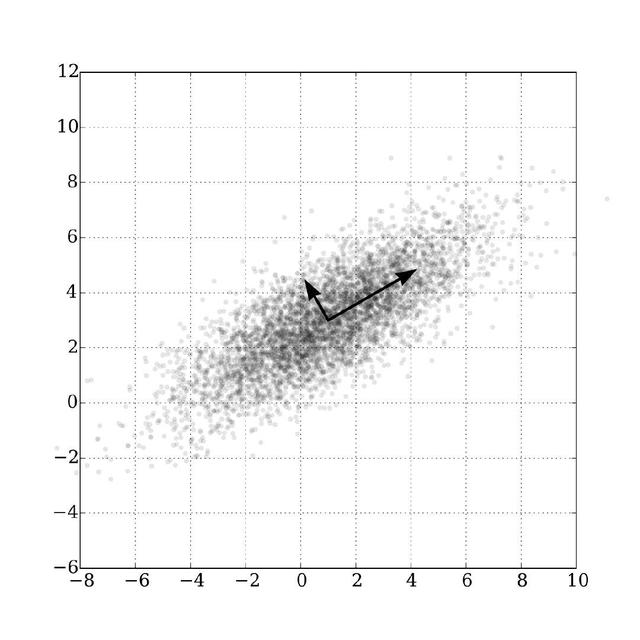
在信號系統當中，我們普遍認為信號具有較大的方差，而噪音擁有較小的方差。信噪比就是信號與噪聲的方差比，這個比值越大越好，越大說明噪音越小，信號的質量越高。比如下圖當中的這個數據分布，我們可以在原始數據當中找到兩個正交軸，根據方差最大理論，我們會把方差大的那個軸看成是信號，方差小的看成是噪音。

根據這個思路，最好的k維特征是將n維的樣本轉換成k維坐標之后，擁有最大方差的k個。

協方差

到這里，我們雖然知道了要獲取方差最大的方向作為新的坐標軸，但是如果我們直接去計算的話是會有問題的。最大的問題在于我們沒辦法選出K個來，如果只是選擇類似的K個方向，這K個軸的信息都差不多，會丟失大量的信息。所以我們不僅要選擇K個軸，而且要保證這K個軸盡可能線性無關。

要做到線性無關，也就是說這K個軸應該是彼此正交的。如果兩個軸正交，可以進一步得到這兩個軸的協方差為零。為了簡化運算，我們可以先讓原始數據全部減去各自特征的均值。在去除均值之后，兩個特征的協方差可以表示為：

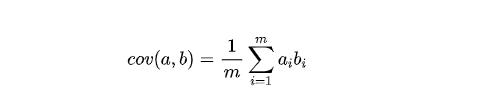
兩個特征正交等價于它們的協方差為0，我們假設去除了均值之后的矩陣為X，我們來寫出它的協方差矩陣。

協方差矩陣

對于去除了均值的矩陣X而言，有一個性質是它的協方差矩陣

X_cov=1/m X X^T。我們可以來簡單證明一下，假設矩陣當中只有兩個特征a和b，那么我們將它按行寫成矩陣：

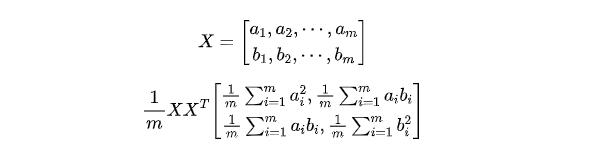
我們假設X的協方差矩陣為C，那么C是一個對稱矩陣，它的對角線上的元素表示各個特征的方差，其他的元素則表示特征之間的協方差。我們的目標是希望能夠得到一個類似形式的對角矩陣，也就是說除了對角線之外的其余元素全為0，這樣這些特征之間就是正交矩陣，我們根據對角線上的值挑選出方差最大的K個特征即可。

我們的目的和方向已經很明確了，距離終點只有一步之遙，但是這一步怎么邁過去呢？

對角化

這里我們采用逆向思維來思考，假設我們已經找到了矩陣P，通過P對X進行線性變換的結果是Y，那么Y=PX，我們假設Y的協方差矩陣為D，那么根據剛才我們推導的結論可以得到：

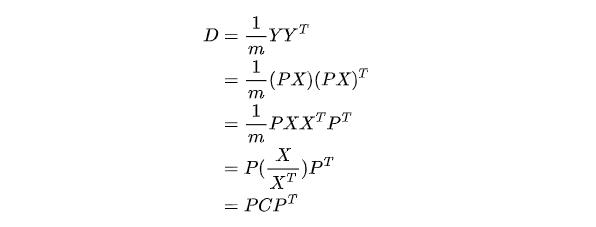
我們希望D是一個對角矩陣，所以我們要尋找的就是P，P找到之后一切都迎刃而解。因為D是一個對角矩陣，我們將它對角的元素從大到小排列之后，對應P的行組成的矩陣就是我們尋找的基。我們用P的前K行組成的新矩陣對原始數據X進行線性變換，就將它從n維降低到了K維。

所以問題就只剩下了一個，這個P矩陣要怎么求呢？我們干想是很困難的，其實數據家們已經給了我們答案，就是C矩陣的特征向量。

由于C是對稱矩陣，根據線性代數的原理，它有如下兩條性質：

1. 對稱矩陣不同的特征值對應的特征向量必然正交
2. 特征值是實數，K重特征值對應的線性無關的特征向量剛好有K個

根據這兩條性質，我們可以得到，對于n*n的矩陣C來說，我們可以找到n個特征向量 e_1, e_2, ... , e_n。我們將它們按列組成矩陣：

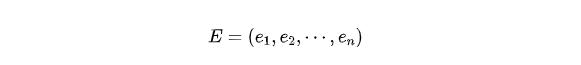
我們通過E可以將C對角化：

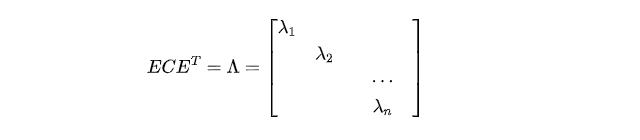
我們對Lambda中的特征值從大到小排列，選出前K個特征值對應的特征向量組成矩陣即得到了最終的結果P。

最后，我們整理一下上述的整個過程。

1. 每一維特征減去平均值
2. 計算協方差矩陣
3. 求解協方差矩陣的特征值和特征向量
4. 對特征值降序排序，選擇其中最大的K個，然后將對應的K個特征向量作為行向量組成特征向量P
5. 轉換之后的結果X_t = PX

我們把這個邏輯整理一下，寫成代碼：

import numpy as npdef pca(df, k):    mean = np.mean(df, axis=0)    new_df = df - mean    # 計算協方差矩陣，也可以用公式自己算    cov = np.cov(new_df, rowvar=0)    # 求解矩陣特征值和特征向量    eigVals, eigVects = np.linalg.eig(np.mat(cov))    # 對特征值排序，選最大的K個，由于是從小到大排，所以我們取反    eigValIndice = np.argsort(-eigVals)    # 構建變換矩陣    n_eigValIndice = eigValIndice[:k]    n_eigVect = eigVects[:, n_eigValIndice]    data_ret = new_df.dot(n_eigVect)    return data_ret

實戰驗證

為了驗證程序效果，我們找了一份經典的機器學習數據：http://archive.ics.uci.edu/ml/datasets/SECOM。

我們把它下載下來之后，用pandas讀入進來：

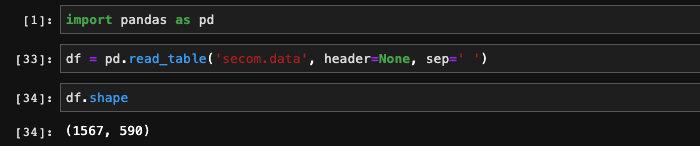
可以看到它的特征有590維，展開看的話會發現特征當中有許多空值：

我們對它進行一個簡單地預處理，將空值替換成特征均值，并且再讀入label的值：

為了驗證PCA降維的效果，我們用同樣一份數據，用同樣的模型，比較一下做PCA之前和之后模型的效果。

這里我選擇的是隨機森林，其實不管用什么模型都大同小異。我們將數據拆分成訓練數據與測試數據，并且調用skelarn庫當中的隨機森林完成訓練和預測，最后計算模型在測試集當中的表現。說起來挺復雜，但是由于sklearn替我們完成了大量的工作，所以用到的代碼并不多：

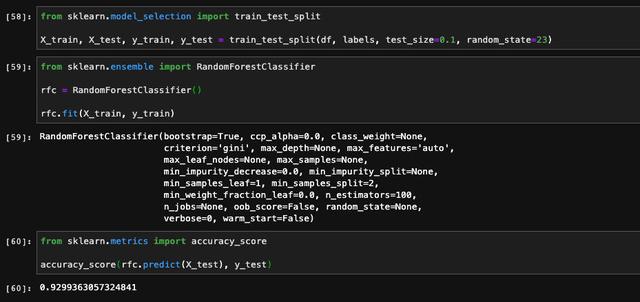
我們可以看到，在PCA之前，隨機森林在測試集上的表現是92.3%的準確率。

接下來，我們用同樣的數據和模型來驗證PCA之后對于模型性能的影響。為了保證數據集的完全一致，我們把測試集的隨機種子也設置成一樣。

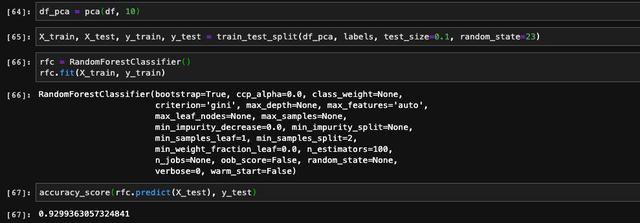
可以看到模型在測試集上的準確率完全一樣，說明PCA并沒有過多降低模型的性能，和我們的預期一致。

總結

在今天的文章當中，我們詳細介紹并推導了PCA背后的原理，并采取實際數據集驗證了PCA算法的效果。從最后的結果上來看，雖然我們將590維的特征縮減到了10維，但是模型的效果卻幾乎沒有多大影響，可見PCA的威力。

當然，這背后的因素很多，除了PCA本身的原理之外，和數據的分布以及訓練測試樣本的數量也有關系。在極端場景下，可能特征的數量非常多，含有大量的噪音，如果我們不做降維直接訓練的話，很有可能導致模型很難收斂。在這種情況下，使用降維算法是必要的，而且會帶來正向的提升。如果特征數量不多，模型能夠收斂，使用降維算法可能沒什么助益，而且會稍稍降低模型的效果。但在一般的情況下，數據集特征的分布也符合二八定律，即20%的特征帶來80%以上的貢獻，大部分特征效果不明顯，或者噪音很多。在這種情況下，使用PCA進行降維，幾乎是一定起到正向作用的。

當然在實際的應用場景當中，降維算法用的越來越少，除了計算能力提升之外，另外一個很重要的原因是深度學習的興起。深度神經網絡本身就帶有特征篩選的效果，它自己會選擇合適的特征組合達到最好的效果，所以很多特征處理和降維等操作顯得不是特別有必要了。雖然如此，但是算法本身的思想還是很有借鑒作用，PCA算法在Kaggle比賽當中使用頻率也很高，對它進行詳細地了解和學習還是很有必要的。

今天的文章就到這里，如果喜歡本文，可以的話，請點個贊和關注吧，給我一點鼓勵，也方便獲取更多文章。

本文始發于公眾號：TechFlow