

NumPy包是python生態系統中數據分析、機器學習和科學計算的主力。 它極大地簡化了向量和矩陣的操作。Python的一些主要軟件包依賴于NumPy作為其基礎架構的基礎部分(例如scikit-learn、SciPy、pandas和tensorflow)。我們將介紹一些使用NumPy的主要方法,以及在我們為機器學習模型提供服務之前它如何表示不同類型的數據(表格、聲音和圖像)。
import numpy as np
一、數組操作
1.1創建數組
通過將python列表傳遞給NumPy對象,使用np.array()創建一個NumPy數組(即ndarray)。 Python創建了我們在右邊可以看到的數組:
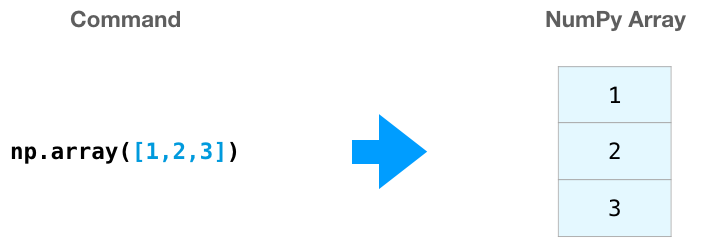
一般情況,我們希望直接使用NumPy作為初始化的數組數據。 NumPy為這些情況提供了諸如ones(),zeros()和random.random()類等方法。 我們只需要向這些方法傳遞要生成的元素數量的參數:
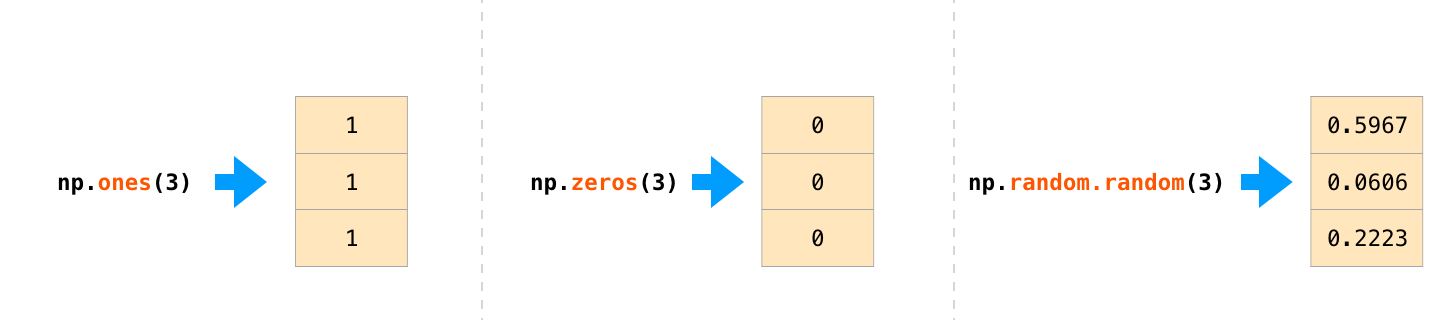
一旦我們創建了數組,我們就可以開始以有趣的方式操作它們。
1.2 數組算術
先來創建兩個NumPy數組來展示它們的用處。 我們稱之為data和ones:

這兩個數組的加法就像我們+1那么簡單(每一行相加)。
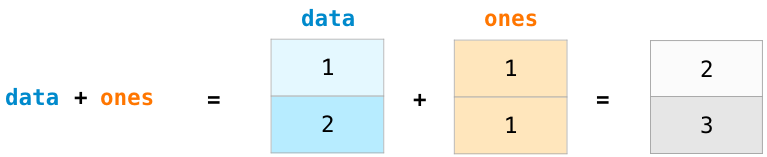
可以發現這樣的計算不必在循環中實現。 這是非常好的抽象處理,可以讓你在更高層次上思考問題,而不是陷入如何實現計算的算法里面。
我們還可以像下面一樣進行其他運算:

通常情況下,我們希望在數組和單個數字之間執行操作(我們也可以將其稱為向量和標量之間的操作)。 比如說,我們的數組表示以英里為單位的距離,我們希望將其轉換為公里數。 我們只需要讓數據* 1.6就可以了。

NumPy讓每個單元格都會發生相乘叫做廣播。
1.3索引數組
我們可以索引、切片NumPy數組。

1.4 數組聚合
NumPy為我們提供非常好用的聚合功能:

除了最小值、最大值和總和之外,還得到非常棒的東西,比如平均值、所有元素相乘的結果、標準差,以及其他很多。
二、多維處理
2.1 創建矩陣
所有的例子都在一個維度上處理向量。 NumPy的厲害之處是能夠將我們目前所看到的所有內容應用到任意維度上。我們可以傳遞一個Python列表,讓NumPy創建一個矩陣來表示它們:
np.array([[1,2],[3,4]])

我們也可以使用上面提到的相同方法(ones(),zeros()和random.random()),只要我們給它們一個元組來描述我們正在創建的矩陣的維度:

2.2 矩陣算術
如果兩個矩陣的大小相同,我們可以使用算術運算符(+ – * /)來進行矩陣計算。NumPy將這些作為位置操作處理:
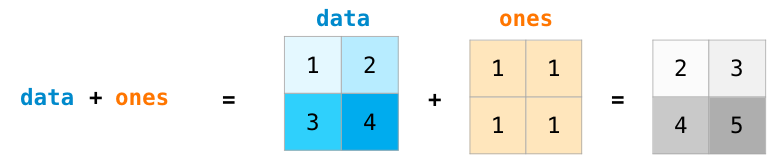
只有當不同維度為1時(例如矩陣只有一列或一行),我們才能在不同大小的矩陣上進行這些算術運算,在這種情況下,NumPy將其廣播規則用于該操作:

2.3 點積
NumPy為每個矩陣提供了一個dot()方法,我們可以用它來執行與其他矩陣的點積運算:

兩個矩陣在它們彼此面對的一側必須具有相同的尺寸(上圖底部紅色的數字)。
您可以將此操作可視化為如下所示:

2.4 矩陣索引
當我們操作矩陣時,索引和切片操作變得更加有用:
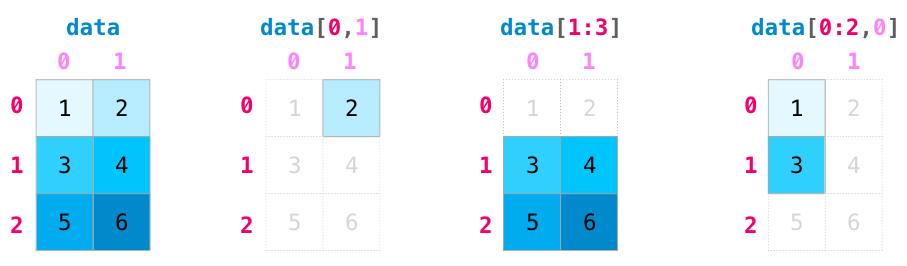
冒號表示從哪個位置到哪個位置,留空表示開頭或者結尾;逗號表示行和列。NumPy的索引是從0開始的,并且后面的方括號是不包含后面的值(即小于后面的值)。
2.5 矩陣聚合
我們可以像聚合向量一樣聚合矩陣:

我們不僅可以聚合矩陣中的所有值,還可以使用axis參數在行或列之間進行聚合:

2.6 轉置和重塑
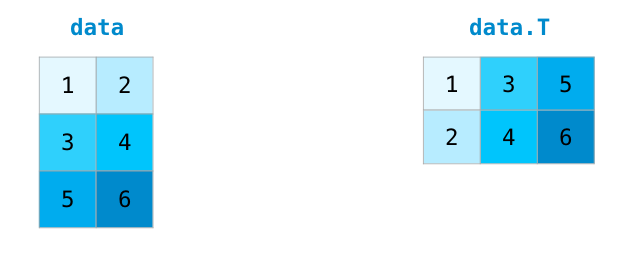
處理矩陣時的一個共同需求是需要旋轉矩陣。 當我們需要采用兩個矩陣的點積并需要對齊它們共享的維度時,通常就是這種情況。 NumPy數組有一個方便的屬性叫做T來獲得矩陣的轉置:
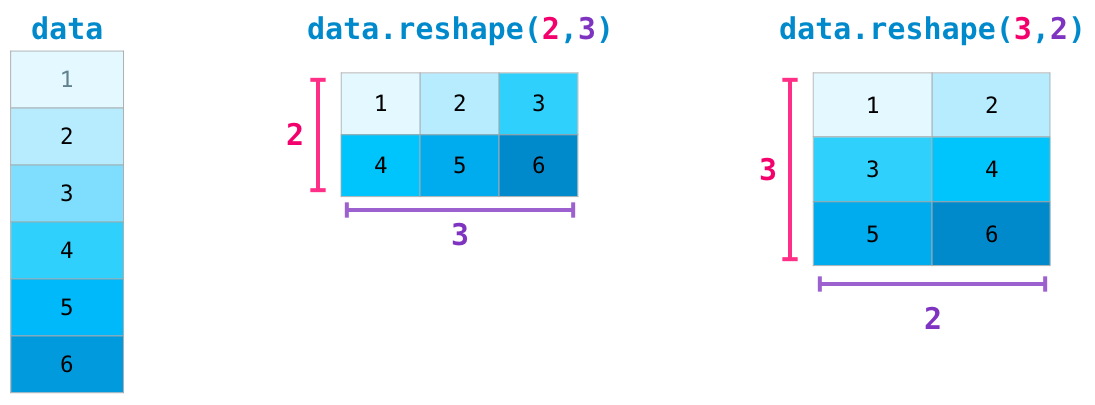
在更高級的應用中,您可能會發現自己需要切換某個矩陣的維度。 在機器學習應用程序中通常就是這種情況,其中某個模型期望輸入的某個形狀與您的數據集不同。 在這些情況下,NumPy的reshape()法很有用。 您只需將矩陣所需的新尺寸傳遞給它即可。
2.7 更多維度
NumPy可以完成我們在任何維度定義數據。 其中心數據結構稱為ndarray(N維數組)。

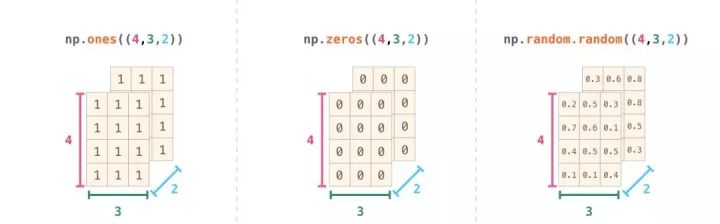
在很多方面,處理新維度只需在NumPy函數的參數中添加逗號:
三、公式計算
我們舉一個計算均方誤差的例子。實現適用于矩陣和向量的數學公式是考慮NumPy的關鍵用例。例如均方誤差MSE公式,它是監督機器學習、模型處理、回歸問題的核心公式:
在NumPy中實現這一點是輕而易舉的:

這樣做的好處是我們不需要關心predictions和labels是否包含一個或一百個值(只要它們的大小相同)。我們可以通過一個示例逐步執行該代碼行中的四個操作:

predictions和labels向量都包含三個值。 這意味著n的值為3。 在我們執行減法后,我們最終得到如下值:

然后我們可以對矢量中的值進行平方:

然后求和:

結果就是均方誤差。
四、數據表示
4.1 表格和電子表格
構建模型所需的所有數據類型(電子表格、圖像和音頻等),很多都非常適合在n維數組中表示。
電子表格或值表是二維矩陣。 電子表格中的每個工作表都可以是自己的變量。 Python中最受歡迎的抽象是pandas數據幀DataFrame,它實際上使用NumPy并在其上構建。
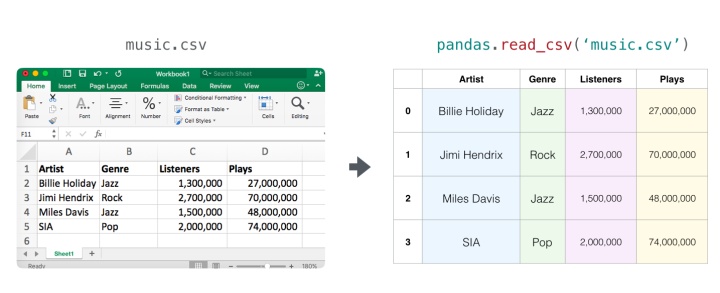
4.2 音頻
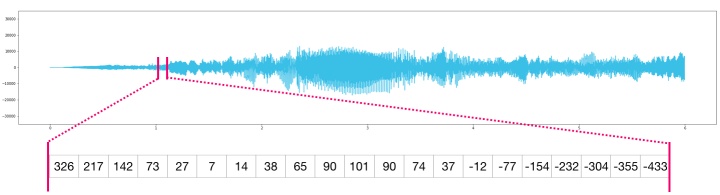
音頻文件是一維樣本數組。 每個樣本都是一個代表音頻信號的一小部分的數字。 CD質量的音頻每秒可能有44,100個樣本,每個樣本是-65535到65536之間的整數。這意味著如果你有一個10秒的CD質量的WAVE文件,你可以將它加載到長度為10 * 44,100的NumPy數組中 = 441,000個樣本。 想要提取音頻的第一秒? 只需將文件加載到我們稱之為audio的NumPy數組中,然后獲取audio[:44100]。
以下是一段音頻文件:
4.3 圖像
圖像是高度×寬度的像素矩陣。如果圖像是黑白的(即灰度),則每個像素可以由單個數字表示(通常在0(黑色)和255(白色)之間)。
想要裁剪圖像的左上角10 x 10像素部分? 告訴NumPy讓你image[:10,:10]。
這是一個圖像文件的片段:
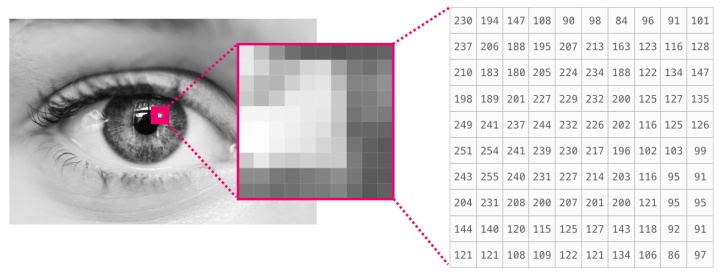
如果圖像是彩色的,則每個像素由三個數字表示(RGB)。 在這種情況下,我們需要第三維(因為每個單元格只能包含一個數字)。 因此彩色圖像由尺寸的ndarray表示:(高x寬x 3)。






)







)





