混淆矩陣的精度計算公式為：精度=(TP+TN)/(TP+TN+FP+FN)，也就是說，精度就是指正確的預測數目除以所有樣本的數量。

準確率、召回率與f-分數：總結混淆矩陣還有幾種方法，其中最常見的就是準確率和召回率。準確率度量的是被預測為正例的樣本有多少是整整的樣例。即：準確率=TP/(TP+FP)。如果目標是限制假正例的數量，那么可以使用準確率作為性能目標。

召回率：召回率(recalll)度量的是正類樣本中有多少被預測為正類，即：召回率=TP/(TP+FN)，如果我們需要找出所有的正類樣本，即避免反例是很重要的情況下，那么可以使用召回率作為性能指標。

在優化召回率與優化準確率之間需要折中，如果你預測所有樣本都屬于正類，那么可以輕松得到完美的召回率(沒有假反例、也沒有真反例)。但是，將所有樣本都預測為正類，將會得得很多假正例，因此準確率會很低。與之相反，如果你的模型只講一個最確定的數據點預測為正類，其他點都預測為反類，那么準確率將會很完美(假設這個數據點上實際上就屬于正類)，但是召回率會很差。(當然，準確率和召回率只是度量混淆矩陣情況中兩個量，其他的可以根據實際情況取對應的參數)。

f-分數：雖然準確率和召回率是非常重要的度量，三式僅查看二者之一無法提供完美的途徑，所以還有一種將兩種方法匯總的方法——f-分數。它是準確率與召回率的調和平均，即：F=2*(準確率*召回率)/(準確率+召回率)。

由于f-分數同時考慮了準確率和召回率，所以它對于不平衡的二分類數據集來說是一種比精度更好的度量方式。我們對前面提到過的“9與其余”的數據集的預測結果計算f1-分數(我們這里假設“9”是正類，標記為True，其他樣本為False)：

from sklearn.metrics import f1_score

print("F1 score most frequent: {:.2f}".format(f1_score(y_test, pred_most_frequent)))

print("F1 score dummy: {:.2f}".format(f1_score(y_test, pred_dummy)))

print("F1 score logreg: {:.2f}".format(f1_score(y_test, pred_logreg)))

print("F1 score of Tree: {:.2f}".format(f1_score(y_test, pred_tree)))

運行后其結果如下：

F1 score most frequent: 0.00

F1 score dummy: 0.13

F1 score logreg: 0.89

F1 score of Tree: 0.55

由運行結果可以看出：most_frequency的預測中得到的是一條錯誤信息；另外需要注意的是，虛擬預測和決策樹預測之間還是有差別的，盡管精度差別不大，但是f-分數卻相差很大。在這里，f-分數更加符合我們對模型的直覺。f-分數的缺點則是比精度更加難以解釋。

如果我們要對準確率、召回率和f1-分數做一個更加全面的總結，則可以使用classification_report這個函數，它可以同時計算這三個值，并以美觀的形式打印出來。

from sklearn.metrics import classification_report

print("Most frequency class precious:")

print(classification_report(y_test, pred_most_frequent, target_names=["not Nine", "Nine"]))

print("Dummy model precious:")

print(classification_report(y_test, pred_dummy, target_names=["not Nine", "Nine"]))

print("Decision tree precious:")

print(classification_report(y_test, pred_tree, target_names=["not Nine", "Nine"]))

print("logistic regression precious")

print(classification_report(y_test, pred_logreg, target_names=["not Nine", "Nine"]))

運行結果如下圖：

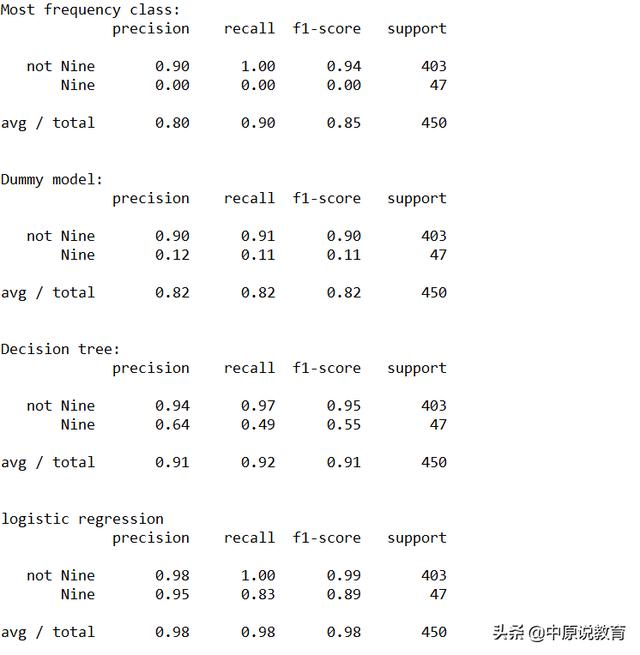
classification_report函數為每個類別(這里是True和False)生成一行，并給出以該類并為正類的準確率、召回率及f-分數。這里的最后一列support(支持)表示的是在這個類別中真實樣本的數量；最后一行顯示的是對應指標的加權平均(按每個類別中的樣本個數加權)。

同時，我們從運行結果中還可以看出，虛擬模型與logreg之間的區別并不是很明顯，選擇哪個類作為正類對指標有很大影響。在這里選擇Nine作為正類時logisticregression比其他方法更具備優勢。