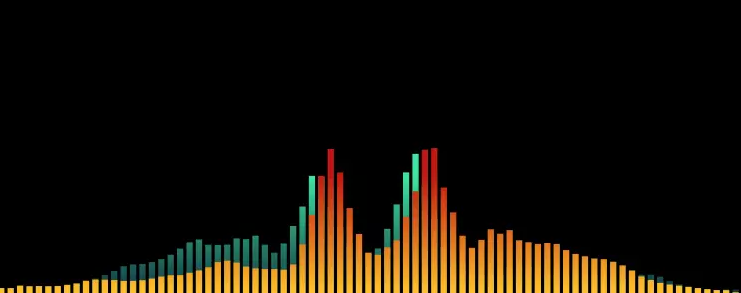
本文是系列文章中的第二篇，上篇講述了音頻播放和頻譜數據計算，本篇講述數據處理和動畫的繪制。

前言

在上篇文章中我們已經拿到了頻譜數據，也知道了數組每個元素表示的是振幅，那這些數組元素之間有什么關系呢？根據FFT的原理， N個音頻信號樣本參與計算將產生N/2個數據(2048/2=1024)，其頻率分辨率△f=Fs/N = 44100/2048≈21.5hz，而相鄰數據的頻率間隔是一樣的，因此這1024個數據分別代表頻率在0hz、21.5hz、43.0hz....22050hz下的振幅。

那是不是可以直接將這1024個數據繪制成動畫？當然可以，如果你剛好要顯示1024個動畫物件！但是如果你想可以靈活地調整這個數量，那么需要進行頻帶劃分。嚴格來說，結果有1025個，因為在上篇文章的FFT計算中通過fftInOut.imagp[0] = 0，直接把第1025個值舍棄掉了。這第1025個值代表的是奈奎斯特頻率值的實部。至于為什么保存在第一個FFT結果的虛部中，請翻看第一篇。

頻帶劃分

頻帶劃分更重要的原因其實是這樣的：根據心理聲學，人耳能容易的分辨出100hz和200hz的音調不同，但是很難分辨出8100hz和8200hz的音調不同，盡管它們各自都是相差100hz，可以說頻率和音調之間的變化并不是呈線性關系，而是某種對數的關系。因此在實現動畫時將數據從等頻率間隔劃分成對數增長的間隔更合乎人類的聽感。

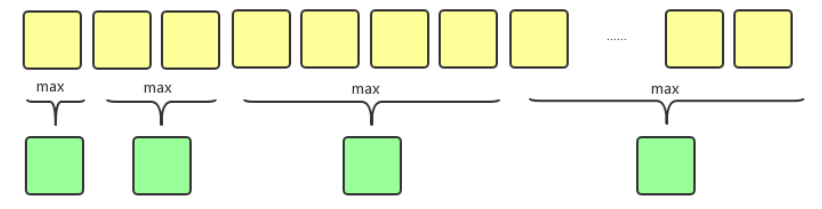
圖1 頻帶劃分方式

打開項目AudioSpectrum02-starter，您會發現跟之前的AudioSpectrum01項目有些許不同，它將FFT相關的計算移到了新增的類RealtimeAnalyzer中，使得AudioSpectrumPlayer和RealtimeAnalyzer兩個類的職責更為明確。如果你只是想瀏覽實現代碼，打開項目AudioSpectrum02-final即可，已經完成本篇文章的所有代碼

查看RealtimeAnalyzer類的代碼，其中已經定義了 frequencyBands、startFrequency、endFrequency 三個屬性，它們將決定頻帶的數量和起止頻率范圍。

public?var?frequencyBands:?Int?=?80?//頻帶數量

public?var?startFrequency:?Float?=?100?//起始頻率

public?var?endFrequency:?Float?=?18000?//截止頻率

現在可以根據這幾個屬性確定新的頻帶:private?lazy?var?bands:?[(lowerFrequency:?Float,?upperFrequency:?Float)]?=?{

var?bands?=?[(lowerFrequency:?Float,?upperFrequency:?Float)]()

//1：根據起止頻譜、頻帶數量確定增長的倍數：2^n

let?n?=?log2(endFrequency/startFrequency)?/?Float(frequencyBands)

var?nextBand:?(lowerFrequency:?Float,?upperFrequency:?Float)?=?(startFrequency,?0)

for?i?in?1...frequencyBands?{

//2：頻帶的上頻點是下頻點的2^n倍

let?highFrequency?=?nextBand.lowerFrequency?*?powf(2,?n)

nextBand.upperFrequency?=?i?==?frequencyBands???endFrequency?:?highFrequency

bands.append(nextBand)

nextBand.lowerFrequency?=?highFrequency

}

return?bands

}()

接著創建函數findMaxAmplitude用來計算新頻帶的值，采用的方法是找出落在該頻帶范圍內的原始振幅數據的最大值：private?func?findMaxAmplitude(for?band:(lowerFrequency:?Float,?upperFrequency:?Float),?in?amplitudes:?[Float],?with?bandWidth:?Float)?->?Float?{

let?startIndex?=?Int(round(band.lowerFrequency?/?bandWidth))

let?endIndex?=?min(Int(round(band.upperFrequency?/?bandWidth)),?amplitudes.count?-?1)

return?amplitudes[startIndex...endIndex].max()!

}

這樣就可以通過新的analyse函數接收音頻原始數據并向外提供加工好的頻譜數據：func?analyse(with?buffer:?AVAudioPCMBuffer)?->?[[Float]]?{

let?channelsAmplitudes?=?fft(buffer)

var?spectra?=?[[Float]]()

for?amplitudes?in?channelsAmplitudes?{

let?spectrum?=?bands.map?{

findMaxAmplitude(for:?$0,?in:?amplitudes,?with:?Float(buffer.format.sampleRate)??/?Float(self.fftSize))

}

spectra.append(spectrum)

}

return?spectra

}

動畫繪制

看上去數據都處理好了，讓我們捋一捋袖子開始繪制動畫了！打開自定義視圖SpectrumView文件，首先創建兩個CAGradientLayer：var?leftGradientLayer?=?CAGradientLayer()

var?rightGradientLayer?=?CAGradientLayer()

新建函數setupView()，分別設置它們的colors和locations屬性，這兩個屬性分別決定漸變層的顏色和位置，再將它們添加到視圖的layer層中，它們將承載左右兩個聲道的動畫。private?func?setupView()?{

rightGradientLayer.colors?=?[UIColor.init(red:?52/255,?green:?232/255,?blue:?158/255,?alpha:?1.0).cgColor,

UIColor.init(red:?15/255,?green:?52/255,?blue:?67/255,?alpha:?1.0).cgColor]

rightGradientLayer.locations?=?[0.6,?1.0]

self.layer.addSublayer(rightGradientLayer)

leftGradientLayer.colors?=?[UIColor.init(red:?194/255,?green:?21/255,?blue:?0/255,?alpha:?1.0).cgColor,

UIColor.init(red:?255/255,?green:?197/255,?blue:?0/255,?alpha:?1.0).cgColor]

leftGradientLayer.locations?=?[0.6,?1.0]

self.layer.addSublayer(leftGradientLayer)

}

接著在View的初始化函數init(frame: CGRect) 和 init?(coder aDecoder: NSCoder)中調用它，以便在代碼或者Storyboard中創建SpectrumView時都可以正確地進行初始化。override?init(frame:?CGRect)?{

super.init(frame:?frame)

setupView()

}

required?init?(coder?aDecoder:?NSCoder)?{

super.init(coder:?aDecoder)

setupView()

}

關鍵的來了，定義一個spectra屬性對外接收頻譜數據，并通過屬性觀察didSet創建兩個聲道的柱狀圖的UIBezierPath，經過CAShapeLayer包裝后應用到各自CAGradientLayer的mask屬性中，就得到了漸變的柱狀圖效果。var?spectra:[[Float]]??{

didSet?{

if?let?spectra?=?spectra?{

//?left?channel

let?leftPath?=?UIBezierPath()

for?(i,?amplitude)?in?spectra[0].enumerated()?{

let?x?=?CGFloat(i)?*?(barWidth?+?space)?+?space

let?y?=?translateAmplitudeToYPosition(amplitude:?amplitude)

let?bar?=?UIBezierPath(rect:?CGRect(x:?x,?y:?y,?width:?barWidth,?height:?bounds.height?-?bottomSpace?-?y))

leftPath.append(bar)

}

let?leftMaskLayer?=?CAShapeLayer()

leftMaskLayer.path?=?leftPath.cgPath

leftGradientLayer.frame?=?CGRect(x:?0,?y:?topSpace,?width:?bounds.width,?height:?bounds.height?-?topSpace?-?bottomSpace)

leftGradientLayer.mask?=?leftMaskLayer

//?right?channel

if?spectra.count?>=?2?{

let?rightPath?=?UIBezierPath()

for?(i,?amplitude)?in?spectra[1].enumerated()?{

let?x?=?CGFloat(spectra[1].count?-?1?-?i)?*?(barWidth?+?space)?+?space

let?y?=?translateAmplitudeToYPosition(amplitude:?amplitude)

let?bar?=?UIBezierPath(rect:?CGRect(x:?x,?y:?y,?width:?barWidth,?height:?bounds.height?-?bottomSpace?-?y))

rightPath.append(bar)

}

let?rightMaskLayer?=?CAShapeLayer()

rightMaskLayer.path?=?rightPath.cgPath

rightGradientLayer.frame?=?CGRect(x:?0,?y:?topSpace,?width:?bounds.width,?height:?bounds.height?-?topSpace?-?bottomSpace)

rightGradientLayer.mask?=?rightMaskLayer

}

}

}

}

其中translateAmplitudeToYPosition函數的作用是將振幅轉換成視圖坐標系中的Y值：private?func?translateAmplitudeToYPosition(amplitude:?Float)?->?CGFloat{

let?barHeight:?CGFloat?=?CGFloat(amplitude)?*?(bounds.height?-?bottomSpace?-?topSpace)

return?bounds.height?-?bottomSpace?-?barHeight

}

回到ViewController，在SpectrumPlayerDelegate的方法中直接將接收到的數據交給spectrumView://?MARK:?SpectrumPlayerDelegate

extension?ViewController:?AudioSpectrumPlayerDelegate?{

func?player(_?player:?AudioSpectrumPlayer,?didGenerateSpectrum?spectra:?[[Float]])?{

DispatchQueue.main.async?{

//1:?將數據交給spectrumView

self.spectrumView.spectra?=?spectra

}

}

}

敲了這么多代碼，終于可以運行一下看看效果了！額...看上去效果好像不太妙啊。請放心，喝杯咖啡放松一下，待會一個一個來解決。

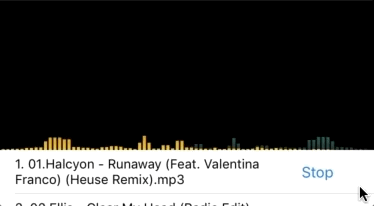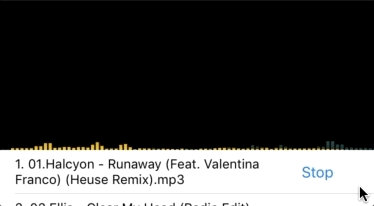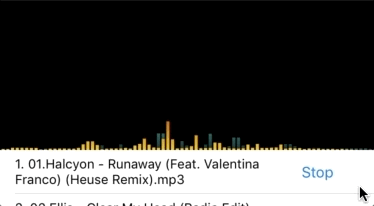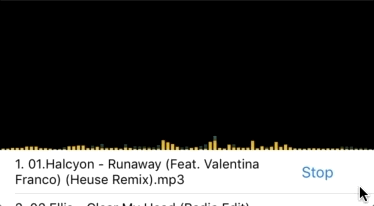
圖2 初始動畫效果

調整優化

效果不好主要體現在這三點：1)動畫與音樂節奏匹配度不高；2)畫面鋸齒過多； 3)動畫閃動明顯。 首先來解決第一個問題:

節奏匹配

匹配度不高的一部分原因是目前的動畫幅度太小了，特別是中高頻部分。我們先放大個5倍看看效果，修改analyse函數：func?analyse(with?buffer:?AVAudioPCMBuffer)?->?[[Float]]?{

let?channelsAmplitudes?=?fft(buffer)

var?spectra?=?[[Float]]()

for?amplitudes?in?channelsAmplitudes?{

let?spectrum?=?bands.map?{

//1:?直接在此函數調用后乘以5

findMaxAmplitude(for:?$0,?in:?amplitudes,?with:?Float(buffer.format.sampleRate)??/?Float(self.fftSize))?*?5

}

spectra.append(spectrum)

}

return?spectra

}

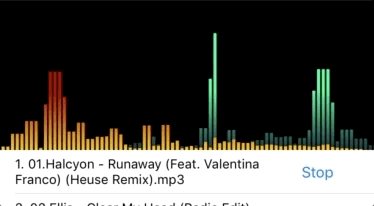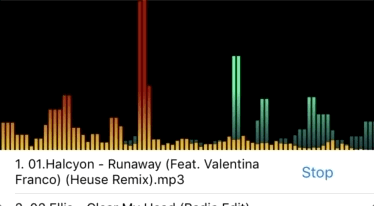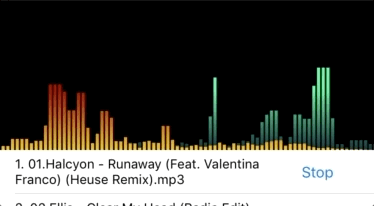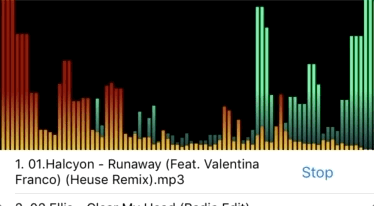
圖3 幅度放大5倍之后，低頻部分都超出畫面了

低頻部分的能量相比中高頻大許多，但實際上低音聽上去并沒有那么明顯，這是為什么呢？這里涉及到響度的概念：響度(loudness又稱音響或音量)，是與聲強相對應的聲音大小的知覺量。聲強是客觀的物理量，響度是主觀的心理量。響度不僅跟聲強有關，還跟頻率有關。不同頻率的純音，在和1000Hz某個聲壓級純音等響時，其聲壓級也不相同。這樣的不同聲壓級，作為頻率函數所形成的曲線，稱為等響度曲線。改變這個1000Hz純音的聲壓級，可以得到一組等響度曲線。最下方的0方曲線表示人類能聽到的最小的聲音響度，即聽閾；最上方是人類能承受的最大的聲音響度，即痛閾。

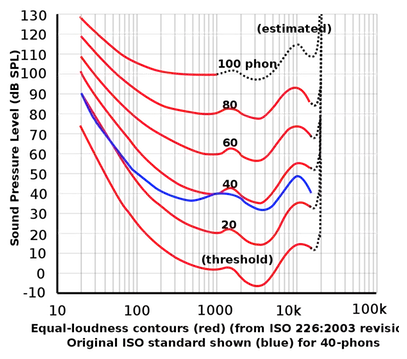
圖4 橫坐標為頻率，縱坐標為聲壓級，波動的一條條曲線就是等響度曲線(equal-loudness contours)，這些曲線代表著聲音的頻率和聲壓級在相同響度級中的關聯。

原來人耳對不同頻率的聲音敏感度不同，兩個聲音即使聲壓級相同，如果頻率不同那感受到的響度也不同。基于這個原因，需要采用某種頻率計權來模擬使得像人耳聽上去的那樣。常用的計權方式有A、B、C、D等，A計權最為常用，對低頻部分相比其他計權有著最多的衰減，這里也將采用A計權。

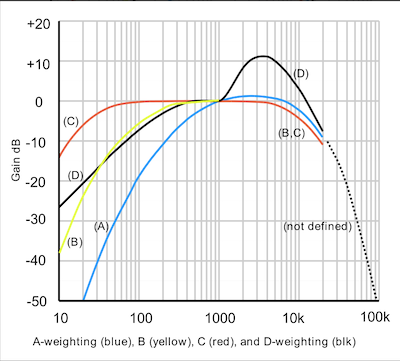
圖5 藍色曲線就是A計權，是根據40 phon的等響曲線模擬出來的反曲線

在RealtimeAnalyzer類中新建函數createFrequencyWeights()，它將返回A計權的系數數組：

private?func?createFrequencyWeights()?->?[Float]?{

let?Δf?=?44100.0?/?Float(fftSize)

let?bins?=?fftSize?/?2?//返回數組的大小

var?f?=?(0..

f?=?f.map?{?$0?*?$0?}

let?c1?=?powf(12194.217,?2.0)

let?c2?=?powf(20.598997,?2.0)

let?c3?=?powf(107.65265,?2.0)

let?c4?=?powf(737.86223,?2.0)

let?num?=?f.map?{?c1?*?$0?*?$0?}

let?den?=?f.map?{?($0?+?c2)?*?sqrtf(($0?+?c3)?*?($0?+?c4))?*?($0?+?c1)?}

let?weights?=?num.enumerated().map?{?(index,?ele)?in

return?1.2589?*?ele?/?den[index]

}

return?weights

}

更新analyse函數中的代碼：

func?analyse(with?buffer:?AVAudioPCMBuffer)?->?[[Float]]?{

let?channelsAmplitudes?=?fft(buffer)

var?spectra?=?[[Float]]()

//1:?創建權重數組

let?aWeights?=?createFrequencyWeights()

for?amplitudes?in?channelsAmplitudes?{

//2：原始頻譜數據依次與權重相乘

let?weightedAmplitudes?=?amplitudes.enumerated().map?{(index,?element)?in

return?element?*?aWeights[index]

}

let?spectrum?=?bands.map?{

//3:?findMaxAmplitude函數將從新的`weightedAmplitudes`中查找最大值

findMaxAmplitude(for:?$0,?in:?weightedAmplitudes,?with:?Float(buffer.format.sampleRate)??/?Float(self.fftSize))?*?5

}

spectra.append(spectrum)

}

return?spectra

}

再次運行項目看看效果，好多了是嗎？

圖6 A計權之后的動畫表現

鋸齒消除

接著是鋸齒過多的問題，手段是將相鄰較長的拉短較短的拉長，常見的辦法是使用加權平均。創建函數highlightWaveform()：

private?func?highlightWaveform(spectrum:?[Float])?->?[Float]?{

//1:?定義權重數組，數組中間的5表示自己的權重

//???可以隨意修改，個數需要奇數

let?weights:?[Float]?=?[1,?2,?3,?5,?3,?2,?1]

let?totalWeights?=?Float(weights.reduce(0,?+))

let?startIndex?=?weights.count?/?2

//2:?開頭幾個不參與計算

var?averagedSpectrum?=?Array(spectrum[0..

for?i?in?startIndex..

//3:?zip作用:?zip([a,b,c],?[x,y,z])?->?[(a,x),?(b,y),?(c,z)]

let?zipped?=?zip(Array(spectrum[i?-?startIndex...i?+?startIndex]),?weights)

let?averaged?=?zipped.map?{?$0.0?*?$0.1?}.reduce(0,?+)?/?totalWeights

averagedSpectrum.append(averaged)

}

//4：末尾幾個不參與計算

averagedSpectrum.append(contentsOf:?Array(spectrum.suffix(startIndex)))

return?averagedSpectrum

}

analyse函數需要再次更新：

func?analyse(with?buffer:?AVAudioPCMBuffer)?->?[[Float]]?{

let?channelsAmplitudes?=?fft(buffer)

var?spectra?=?[[Float]]()

for?amplitudes?in?channelsAmplitudes?{

let?weightedAmplitudes?=?amplitudes.enumerated().map?{(index,?element)?in

return?element?*?weights[index]

}

let?spectrum?=?bands.map?{

findMaxAmplitude(for:?$0,?in:?weightedAmplitudes,?with:?Float(buffer.format.sampleRate)??/?Float(self.fftSize))?*?5

}

//1:?添加到數組之前調用highlightWaveform

spectra.append(highlightWaveform(spectrum:?spectrum))

}

return?spectra

}

圖7 鋸齒少了，波形變得明顯

閃動優化

動畫閃動給人的感覺就好像丟幀一樣。造成這個問題的原因，是因為頻帶的值前后兩幀變化太大，我們可以將上一幀的值緩存起來，然后跟當前幀的值進行...沒錯，又是加權平均！ (⊙﹏⊙)b 繼續開始編寫代碼，首先需要定義兩個屬性：

//緩存上一幀的值

private?var?spectrumBuffer:?[[Float]]?

//緩動系數，數值越大動畫越"緩"

public?var?spectrumSmooth:?Float?=?0.5?{

didSet?{

spectrumSmooth?=?max(0.0,?spectrumSmooth)

spectrumSmooth?=?min(1.0,?spectrumSmooth)

}

}

接著修改analyse函數：

func?analyse(with?buffer:?AVAudioPCMBuffer)?->?[[Float]]?{

let?channelsAmplitudes?=?fft(buffer)

let?aWeights?=?createFrequencyWeights()

//1:?初始化spectrumBuffer

if?spectrumBuffer.count?==?0?{

for?_?in?0..

spectrumBuffer.append(Array(repeating:?0,?count:?frequencyBands))

}

}

//2:?index在給spectrumBuffer賦值時需要用到

for?(index,?amplitudes)?in?channelsAmplitudes.enumerated()?{

let?weightedAmp?=?amplitudes.enumerated().map?{(index,?element)?in

return?element?*?aWeights[index]

}

var?spectrum?=?bands.map?{

findMaxAmplitude(for:?$0,?in:?weightedAmplitudes,?with:?Float(buffer.format.sampleRate)??/?Float(self.fftSize))?*?5

}

spectrum?=?highlightWaveform(spectrum:?spectrum)

//3:?zip用法前面已經介紹過了

let?zipped?=?zip(spectrumBuffer[index],?spectrum)

spectrumBuffer[index]?=?zipped.map?{?$0.0?*?spectrumSmooth?+?$0.1?*?(1?-?spectrumSmooth)?}

}

return?spectrumBuffer

}

再次運行項目，得到最終效果：

結尾

音頻頻譜的動畫實現到此已經全部完成。本人之前對音頻和聲學毫無經驗，兩篇文章涉及的方法理論均參考自互聯網，肯定有不少錯誤，歡迎指正。

參考資料

[1] 維基百科, 倍頻程頻帶, en.wikipedia.org/wiki/Octave…

[2] 維基百科, 響度, ?zh.wikipedia.org/wiki/%E9%9F…

[3] mathworks，A-weighting Filter with Matlab，www.mathworks.com/matlabcentr…

[4] 動畫效果：網易云音樂APP、MOO音樂APP。感興趣的同學可以用卡農鋼琴版音樂和這兩款APP進行對比^_^，會發現區別。作者：potato04

鏈接：https://juejin.im/post/5c26d44ae51d45619a4b8b1e