關于二分法的邊界問題及兩種寫法

二分查找法大家很熟悉了，對于一個有序序列，我們可以通過二分查找法在 $O(logN)$ 的時間內找到想要的元素。但是，在代碼實現的過程中，如果沒有仔細理解清楚，二分法的邊界條件有時會讓人很頭疼，而對邊界條件的妥善處理是很能體現一個人的代碼功底的，也通常是面試官會很關注的一個點。另外，大佬的題解中的二分法代碼也總有幾處小細節不同，但是大佬的代碼都是怎么測都沒問題的，自己卻總因為某處細節沒有處理好而出現問題。

實際上，二分法通常有兩種細節略有不同的實現方式：左閉右閉和左閉右開，本文將簡單介紹這兩種實現方式，并指出他們之間的不同及適用情況，希望也能夠幫助大家徹底理解二分法，從此不再會因為邊界條件問題出錯。

題目

我們先給定題目要求，就通過 LeetCode 上的一道二分法的題目為例：704. 二分查找。

給定一個 n 個元素有序的（升序）整型數組 nums 和一個目標值 target ，寫一個函數搜索 nums 中的 target，如果目標值存在返回下標，否則返回 -1。

示例 1:

輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中并且下標為 4

示例 2:

輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1

提示：

• 你可以假設 nums 中的所有元素是不重復的。
• n 將在 [1, 10000]之間。
• nums 的每個元素都將在 [-9999, 9999]之間。

給定的函數簽名 (C++) 是這樣的：

class Solution {
public:int search(vector<int>& nums, int target) {}
};

說明：以下兩節講解參考自代碼隨想錄。

左閉右閉

第一種寫法，我們定義 target 是在一個在左閉右閉的區間里，也就是 [left, right] （這個很重要非常重要）。

區間的定義這就決定了二分法的代碼應該如何寫，因為定義target在[left, right]區間，所以有如下兩點：

• while (left <= right) 要使用 <= ，因為left == right是有意義的，所以使用 <=
• if (nums[middle] > target) right 要賦值為 middle - 1，因為當前這個nums[middle]一定不是target，那么接下來要查找的左區間結束下標位置就是 middle - 1

例如在數組：1,2,3,4,7,9,10中查找元素2，如圖所示：

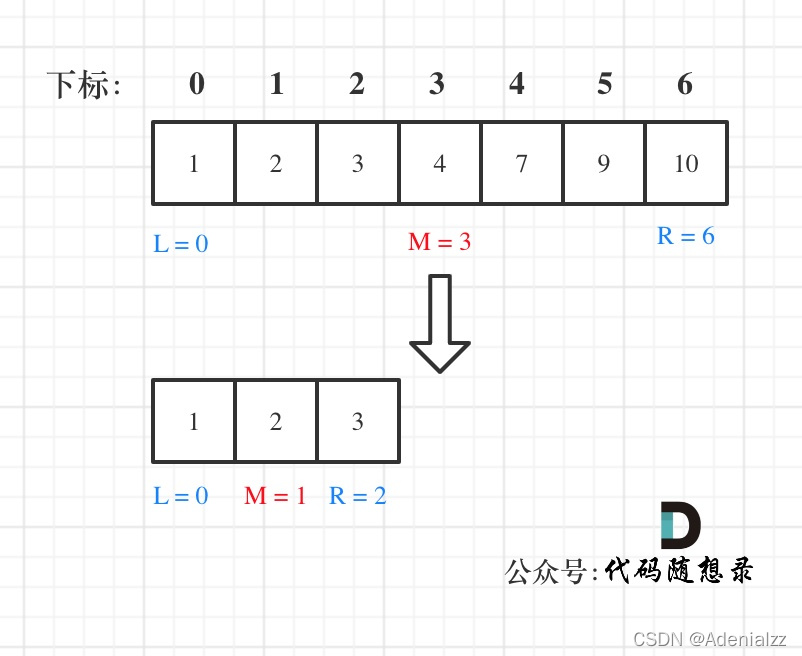
代碼：

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1; // 定義target在左閉右閉的區間里，[left, right]while (left <= right) { // 當left==right，區間[left, right]依然有效，所以用 <=int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2if (nums[middle] > target) {right = middle - 1; // target 在左區間，所以[left, middle - 1]} else if (nums[middle] < target) {left = middle + 1; // target 在右區間，所以[middle + 1, right]} else { // nums[middle] == targetreturn middle; // 數組中找到目標值，直接返回下標}}// 未找到目標值return -1;}
};

左閉右開

如果說定義 target 是在一個在左閉右開的區間里，也就是[left, right) ，那么二分法的邊界處理方式則截然不同。

有如下兩點：

• while (left < right)，這里使用 < ,因為left == right在區間[left, right)是沒有意義的
• if (nums[middle] > target) right 更新為 middle，因為當前nums[middle]不等于target，去左區間繼續尋找，而尋找區間是左閉右開區間，所以right更新為middle，即：下一個查詢區間不會去比較nums[middle]

在數組：1,2,3,4,7,9,10中查找元素2，如圖所示：（注意和方法一的區別）

代碼：

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size(); // 定義target在左閉右開的區間里，即：[left, right)while (left < right) { // 因為left == right的時候，在[left, right)是無效的空間，所以使用 <int middle = left + ((right - left) >> 1);if (nums[middle] > target) {right = middle; // target 在左區間，在[left, middle)中} else if (nums[middle] < target) {left = middle + 1; // target 在右區間，在[middle + 1, right)中} else { // nums[middle] == targetreturn middle; // 數組中找到目標值，直接返回下標}}// 未找到目標值return -1;}
};

搜索插入的位置：不大于target的最大索引

完整功能的二分法除了查找之外，還應該在沒有查找到 target 元素時返回 target 應該插入的位置，為接下來可能的插入操作提供便利。

35. 搜索插入位置

注意本題要求保證給定數組是嚴格單增的，即不存在相等的元素，如果存在相等的元素如 [1,2,3,3,5] 這種情況在插入 3 時就會有多個合理的插入位置。

版本一：左閉右閉

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = (right - left) / 2 + left;if (nums[mid] > target) right = mid - 1;else if (nums[mid] < target) left = mid + 1;else return mid;}return left;		// 注意}
};

版本二：左閉右開

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size();while (left < right) {int mid = (right - left) / 2 + left;if (nums[mid] > target) right = mid;else if (nums[mid] < target) left = mid + 1;else return mid;}return right;		// 注意}
};

在排序數組中搜索元素的第一個和最后一個位置

34. 在排序數組中查找元素的第一個和最后一個位置

由于數組已經排序，因此整個數組是單調遞增的，我們可以利用二分法來加速查找的過程。

考慮 $target$ 開始和結束位置，其實我們要找的就是數組中「第一個等于 $target$ 的位置」（記為 $leftIdx$ ）和「第一個大于 $target$ 的位置減一」（記為 $rightIdx$ ）。

二分查找中，尋找 $leftIdx$ 即為在數組中尋找第一個大于等于 $target$ 的下標，尋找 $rightIdx$ 即為在數組中尋找第一個大于 $target$ 的下標，然后將下標減一。兩者的判斷條件不同，為了代碼的復用，我們定義 binarySearch(nums, target, lower) 表示在 $nums$ 數組中二分查找 $target$ 的位置，如果 $lower$ 為 $true$，則查找第一個大于等于 $target$ 的下標，否則查找第一個大于 $target$ 的下標。

最后，因為 $target$ 可能不存在數組中，因此我們需要重新校驗我們得到的兩個下標 $leftIdx$ 和 $rightIdx$，看是否符合條件，如果符合條件就返回 $[leftIdx,rightIdx]$，不符合就返回 $[?1,?1]$。

class Solution {
private:int binSearch(vector<int>& nums, int target, bool lower) {int left = 0, right = nums.size() - 1;int res = nums.size();while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] > target || (lower && nums[mid] >= target)) {right = mid - 1;res = mid;}else left = mid + 1;}return res;}
public:vector<int> searchRange(vector<int>& nums, int target) {int left = binSearch(nums, target, true);int right = binSearch(nums, target, false) - 1;if (left <= right && nums[left] == target && nums[right] == target && right <= nums.size()) return {left, right};else return {-1, -1};}
};

Ref：

https://leetcode-cn.com/problems/binary-search

https://leetcode-cn.com/problems/search-insert-position/

https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html#%E6%80%9D%E8%B7%AF