圖像預處理之warpaffine與雙線性插值及其高性能實現

視頻講解：https://www.bilibili.com/video/BV1ZU4y1A7EG

代碼Repo：https://github.com/shouxieai/tensorRT_Pro

本文為視頻講解的個人筆記。

warpaffine矩陣變換

對于坐標點的變換，我們通常考慮的是旋轉、縮放、平移這三種變換。例如將點 $P(x,y)$ 旋轉 $\theta$ 度，縮放 $scale$ 倍，平移 $ox,oy$ 。warpaffine 將坐標點的旋轉、縮放、平移三種操作集成為一個矩陣乘法運算。

旋轉變換

我們先來看旋轉，如圖所示，我們要將點 $P(x,y)$ 旋轉到點 $P^{\prime }(x^{\prime },y^{\prime })$ ，推導的過程很簡單，我們要求的就是 $x^{\prime },y^{\prime }$ 兩點的坐標，將其轉換為 $m\times cos(\theta +\alpha )$ 和 $m\times sin(\theta +\alpha )$ ，再用公式展開，即得結果（詳見圖中公式）：

$$\left\{\begin{array}{r}{x}^{\prime }\\ y^{\prime }\end{array}\right\}=\left\{\begin{array}{rc}cos(\theta )& ?sin(\theta )\\ sin(\theta )& cos(\theta )\end{array}\right\}\left\{\begin{array}{r}x\\ y\end{array}\right\}$$
再考慮到我們在圖像處理時的坐標系（如在 OpenCV 中的坐標系、常見目標檢測的坐標系等）通常是原點在左上角，因此應該為：

$$\left\{\begin{array}{r}{x}^{\prime }\\ y^{\prime }\end{array}\right\}=\left\{\begin{array}{rc}cos(\theta )& sin(\theta )\\ ?sin(\theta )& cos(\theta )\end{array}\right\}\left\{\begin{array}{r}x\\ y\end{array}\right\}$$
將旋轉變換的矩陣記為 $R$ ，則 $P^{\prime }=RP$

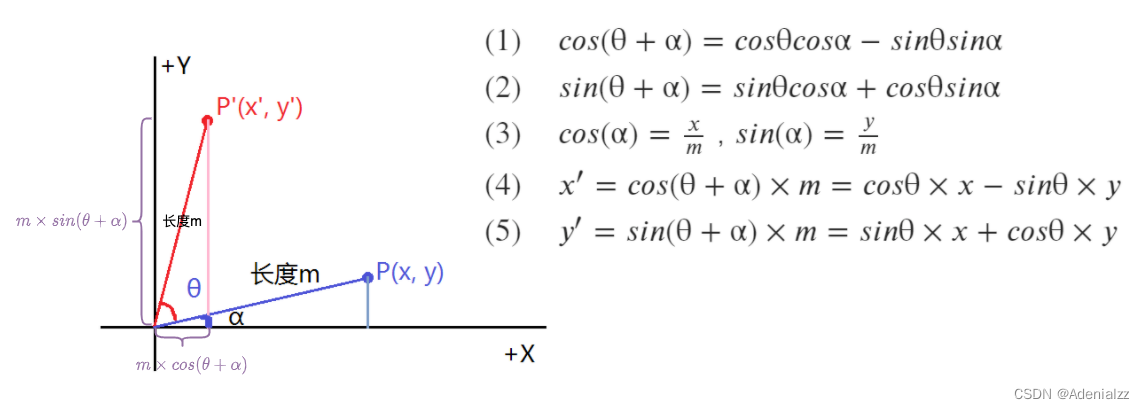
縮放變換

縮放變換比較簡單，兩坐標直接乘以縮放系數 $scale$ 即可：

$$\begin{gathered} x^{\prime }=x\times scale \\ {y}^{\prime }=y\times scale \end{gathered}$$
寫成矩陣形式即：

$$\left\{\begin{array}{r}{x}^{\prime }\\ y^{\prime }\end{array}\right\}=\left\{\begin{array}{rc}scale& 0\\ 0& scale\end{array}\right\}\left\{\begin{array}{r}x\\ y\end{array}\right\}$$
將縮放變換的變換矩陣記為 $S$，則：
$$P^{\prime }=SP$$
則旋轉+縮放可以通過矩陣相乘寫到同一個矩陣中：
$$\left\{\begin{array}{r}{x}^{\prime }\\ y^{\prime }\end{array}\right\}=\left\{\begin{array}{rc}cos(\theta )\times scale& sin(\theta )\times scale\\ ?sin(\theta )\times scale& cos(\theta )\times scale\end{array}\right\}\left\{\begin{array}{r}x\\ y\end{array}\right\}$$
即：$P^{\prime }=SRP$

注意旋轉和縮放順序是隨意的，不影響結果，這也可以通過代碼來驗證：

import numpy as nptheta = 0.8
scale = 2
rot = np.array([[np.cos(theta), np.sin(theta)],[-np.sin(theta), np.cos(theta)]
])sca = np.array([[scale, 0],[0, scale]
])print(np.allclose(rot @ sca, sca @ rot))
# 輸出：True

平移變換

平移變換可以表示為：
$$\begin{gathered} x^{\prime }=x+ox \\ {y}^{\prime }=y+oy \end{gathered}$$
矩陣形式：
$$\left\{\begin{array}{r}{x}^{\prime }\\ y^{\prime }\end{array}\right\}=\left\{\begin{array}{rc}1& 0\\ 0& 1\end{array}\right\}\left\{\begin{array}{r}x\\ y\end{array}\right\}+\left\{\begin{array}{r}ox\\ oy\end{array}\right\}$$
可以發現，平移變換直接寫成矩陣形式，已經不是單純的矩陣相乘了，而是多了一個很麻煩的相加的操作。這就很難與我們之前的縮放+旋轉的操作合并到一起，該怎么辦呢？

我們可以增加一個維度，將二維的非齊次的形式轉換為三維的齊次的形式，即這個知乎回答中所提到的：增加一個維度之后，就可以在高維度通過線性變換來完成低維度的放射變換。（該回答將放射變換講的很形象，推薦閱讀）。

那么我們增加一維 $(x,y,w)$，從而將點 $P$ 表示為 $P(\frac{x}{w},\frac{y}{w},1)$ ，這樣平移變換就也可以表示為齊次矩陣乘的形式：

$$?\begin{array}{r}{x}^{\prime }\\ y^{\prime }\\ w\end{array}?=?\begin{array}{rcc}1& 0& ox\\ 0& 1& oy\\ 0& 0& 1\end{array}??\begin{array}{r}x\\ y\\ 1\end{array}?$$
最后我們得到縮放+旋轉+平移變換的矩陣表示（注意平移與縮放、旋轉的順序是不能隨意調換的）：

$$?\begin{array}{r}{x}^{\prime }\\ y^{\prime }\\ w\end{array}?=?\begin{array}{rcc}cos(\theta )\times scale& sin(\theta )\times scale& ox\\ ?sin(\theta )\times scale& cos(\theta )\times scale& oy\\ 0& 0& 1\end{array}??\begin{array}{r}x\\ y\\ 1\end{array}?$$
將平移變換的變換矩陣記為 $R$ ，則：$P^{\prime }=TSRP$ ，可以將整個 warpaffine 三個變換操作的矩陣記為 $M$ ，即：$M=TSR,P^{\prime }=MP$ 。

warpaffine矩陣變換的反變換

• 旋轉矩陣的逆矩陣，即是其轉置：$R^{?1}=R^T$
• 整個 warp affine 的三個變換求反變換，對整個變換矩陣求逆即可：$P^{\prime }=MP,P=M^{?1}{P}^{\prime }$

目標檢測中的常用預處理

在目標檢測中，我們的預處理通常是先對圖像進行等比縮放，然后居中，多余部分填充，就類似下圖所展示的。

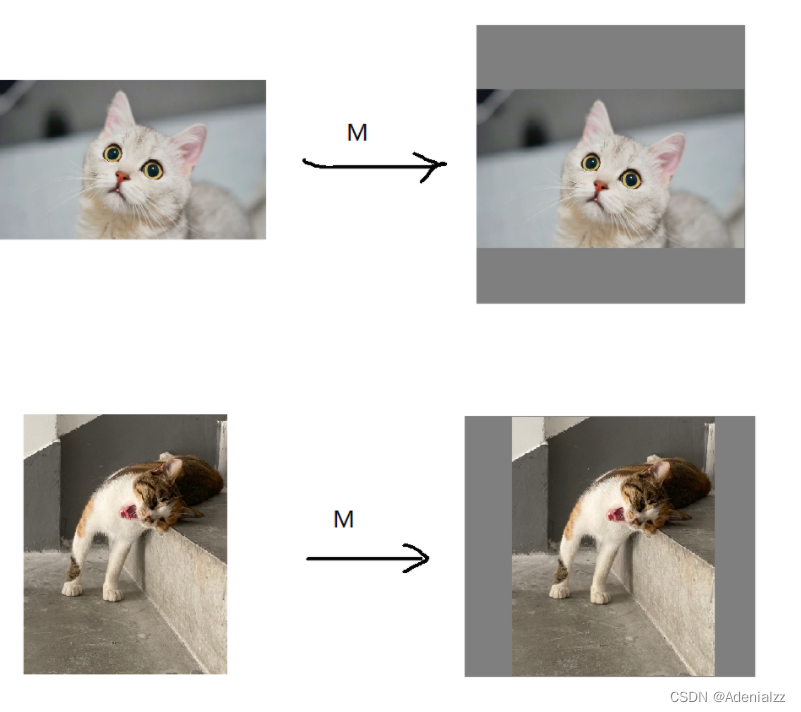
我們將這個過程分為三個步驟：

1. 等比縮放，矩陣 $S$ 實現

2. 將圖片中心平移到左上坐標原點，矩陣 $O$ 實現

3. 將圖片平移到目標位置的重心，矩陣 $T$ 實現

三步拆分法，看似麻煩了一點，實際上可以方便我們后續可能會需要到的更復雜的變換（比如在 $O$ 平移后加入旋轉變換），并且便于記憶。

三步拆分法的矩陣表達：$P^{\prime }=TOSP$ 。

我們直接寫出具體的矩陣：
$$\begin{gathered} scale=min(\frac{Dst.width}{Origin.width},\frac{Dst.height}{Origin.height}) \\ M=\left\{\begin{array}{llc}scale& 0& ?\frac{scale\times Origin.width}{2}+\frac{Dst.width}{2}\\ 0& scale& ?\frac{scale\times Origin.height}{2}+\frac{Dst.height}{2}\end{array}\right\} \end{gathered}$$

$$\left\{\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right\}=\left\{\begin{array}{llc}scale& 0& ?\frac{scale\times Origin.width}{2}+\frac{Dst.width}{2}\\ 0& scale& ?\frac{scale\times Origin.height}{2}+\frac{Dst.height}{2}\end{array}\right\}?\begin{array}{l}x\\ y\\ 1\end{array}?$$

逆變換：
$$\begin{gathered} k=scale \\ b1=?\frac{scale\times Origin.width}{2}+\frac{Dst.width}{2} \\ b2=?\frac{scale\times Origin.height}{2}+\frac{Dst.height}{2} \\ {x}^{\prime }=kx+b1 \\ {y}^{\prime }=ky+b2 \\ x=\frac{x^{\prime }?b1}{k}=x^{\prime }\times \frac{1}{k}+(?\frac{b1}{k}) \\ y=\frac{y^{\prime }?b2}{k}=y^{\prime }\times \frac{1}{k}+(?\frac{b2}{k}) \\ {M}^{?1}=\left\{\begin{array}{llc}\frac{1}{k}& 0& ?\frac{b1}{k}\\ 0& \frac{1}{k}& ?\frac{b2}{k}\end{array}\right\} \end{gathered}$$

warpaffine正逆變換代碼實驗

TODO

雙線性插值

線性插值

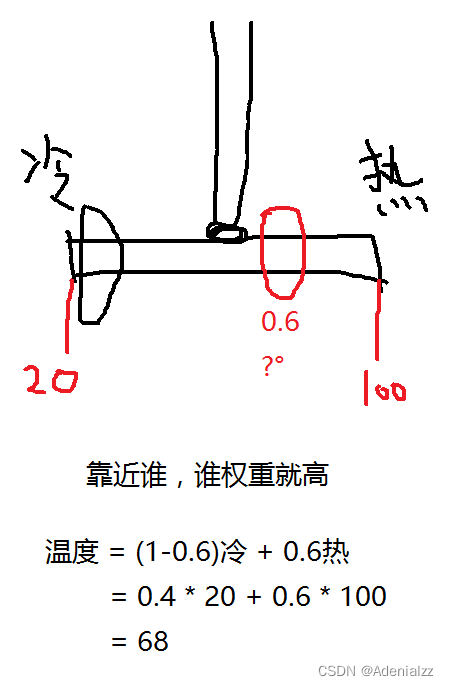
距離目標點越遠，影響就越小，因此權重是對面的距離占比。

如目標點距離冷水 0.6，距離熱水 0.4，則冷水權重為 0.4 ，熱水權重為 0.6 。

p0 = 20    # 冷水
p1 = 100   # 熱水
pos = 0.6  # 應該多少度value = (1 - pos) * p0 + pos * p1
print(value)

雙線性插值

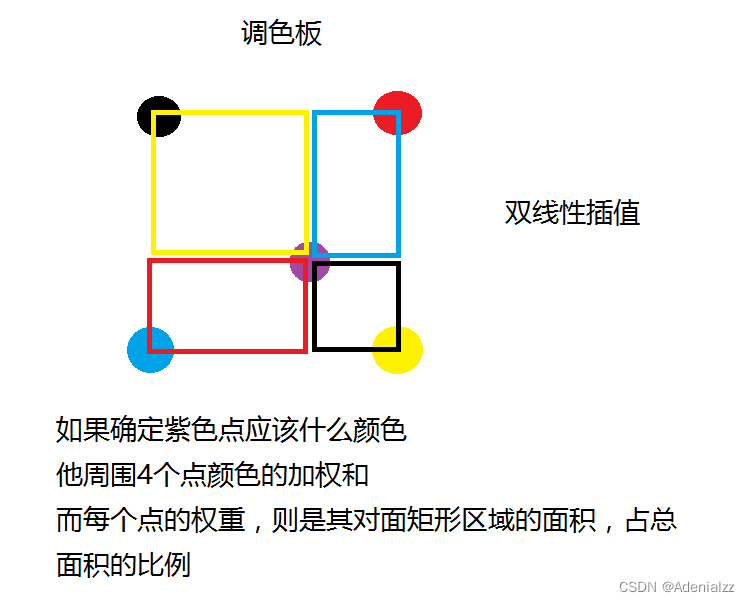
線性插值的二維版本，原理一直，只是權重從計算長度占比改為計算面積占比。

調色板，紅點對目標點（紫點）的影響權重即為對面的面積（紅框面積）占總面積的比例。

高性能實現

為什么高性能？

• 我們在操作每個像素的過程中，可以將模型需要的像素級預處理（如減均值除標準差、除以255、BGR通道轉換等）一并做了，避免多個操作分開來反復對每個像素進行循環訪問這種低效行為。
• warpaffine 極其適合通過 cuda 核函數進行 GPU 加速。可以參考 repo 中的 preprocess_kernel.cu 。完整代碼比較長這里就不放了。
• 以下是 warpaffine 雙線性插值的 Python 實現，供參考：

def pyWarpAffine(image, M, dst_size, constant=(0, 0, 0)):# 注意輸入的M矩陣格式，是Origin->Dst# 而這里需要的是Dst->Origin，所以要取逆矩陣M = cv2.invertAffineTransform(M)constant = np.array(constant)ih, iw   = image.shape[:2]dw, dh   = dst_sizedst      = np.full((dh, dw, 3), constant, dtype=np.uint8)irange   = lambda p: p[0] >= 0 and p[0] < iw and p[1] >= 0 and p[1] < ihfor y in range(dh):for x in range(dw):homogeneous = np.array([[x, y, 1]]).Tox, oy = M @ homogeneouslow_ox = int(np.floor(ox))low_oy = int(np.floor(oy))high_ox = low_ox + 1high_oy = low_oy + 1# p0     p1#      o# p2     p3pos = ox - low_ox, oy - low_oyp0_area = (1 - pos[0]) * (1 - pos[1])p1_area = pos[0] * (1 - pos[1])p2_area = (1 - pos[0]) * pos[1]p3_area = pos[0] * pos[1]p0 = low_ox, low_oyp1 = high_ox, low_oyp2 = low_ox, high_oyp3 = high_ox, high_oyp0_value = image[p0[1], p0[0]] if irange(p0) else constantp1_value = image[p1[1], p1[0]] if irange(p1) else constantp2_value = image[p2[1], p2[0]] if irange(p2) else constantp3_value = image[p3[1], p3[0]] if irange(p3) else constantdst[y, x] = p0_area * p0_value + p1_area * p1_value + p2_area * p2_value + p3_area * p3_value# 交換bgr  rgb# normalize ->  -mean /std# 1行代碼實現normalize , /255.0# bgr bgr bgr -> bbb ggg rrr# focus# focus offset, 1行代碼實現focusreturn dstcat1 = cv2.imread("cat1.png")
#acat1_cv, M, inv = align(cat1, (100, 100))
M = cv2.getRotationMatrix2D((0, 0), 30, 0.5)
acat1_cv = cv2.warpAffine(cat1, M, (100, 100))
acat1_py = pyWarpAffine(cat1, M, (100, 100))plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
plt.title("OpenCV")
plt.imshow(acat1_cv[..., ::-1])plt.subplot(1, 2, 2)
plt.title("PyWarpAffine")
plt.imshow(acat1_py[..., ::-1])