
本文始發于個人公眾號: TechFlow
題意
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Link: https://leetcode.com/problems/longest-palindromic-substring/
翻譯
給定一個字符串s,要求它當中的最長回文子串。可以假設s串的長度最大是1000。
樣例
Example 1:
Input: "babad"Output: "bab"Note: "aba" is also a valid answer.Example 2:
Input: "cbbd"Output: "bb"分析
雖然LeetCode里給這道題的難度是Medium,但實際上并不簡單,我們通過自己思考很難想到最佳解法。
我們先把各種算法放在一邊,先從最簡單的方法開始。最簡單的方法當然是暴力枚舉,但是這道題和之前的字符串問題不同。
我們在暴力枚舉的時候,并不需要枚舉所有的起始位置,再判斷這個子串是否回文。實際上我們可以利用回文串兩邊相等的性質,直接枚舉回文串的中心位置,如果兩邊相等就往兩邊延伸。這樣我們最多需要枚舉n個回文中心,每次枚舉最多遍歷n次。所以最終的復雜度是O(n^2)。
有經驗的同學看到這個復雜度就能反應過來,這明顯不是最優解法。但是對于當前問題,暴力枚舉固然不是最佳解法,但其實也算得上是不錯了,并沒有我們想的那么糟糕,不信的話,我們來看另一個看起來高端很多的解法。
動態規劃(DP)
這道題中利用回文串的性質還有一個trick,對于一個字符串S,如果我們對它進行翻轉,得到S_,顯然它當中的回文子串并不會發生變化。所以如果我們對翻轉前后的兩個字符串求最長公共子序列的話,得到的結果就是回文子串。
算法導論當中對這個問題的講解是使用動態規劃算法,即是對于字符串S中所有的位置i和S_中所有的位置j,我們用一個dp數組記錄下以i和j結尾的S和S_的子串能夠組成的公共子序列的最大的結果。
顯然,對于i=0,j=0,dp[i][j] = 0(假設字符串下標從1開始)
我們寫出DP的代碼:
for
我們不難觀察出來,這種解法的復雜度同樣是O(n^2)。并且空間復雜度也是O(n^2),也就是說我們費了這么大勁,并沒有起到任何優化。所以從這個角度來看,暴力搜索并不是這題當中很糟糕的解法。
分析到了這里,也差不多了,下面我們直接進入正題,這題的最佳解法,O(n)時間內獲取最大回文子串的曼徹斯特算法。
曼切斯特算法
回文串除了我們剛剛提到的性質之外,還有一個性質,就是它分奇偶。簡而言之,就是回文串的長度可以是奇數也可以是偶數。如果是奇數的話,那么回文串的回文中心就是一個字符,如果是偶數的話,它的回文中心其實是落在兩個字符中間。
舉個例子:
ABA和ABBA都是回文串,前者是奇回文,后者是偶回文。
這兩種情況不一致,我們想要一起討論比較困難,為了簡化問題,我們需要做一個預處理,將所有的回文串都變成奇回文。怎么做呢,其實很簡單,我們在所有兩個字符當中都插入一個特殊字符#。
比如:
abba -> #a#b#b#a#
這樣一來,回文中心就變成中間的#了。我們再來看原本是奇回文的情況:
aba -> #a#b#a#
回文中心還是在b上,依然還是奇回文。
預處理的代碼:
def 曼切斯特算法用到三個變量,分別是數組p,idx和mr。我們接下來一個一個介紹。
首先是數組radis,它當中存在的是每個位置能構成的最長回文串的半徑。注意,這里不是長度,是半徑。
我們舉個例子:
字符串S # a # b # b # a #
radis 1 2 1 2 5 2 1 2 1
我們先不去想這個radis數組應該怎么求,我們來看看它的性質。
首先,i位置的回文串的半徑是radis[i],那么它的長度是多少?很簡單: radis[2] * 2 - 1。那么,這個串中去掉#之后剩下的長度是多少?也就是說預處理之前的長度是多少?
答案是radis[i] - 1,推算也很簡單,總長度是radis[i] * 2 - 1,其中#比字母的數量多一個,所以原串的長度是(radis[i] * 2 - 1 - 1)/2 = radis[i] - 1。
也就是說原串的長度和radis數組就算是掛鉤了。
idx很好理解,它就是指的是數組當中的一個下標,最后是mr,它是most_right的縮寫。它記錄的是在當前位置i之前的回文串所向右能延伸到的最遠的位置。
聽起來有些拗口,我們來看個例子:

此時i小于mr,mr對應的回文中心是id。那么i在id的回文范圍當中,對于i而言,我們可以獲取到它關于id的對稱位置:id * 2 - i,我們令它等于i_。知道這個對稱的位置有什么用呢?很簡單,我們可以快速的確定radis[i]的下界。在遍歷到i的時候,我們已經有了i_位置的結果。通過i_位置的結果,我們可以推算i位置的范圍。
radis[i] >= min(radis[i_], mr-i)
為什么是這個結果呢?
我們把情況寫全,假設mr-i > radis[i_]。那么i_位置的回文串全部都落在id位置的回文串里。這個時候,我們可以確定radis[i]=radis[i_]。為什么呢?
因為根據對稱原理,如果以i為中心的回文串更長的話,我們假設它的長度是radis[i_]+1。會導致什么后果呢?如果這個發生,那么根據關于id的對稱性,這個字符串關于id的對稱位置也是回文的。那么radis[i_1]也應該是這么多才對,這就構成了矛盾。如果你從文字描述看不明白的話,我們來看下面這個例子:
S: c a b c b d b c b a
cradis: x_ i_ 5 i x在這個例子當中,mr-i=5,radis[i_]=2。所以mr - i > radis[i_]。如果radis[i]=3,那么x的位置就應該等于id的位置,同理根據對稱性,x_的位置也應該等于id的位置。那么radis[i_]也應該是3。這就和它等于2矛盾,所以這是不可能出現的,在mr距離足夠遠的情況下,radis[i_]的值限制了i位置的可能性。
我們再來看另一種情況,如果mr - i < radis[i_]時會怎么樣呢?
在這種情況下,由于mr距離i太近,導致i對稱位置的半徑無法在i位置展開。但是mr的右側可能還存在字符,這些字符可以構成新的回文嗎?
字符串S XXXXXXXXSXXXXXXXXXXXXXXX
radis i_ id i mr
也就是說S[mr+1]會和S[i*2-mr-1]的位置相同嗎?
其實我們可以不用判斷就可以知道答案,答案是不會。
我們來看圖:
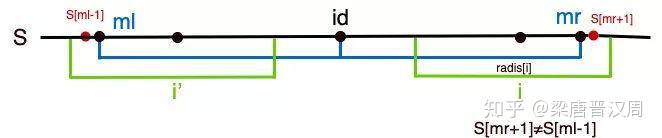
根據對稱性,如果mr+1的位置對于i可以構成新的對稱。由于radis[i_] > mr-i,也就是說對于i_位置而言,它的對稱范圍能夠輻射到mr對稱點的左邊。我們假設這個地方的字母是a,根據對稱性,我們可以得出mr+1的位置也應該是a。如此一來,這兩個a又能構成新的對稱,那么id位置的半徑就可以再拓展1,這就構成了矛盾。所以,這種情況下,由于mr-i的限制,使得radis[i]只能等于mr - i。
那什么情況下i位置的半徑可以繼續拓展呢?
只有mr - i == radis[i_]的時候,id構成的回文串的左側對于i_可能構不成新的回文,但是右側卻存在這種可能性。

在上圖這個例子當中,i_的位置的回文串向左只能延伸到ml,因為ml-1的位置和關于i_對稱的位置不相等。對于mr的右側,它完全可以既和i點對稱,又不會影響raids[id]的正確性。這個時候,我們就可以通過循環繼續遍歷,拓展i位置的回文串。
整個過程的分析雖然很多,也很復雜,但是寫成代碼卻并不多。
# 初始化
到這里,曼切斯特算法就算是實現完了。雖然我們用了這么多篇幅去介紹它,可是真正寫出來,它只有幾行代碼而已。不得不說,實在是非常巧妙,第一次學習可能需要反復思考,才能真正理解。
不過我們還有一個問題沒有解決,為什么這樣一個兩重循環的算法會是O(n)的復雜度呢?
想要理解這一點,需要我們拋開所有的虛幻來直視本質。雖然我們并不知道循環進行了多少次,但是有兩點可以肯定。通過這兩點,我們就可以抓到復雜度的本質。
第一點,mr是遞增的,只會變大,不會減小。
第二點,mr的范圍是0到n,每次mr增加的數量就是循環的次數。
所以即使我們不知道mr變化了多少次,每次變化了多少,我們依然可以確定,這是一個O(n)的算法。
到這里,文章的內容就結束了,如果喜歡的話,請點個關注吧~









是啥意思?...)










