一、問題描述

給定n種物品和一個背包。物品i的質量Wi，其價值Vi，背包的容量為c。問如何選擇裝入背包中的物品，使得裝入背包中的物品總價值最大？

二、解題思想

? ? ? ? 01背包和最長公共子序列都是動態規劃題目中求最優解的問題，不同在于，01背包問題，即使發現物品可以放入背包，但是在采取放或者不放的措施時，還要進行選擇。（這就是保證最優解的條件）

? ? ? ? 我們先根據題意有如下假設：假設物品的種類和背包的容量是變化的，是逐漸增多的。我們每個不同容量的背包的最大價值，建立在先前背包最大價值的基礎上。例如：背包容量為5的最優解，建立在背包容量為4的最優解的基礎上。

? ? ? ? 既然容量和物品種類是變化的，那么我們建立一個二維數組（下文均稱最佳價值表），橫向代表背包容量，縱向代表物品種類，將每個不同容量的背包的最優解記錄在最佳價值表里（這個最佳價值表記錄的是滿足題意的不同背包容量的最優解），如下圖所示。由此正式開始思解題算法：思考遞推式。

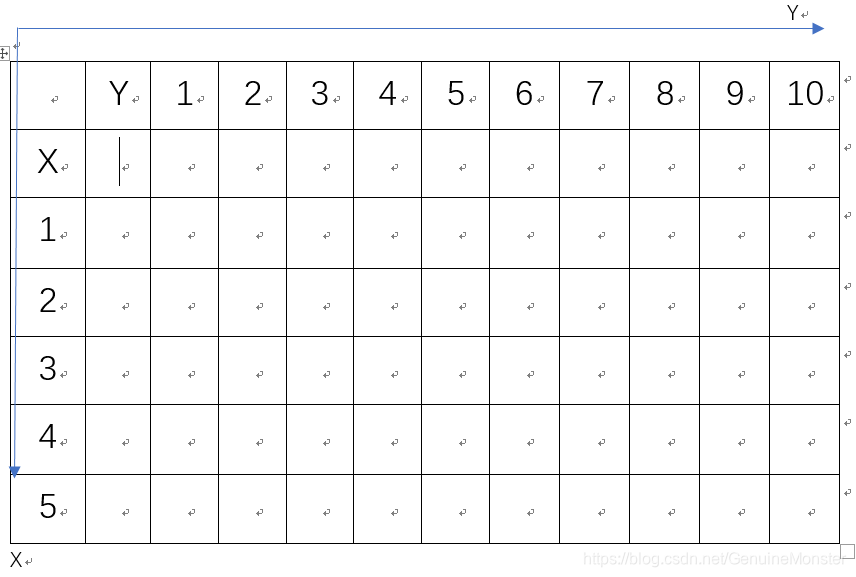
? ? ? ?依照假設，就會得出如下情況：

A、當只有0種物品時，無論背包的容量是多少，背包內物品的總價值都為0（因為沒有東西可放）；當物品的種類很多時，但是背包的容量為0，背包內物品的總價值仍然為0（因為放不進去啊！）所以這個最佳價值表的第0行，第0列都是“0”，其中V[0][0]=0,不是因為我在程序中按照上述賦值為0，其真實原因是：只要是宏變量，聲明在頭文件下的變量，其初值都會自動為0。上述內容相當于對這個最佳價值表做了一個初始化，如下圖所示：

B、當物品的種類和背包容量按照上圖遞增時，就會又出現一種情況：物品不能放入背包（因為物品的質量大于當前背包可容納的質量）、物品能放入背包。

C、物品能放入背包也要分兩種：物品要放入、物品不放入。那么可能你要提問了，為什么物品能裝入但是卻不選擇裝入呢？

因為我們這個二維數組存儲的是背包的最佳價值表。這個物品雖然能放到背包內，但是如果它的體積過大，放入后勢必會影響后續的物品放入，導致此最佳價值表違反了其“最佳”二字。如果第?個物品沒有裝入背包，則背包中物品價值就等于把前??1個物品裝入容量為?的背包中所取得的價值; 如果把第?個物品裝入背包，則背包物品的價值等于第??1個物品裝入容量為??weight[?]的背包中的價值加上第?個物品的價值value[?]。

綜上：

A、V[i][0]=V[0][j]=0? ? ? ?//簡單初始化

B、V[i][j]=V[i-1][j]? ? ? ? ? //物品不能放入

C、V[i][j]=max(v[i-1][j-weight[i]]+value[i],v[i-1][j])? ?//物品能放入

表達式詳細解析：

看到這，有的讀者就會有很多問題，我來以一問一答的形式讓大家更加來了解這道題目的解題思想：

Q1：為什么表達式中每次用當前背包的總容量和新出現的物品的質量作比較，而不是用背包剩余的容量與新出現的物品的質量作比較？

A1：這個問題也是我接觸動態規劃問題之初提過的一個問題。01背包是典型的動態規劃問題，既然是動態規劃問題，那么就要動起來，整個問題中，動就只有一個——物品放入背包中。你可以設想一下，假設你在實際操作的時候，雖然給出的物品很多，但因為你目光有限，所以看到的東西也是一個一個進入眼簾。你可能會先將一個物品放入背包，但是因為后來出現了又小、價值又高的物品，你在權衡之后，可能又得把之前放入的這個物品掏出，騰出空間來放當前這個質量小、價值高的物品·······說了這么多鋪墊，可能有的人已經明白了：這道題的關注點只在于背包能放得下還是放不下，而不是背包放進一些東西之后剩余的空間放的下還是放不下。這個其實直接可以從上述C的表達式可以看出，即：發現物品可放入的時候，你需要以背包的總價值作為衡量依據，到底是放入價值更高了（此時有的人可能會問了，難道物品放入背包后價值還會降低？因為放入物品的時候，需要騰出一定的空間，這就需要拿出背包里的物品，所以放入物品價值不一定更高）還是不放價值更高了，所以用一個max函數來比較。如果發現放入價值高，那就得騰出空間（用最佳價值表的縱軸坐標）

Q2：做這類問題的時候，有什么秘訣沒有？

A2：1、既然是動態問題，那么我們的大腦就得靈活，而且得聯系實際情況，把大問題化成簡單的小問題。計算機是一個很傻的處理機器，重復做著相同的工作，唯一的優點就是快，我們需要做的事情就是告訴他應該做什么事情，做的次數等，其他的就不需要多想了。?2、第二點就是不要多想，直接推導遞推式，然后求解，就像Q1的那種問題就不要多加考慮了。

三、具體實現

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;
int V[100][100];//用來存儲背包的最大價值
int weight[100]; //存儲物品的重量
int value[100];//存儲物品的價值
int state[100];//存儲物品的選取狀態
int max(int a,int b)//比較價值大小函數
{if (a>=b)return a;else return b;
}
int KnapSack(int n,int weight[],int value[],int state[],int capacity)//動態規劃求解函數
{int i,j;//循環變量//V[0][0] = 0;for (i=1;i<=n;i++)//當j=0時(j代表背包容量)，0容量什么都裝不進去，所以V[i][j]=0;V[i][0]=0;for (j=1;j<=capacity;j++)//當i=0時，代表沒有物品，即使背包容量再大，其V[0][j]=0;V[0][j]=0;//#####下面進行判斷######for (i=1;i<=n;i++)//i代表物品，j代表背包容量{//j代表背包的容量，將其從0逐步增加到輸入的背包容量，相當于以背包的容量為限制，一步一步求得最大價值的方法。for (j=1;j<=capacity;j++){if(j<weight[i])//表示該物品?不能裝入背包。V[i][j]=V[i-1][j];//表明此處的價值等于前i-1個物品裝入的價值。else//第?個物品的重量小于背包的容量后就會有兩種情況，一種放入，一種不放入，求這兩種情況中Value最大的。V[i][j]=max(V[i-1][j],V[i-1][j-weight[i]]+value[i]);//如果把第?個物品裝入背包，則背包物品的價值等于第??1個物品裝入容量位??weight[?]的背包中的價值加上第?個物品的價值value[?]//如果第?個物品沒有裝入背包，則背包中物品價值就等于把前??1個物品裝入容量為?的背包中所取得的價值。}}j=capacity;//為標記“哪件物品放入背包”做準備for(i=n;i>=1;i--)//標記選出的物品函數{if(V[i][j]>V[i-1][j]){state[i]=1;//1表示選中j=j-weight[i];}elsestate[i]=0;//0表示未選中}printf("選中的物品是:");for(i=1;i<=n;i++)printf("%d ",state[i]);printf("\n");cout<<"V[i][j]中的數字是：\n";for(int i=0;i<=n;i++){for(int j=0; j<=capacity;j++){printf("%3d", V[i][j]);if (j == capacity){printf("\n");}}}return V[n][capacity];
}
int main()
{int s;//獲得的最大價值int n = 0;//用于循環輸入cout<< "請輸入物品的個數：";cin >> n;cout << "請輸入物品對應的質量：";for (int i = 1; i <= n; i++)cin >> weight[i];cout << "請輸入物品對應的價值：";for (int i = 1; i <=n; i++)cin >> value[i];cout << "請輸入背包最大容量：";int capacity;cin >> capacity;//背包最大容量s = KnapSack(n, weight, value, state, capacity);cout<<"最大物品價值為:"<<s<<endl;system("pause");return 0;
}

其中有一個for循環用來找出哪些東西被放入背包中，1代表放入，0代表沒放入。?

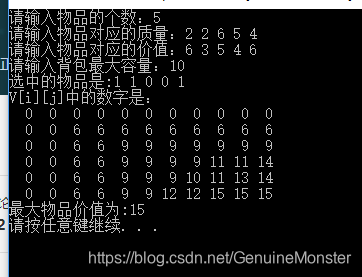
為了方便理解，我來多貼幾張圖，在這里就不做gif圖了，大家順著我的這個圖去理解。

函數種前兩個for循環程序執行之后：（藍色區域為最佳價值表區域）

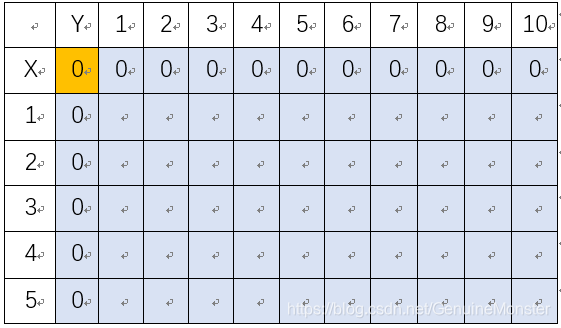
這個是只有物品1的時候：?

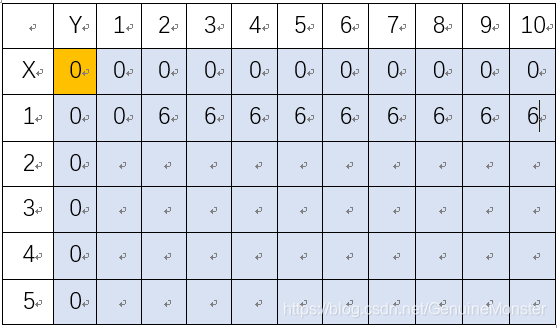
出現物品2：其中綠色的6就是一個在比較之后填入的價值，綠色的9是當前兩個物品的總和。

按照函數中的算法，一個一個模擬的把數字填寫進去，相信你就會理解這道題目了。