matlab ?filtic 函數應用 filter 解差分方程 dft 函數
一、 解差分方程
說明都在代碼注釋里面了
%這里要利用filtic函數 為濾波器的直接II型實現選擇初始條件
%求解查分方程 y(n) - 0.4y(n-1) - 0.45y(n-2) = 0.45x(n) +0.4x(n-1) - x(n-2)
%y(-1) = 0 y(-2) = 1 x(-1) = 1 x(-2) = 2
%x(n) = 0.8 ^u(n) 狀態方程H(z) = (0.45 + 0.4z^-1 - z^-2)/(1- 0.4z^-1-0.45z^-2)
% x 為濾波前序列 y 為輸出 序列
% 總結一下 首先把num 和den 寫出來
num = [ 0.45 0.4 -1];
den = [1 -0.4 -0.45]
% 其次把初始條件寫來
x0 = [1 2] ;
y0= [0 1];
N = 50 ;
n = [1 :N-1]';
x = 0.8.^n;
%生成初始條件
Zi = filtic(num, den , y0 , x0);
[y , Zf] = filter(num , den ,x, Zi);
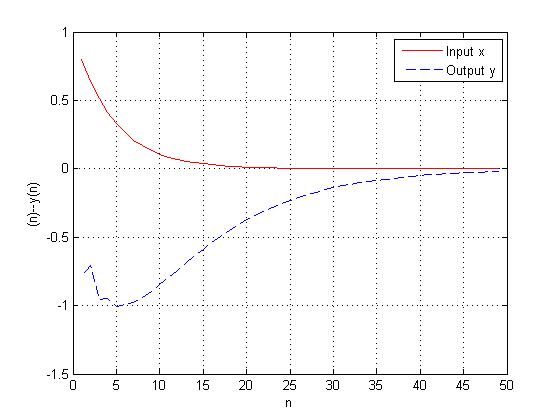
plot(n , x ,'R-', n, y, 'b--');
xlabel('n'); ylabel('(n)--y(n)');
legend('Input x' , 'Output y', 1);
grid;運行結果:
二、和上面類似簡單的解差分方程
%這里要借助filter 和filtic 解差分方程
%假設輸入信號為 x = 0.8.^n;
%求輸出序列
%差分方程y(n) = x(n) - 5x(n-1)+ 8x(n-3)
num = [1 -5 0 8];
N = 30 ;
n =[0: N-1] ;
x = 0.8.^n;
y = filter(num , 1, x);
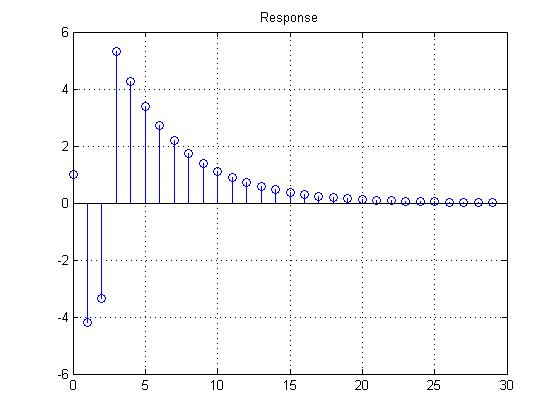
stem(n, y) ;
title('Response');
grid
運行結果:
三、dft 函數
%這里寫出一個dft函數
% Xk = DFT[xn] = 公式
% 總結一下dft 寫法首先確定xn N WN = exp(-j*2*pi/N)
%其次 確定nk = n'* k 再確定WNnk Xk = xn*WNnk
function [Xk] = dft(xn, N)
n = [0 :1 : N-1];
k = n ;
WN = exp(-j*2*pi/N);
nk = n'*k;
WNnk = WN.^nk;
Xk = xn*WNnk;
end
四、dft 應用
% x(n) = cos(0.48*pi*n) + cos(0.52*pi*n)
%繪制x(n) Xk(k) dft 變換
clf;
N = 100;
n = 0: N-1;
xn = cos(0.48*pi*n) + cos(0.52*pi*n);
Xk = dft(xn,N);
%幅度值 相位值
magXk = abs(Xk);
phaXk = angle(Xk);
% 原函數圖像
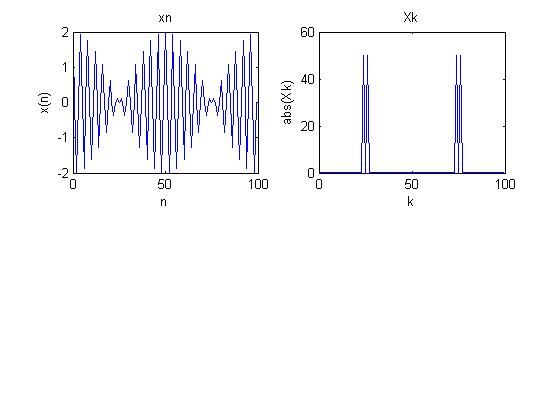
subplot(221);
plot(n,xn);
xlabel('n'); ylabel('x(n)');
title('xn');
%幅度頻率特性
subplot(222);
k = 0:length(magXk) - 1;
plot(k, magXk);
xlabel('k');
ylabel('abs(Xk)');
title('Xk');
運行結果:





)
--建表、添加、查詢)











)
