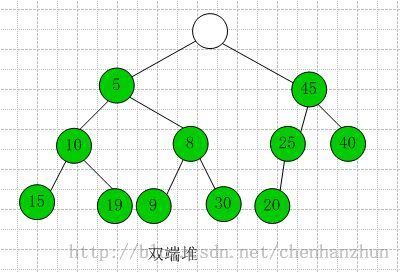
定義
雙端堆:是一棵完全二叉樹,該完全二叉樹要么為空,要么同時滿足下列性質:
(1)?根節點不包含元素;
(2)?左子樹是一個最小堆;
(3)?右子樹是一個最大堆;
(4)?如果右子樹不空,令i是左子樹中任意一節點,j是i在右子樹中的對應節點。如果i在右子樹中的對應節點不存在,則令j為i父節點在右子樹中的對應節點。對于節點i和j,節點i的關鍵字小于等于j的關鍵字。
雙端堆的插入操作
步驟
(1)若插入的新元素是在最小堆,將新插入節點與其在最大堆中對應節點相比較,如果大于對應節點,則將兩個節點元素互換,對最大堆執行max_insert操作;否則,只需對最小堆執行min_insert操作。
(2)若插入的新元素是在最大堆,將新插入節點與其在最小堆中對應節點相比較,如果小于對應節點,則將兩個節點元素互換,對最小堆執行min_insert操作;否則,只需對最大堆執行max_insert操作。
雙端堆的刪除操作
以下以刪除最小元素為例,刪除最大元素相似。
刪除最小元素基本思想:
首先,將從最小堆的根節點刪除的元素轉換為從最小堆的葉子節點中刪除元素的操作。這種轉換是通過在沿根節點到葉子節點的路徑上選擇關鍵字值較小的節點逐步上移來完成的。其結果是把初始時位于最小堆根節點處的空位移到一個葉子節點p。然后,用初始時位于雙端堆最后位置的元素temp插入到該葉子節點p。插入操作類似雙端堆的插入操作,只是插入操作僅在最小堆中進行,且其中max_paretner(i)的返回值j有改變。
程序
函數聲明:
#ifndef HEAP_H_INCLUDED
#define HEAP_H_INCLUDED
#include
#include
#include
#include
#define MAX_SIZE 10
int heap[MAX_SIZE];
void deap_insert(int *heap,int *n,int item);//雙端堆插入操作
int delete_deap_min(int *heap,int *n);//刪除雙端堆的最小元素
bool max_heap(int n);//判斷節點是否在最大堆中
int min_partner(int n);
int max_partner(int n);
void min_insert(int *heap,int n,int item);
void max_insert(int *heap,int n,int item);
void modified_deap_insert(int *heap,int i,int temp,int n);
int modified_max_partner(int i,int n);
#endif // HEAP_H_INCLUDED
函數定義:
#include"Heap.h"
/*雙端堆的插入操作*/
void deap_insert(int *heap,int *n,int item)
{
int i;
(*n)++;
if((*n)==MAX_SIZE)//滿堆
{
printf("The heap is full.\n");
exit(1);
}
if(2==(*n))//原來為空堆
heap[2]=item;
else
{
bool flag;
flag=max_heap(*n);//插入的節點是否在最大堆
switch(flag)
{
case true://節點在最大堆
i=min_partner(*n);//插入節點在最小堆所對應的節點
if(item
{
heap[*n]=heap[i];//交換元素
min_insert(heap,i,item);//把數據item插入到最小堆中
}
else
max_insert(heap,*n,item);//否則插入到最大堆中
break;
case false:
i=max_partner(*n);//插入節點在最大堆中對應的節點
if(item>heap[i])//比較最大堆節點和插入元素的大小
{
heap[*n]=heap[i];//交換元素
max_insert(heap,i,item);//插入到最大堆中
}
else
min_insert(heap,*n,item);//否則插入到最小堆
break;
}
}
}
/*刪除雙端堆的最小元素操作*/
int delete_deap_min(int *heap,int *n)
{
int i,j;
int temp;
int item;
if(*n<2)
{
fprintf(stderr,"The heap is empty.\n");
exit(1);
}
item=heap[2];//要刪除的元素
temp=heap[(*n)--];//最后元素賦給temp;
for(i=2;2*i<=*n;)
{//將從最小堆根節點刪除元素的操作
//轉換為從最小堆的葉子節點中刪除元素的操作
j=2*i;//j為i的葉子節點
if(j+1<=*n)
{
if(heap[j]>heap[j+1])
j++;//找出葉子節點中最小的關鍵字值節點
}
heap[i]=heap[j];//將葉子節點上移
i=j;//其結果是把初始時位于根節點處的空位移動到葉子節點i;
}
modified_deap_insert(heap,i,temp,*n);//用初始時位于雙端堆最后位置的節點元素插入到葉節點i;
//該插入操作與deap_insert()的插入操作基本類似;只是插入操作僅在最小堆中;且其中max_partner(i)
//的返回值j改變;
return item;
}
/*判斷節點n是否在最大堆中*/
bool max_heap(int n)
{
double a = log(n)/log(2);
double j = n + pow(2, (int)a-1);
double b = log(j)/log(2);
if((int)a == (int)b)
return false;
else
return true;
}
/*返回最大堆節點n對應最小堆的結點*/
int min_partner(int n)
{
double k = log(n)/log(2);
double a = pow(2, (int)k-1);
return n - (int)a;
}
/*返回最小堆節點n對應最大堆的結點*/
int max_partner(int n)
{
double k = log(n)/log(2);
double a = pow(2, (int)k-1);
return (n + (int)a)/2;
}
/*最小堆的插入操作*/
void min_insert(int *heap,int n,int item)
{
int i,parent;
i=n++;
parent=i/2;
while(parent>=1)
{
if(heap[parent]>item)
{
heap[i]=heap[parent];
i=parent;
parent/=2;
}
else break;
}
heap[i]=item;
}
/*最大堆的插入操作*/
void max_insert(int *heap,int n,int item)
{
int i,parent;
i=n++;
parent=i/2;
while(parent>1)
{
if(heap[parent]
{
heap[i]=heap[parent];
i=parent;
parent/=2;
}
else break;
}
heap[i]=item;
}
/*調整雙端堆*/
void modified_deap_insert(int *heap,int i,int temp,int n)
{
int j;
int item=temp;
i++;
if(i==MAX_SIZE)//滿堆
{
printf("The heap is full.\n");
exit(1);
}
if(2==i)//原來為空堆
heap[2]=item;
else
{
bool flag;
flag=max_heap(i);//插入的節點是否在最大堆
switch(flag)
{
case true://節點在最大堆
j=min_partner(i);//插入節點在最小堆所對應的節點
if(item
{
heap[i]=heap[j];//交換元素
min_insert(heap,j,item);//把數據item插入到最小堆中
}
else
max_insert(heap,i,item);//否則插入到最大堆中
break;
case false:
j=modified_max_partner(i,n);//插入節點在最大堆中對應的節點
if(item>heap[j])//比較最大堆節點和插入元素的大小
{
heap[i]=heap[j];//交換元素
max_insert(heap,j,item);//插入到最大堆中
}
else
min_insert(heap,i,item);//否則插入到最小堆
break;
}
}
}
int modified_max_partner(int i,int n)
{
double k = log(i)/log(2);
double a = pow(2, (int)k-1);
int j;
j=(i + (int)a);
if(j>n)
return j/2;
else return NULL;
}
程序測試:
#include"Heap.h"
int main()
{
int i,item;
int n=1;
for(i=2;i
{
scanf("%d",&item);
deap_insert(heap,&n,item);
}
for(i=2;i<=n;i++)
printf("%d ",heap[i]);
printf("\n");
item=delete_deap_min(heap,&n);
printf("The deleted data is:%d",item);
printf("\n");
for(i=2;i<=n;i++)
printf("%d ",heap[i]);
return 0;
}











...)



)
)

)
