在Matlab中,做短時傅里葉變換需要使用函數spectrogram,而在Matlab2019中,引入了一個新的函數stft,下面我們就來看下這兩個函數都如何使用。
短時傅里葉變換的基本原理就是將數據分段加窗,做fft,在分段時會有overlap,因此一個向量的短時傅里葉變換結果是一個矩陣。了解了這點,下面的函數及參數就更加容易理解了。
spectrogram
參數列表
先來看spectrogram函數,在更早期的版本中,這個函數的名字是specgram,幾種常用的用法如下:
spectrogram(x)
s = spectrogram(x)
s = spectrogram(x, window)
s = spectrogram(x, window, noverlap)
s = spectrogram(x, window, noverlap, nfft)
s = spectrogram(x, window, noverlap, nfft, fs)
[s, f, t] = spectrogram(x, window, noverlap, nfft, fs)
[s, f, t] = spectrogram(x, window, noverlap, f, fs)
[s, f, t, p] = spectrogram(x, window, noverlap, f, fs)
其中,
x表示輸入信號;window表示窗函數,如果window的值是一個整數,那么被分段的x的每一段的長度都等于window,并采用默認的Hamming窗;如果window是一個向量,那么被分段后每一段的長度都等于length(window),且輸入的向量即為所要加的窗函數;overlap表示兩段之間的重合點數,overlap的值必須要小于窗長,如果沒有指定overlap,默認是窗長的一半,即50%的overlap;nfft表示fft的點數,fft的點數跟窗長可以是不同的,當沒有指定該參數時,Matlab會取max(256, 2^(ceil(log2(length(window))))),即當窗長小于256時,fft的點數是256;當窗長大于256時,fft的點數取大于窗長的最小的2的整數次冪;fs表示采樣率,用來歸一化顯示使用;f表示顯示的頻譜范圍,f是一個向量,長度跟s的行數相同;- 當x是實信號且nfft為偶數時,s的行數為(nfft/2+1)
- 當x是實信號且nfft為奇數時,s的行數為(nfft+1)/2
- 當x是復信號時,s的行數為nfft
- 當在輸入的參數列表中指定f后,函數會在f指定的頻率處計算頻譜圖,返回的f跟輸入的f是相同的;
t表示顯示的時間范圍,是一個向量,長度跟s的列數相同;p表示功率譜密度,對于實信號,p是各段PSD的單邊周期估計;對于復信號,當指定F頻率向量時,P為雙邊PSD;如何計算PSD
Examples
首先,生成信號如下,4個點頻信號拼接起來:
clc;clear all;close all;
fs = 10e6;
n = 10000;
f1 = 10e3; f2 = 50e3; f3 = 80e3; f4 = 100e3;
t = (0:n-1)'/fs;
sig1 = cos(2*pi*f1*t);
sig2 = cos(2*pi*f2*t);
sig3 = cos(2*pi*f3*t);
sig4 = cos(2*pi*f4*t);sig = [sig1; sig2; sig3; sig4];
信號的時域波形如下:
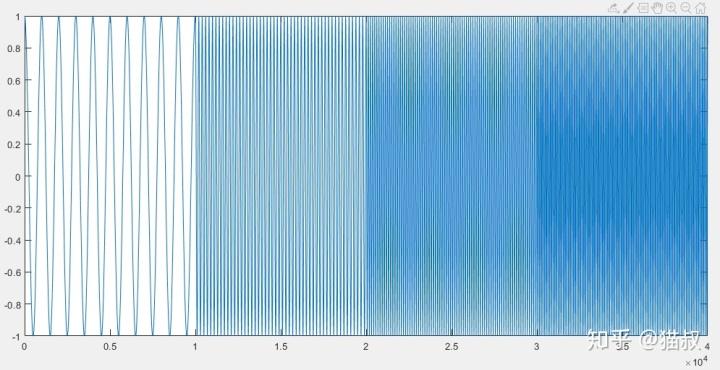
直接調用spectrogram(sig),可得如下結果,圖中默認橫軸是頻率,縱軸是時間
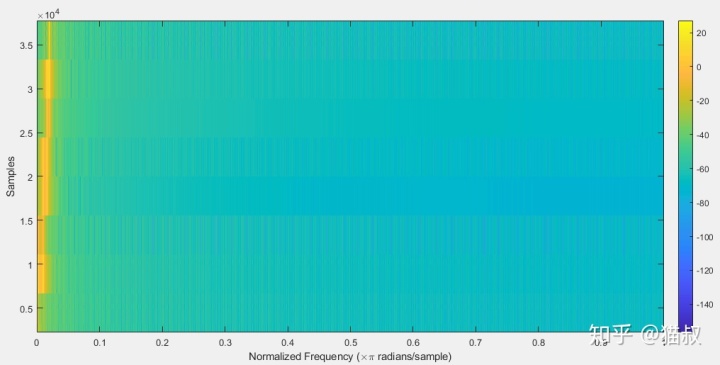
為了繪圖更靈活,我們不直接用spectrogram繪圖,而且求出s后,再對s單獨繪圖,這次我們指定window的大小為256
s = spectrogram(sig, 256);
t = linspace(0, 4*n/fs, size(s,1));
f = linspace(0, fs/2, size(s,2));
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;
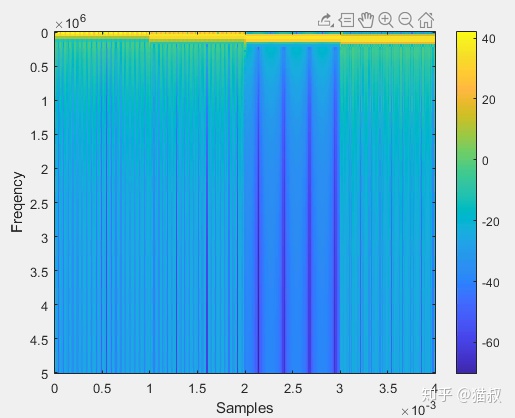
noverlap默認是50%,現在我們把它設為window的長度減1,即每次的步進為1
s = spectrogram(sig, 256, 255);
t = linspace(0, 4*n/fs, size(s,1));
f = linspace(0, fs/2, size(s,2));
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;
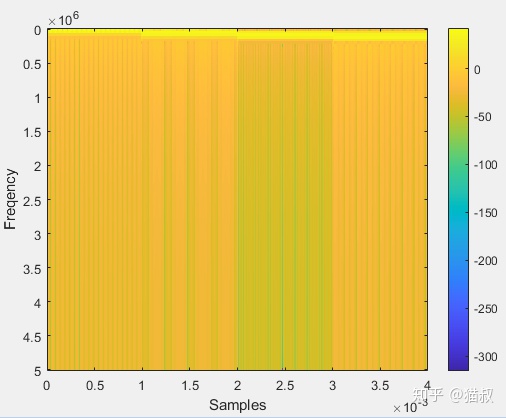
再加上nfft和fs參數,我們指定fft點數就是窗長
s = spectrogram(sig, 256, 128, 256, fs);
這個的圖形跟之前一樣,不再畫了
如果在返回值中,增加f和t,這樣我們下面就不用再重新定義f和t了
[s, f, t] = spectrogram(sig, 256, 128, 256, fs);
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;
從上面的圖中我們可以看出,我們的4個信號的頻率都比較小,而畫出來的圖顯示的頻譜范圍比較大,導致下面很大一部分信息我們其實都不需要。這時,我們就可以通過指定f的區間來計算頻譜。為了顯示效果更好,我們把其他參數也調一下
window = 2048;
noverlap = window/2;
f_len = window/2 + 1;
f = linspace(0, 150e3, f_len);
[s, f, t] = spectrogram(sig, window, noverlap , f, fs);
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
colorbar;
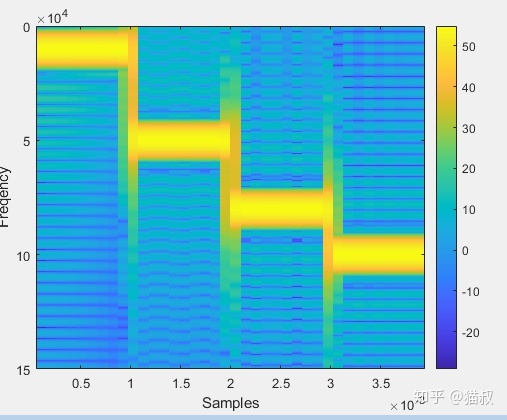
最后再把功率譜密度的返回值加上
[s, f, t, p] = spectrogram(sig, window, nfft, f, fs);
figure;
imagesc(t, f, p);xlabel('Samples'); ylabel('Freqency');
colorbar;
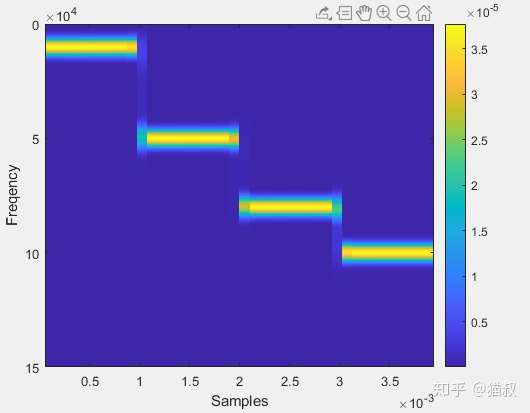
stft
這個函數在Matlab的解釋并不是很多,example也只寫了兩個,但用法比較簡單:
window = 2048;
noverlap = window/2;
nfft = window;
[s, f, t, p] = spectrogram(sig, window, noverlap, nfft, fs);
figure;
imagesc(t, f, 20*log10((abs(s))));xlabel('Samples'); ylabel('Freqency');
title('使用spectrogram畫出的短時傅里葉變換圖形');
colorbar;ss = stft(sig,fs,'Window',hamming(window),'OverlapLength',window/2,'FFTLength',nfft);
figure;
imagesc(t, f, 20*log10((abs(ss(1024:end,:)))));xlabel('Samples'); ylabel('Freqency');
title('使用stft畫出的短時傅里葉變換圖形');
colorbar;
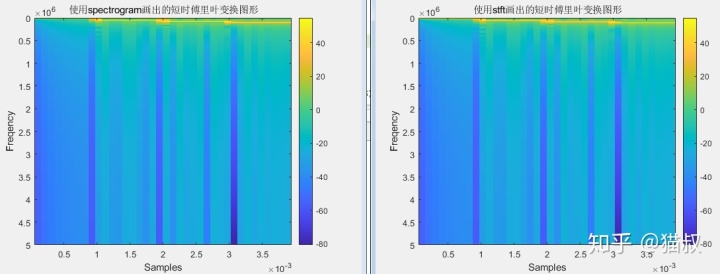
歡迎關注微信公眾號:Quant_Times
http://weixin.qq.com/r/Mi7t9T3EpWDarXmW93sg (二維碼自動識別)



![[唐詩]182宮中行樂詞(其一)-李白](http://pic.xiahunao.cn/[唐詩]182宮中行樂詞(其一)-李白)




)





瀏覽器兼容的JS寫法總結)
)



