標準定義如下:對于取定的方向θ 和距離 d, 在方向為θ的直線上, 一個像元灰度為 i, 另一個與其相距為 d
像元的灰度為 j 的點對出現的頻數即為灰度共生矩陣第(i, j)陣元的值。
怎樣理解呢?看起來好復雜呀 ?嗚嗚嗚
小白理解:灰度共生矩陣就是整幅圖像中,按照一定的平移方向,相距為d的兩個像素同時出現的聯合概率密度分布。
怎么樣?還是沒辦法深入理解
那就上圖吧
怎樣理解呢?
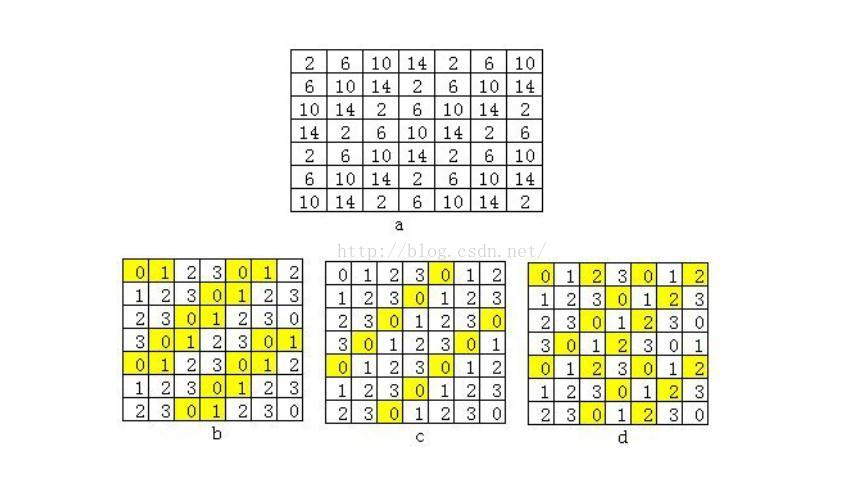
在上圖中,我定義的灰度級別是8,所以在右邊的灰度統計矩陣中就是8*8(拓展:如果灰度級別是k,則灰度統計矩陣就是k*k啦)。看圖很明白,左圖中定義的d肯定是1,平移方向當然是水平的啦。
看到這里應該算是有大概理解了吧。
那就開始正式上菜吧
取圖像(N×N)中任意一點 (x,y)及偏離它的另一點 (x+a,y+b),設該點對的灰度值為 (g1,g2)。令點(x,y) 在整個畫面上移動,則會得到各種 (g1,g2)值,設灰度值的級數為 k,則(g1,g2) 的組合共有 k 的平方種。對于整個畫面,統計出每一種 (g1,g2)值出現的次數,然后排列成一個方陣,再用(g1,g2) 出現的總次數將它們歸一化為出現的概率P(g1,g2) ,這樣的方陣稱為灰度共生矩陣。距離差分值(a,b) 取不同的數值組合,可以得到不同情況下的聯合概率矩陣。(a,b) 取值要根據紋理周期分布的特性來選擇,對于較細的紋理,選取(1,0)、(0,1)、(1,1)、(-1,1)等小的差分值。
當 a=1,b=0時,像素對是水平的,即0度掃描;當a=0,b=1 時,像素對是垂直的,即90度掃描;當 a=1,b=1時,像素對是右對角線的,即45度掃描;當 a=-1,b=1時,像素對是左對角線,即135度掃描。
綜上,兩個象素灰度級同時發生的概率,就將 (x,y)的空間坐標轉化為"灰度對" (g1,g2)的描述,形成了灰度共生矩陣。
補充一下:歸一化公式
---------------------?
作者:離原青草?
來源:CSDN?
原文:https://blog.csdn.net/yanghui0025/article/details/79703669?
版權聲明:本文為博主原創文章,轉載請附上博文鏈接!
-----------------------------------------------------------------------------------------------------------------------------------------------------
灰度共生矩陣(GLDM)的統計方法是20世紀70年代初由R.Haralick等人提出的,它是在假定圖像中各像素間的空間分布關系包含了圖像紋理信息的前提下,提出的具有廣泛性的紋理分析方法。
灰度共生矩陣被定義為從灰度為i的像素點出發,離開某個固定位置(相隔距離為d,方位為)的點上灰度值為的概率,即,所有估計的值可以表示成一個矩陣的形式,以此被稱為灰度共生矩陣。對于紋理變化緩慢的圖像,其灰度共生矩陣對角線上的數值較大;而對于紋理變化較快的圖像,其灰度共生矩陣對角線上的數值較小,對角線兩側的值較大。由于灰度共生矩陣的數據量較大,一般不直接作為區分紋理的特征,而是基于它構建的一些統計量作為紋理分類特征。Haralick曾提出了14種基于灰度共生矩陣計算出來的統計量:即:能量、熵、對比度、均勻性、相關性、方差、和平均、和方差、和熵、差方差、差平均、差熵、相關信息測度以及最大相關系數。
本文是借用一篇文章的例子講解灰度共生矩陣,用文字說明感覺說不清,自己之前用該方法做過實驗,還是會忘,所以干脆用例子的方式介紹,下一次再看也容易理解。
在圖像中任意一點(x,y)及偏離它的一點(x+a,y+b)(其中a,b為整數,認為定義)構成點對。設該點對的灰度值為(f1,f2),假設圖像的最大灰度級為L,則f1與f2的組合共有L*L種。對于整福圖像,統計每一種(f1,f2)值出現的次數,然后排列成一個方陣,再用(f1,f2)出現的總次數將它們歸一化為出現的概率P(f1,f2),由此產生的矩陣為灰度共生矩陣。
下圖為一個簡單的例子:
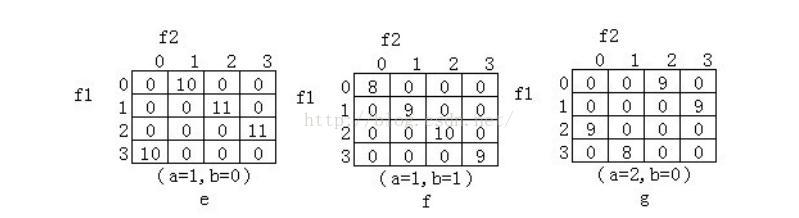
圖a為原圖像,最大灰度級為16。為表示方便,這里將灰度級數減小為4級,圖a變為圖b的形式。這樣(f1,f2)取值范圍便為[0,3]。取不同的間隔,將(f1,f2)各種組合出現的次數排列起來,就可得到圖e~g所示的灰度共生矩陣。
圖e表示圖b中(x,y)與偏離它的(x+1,y+0)構成點對時,(f1,f2)取值的情況(填充黃色部分為f1取0,f2取1時的情況,由圖b填充易知共10種)。同理,f,g分別表示圖c,d中(x,y)分別于點(x+1,y+1),(x+2,y+0)構成的點對(f1,f2)出現的情況(圖c填充黃色部分表示f1取0,f2取0時,對角線點對(0,0)出現的情況,共8種:圖d填充黃色部分表示f1取0,f2取2時水平點對(0,2)出現的情況,共9種)。例如,對于a=1,b=0,點對中(0,1)的組合共出現了10次。對比可以看出,(0,1),(1,2),(2,3)和(3,0)均有較高的出現頻數。圖b表明,圖像中存在明顯的左上右下方向的紋理。
距離(a,b)的取值不同,灰度共生矩陣中的值不同。a和b的取值要根據紋理周期分布的特征來選擇,對于較細的紋理,選取(1,0),(1,1),(2,0)等這樣的值是有必要的。a,b取值較小對應于變化緩慢的紋理圖像,其灰度共生矩陣對角線上的數值較大。紋理的變化越快,則對角線上的數值越小,而對角線兩側的值增大。
共生矩陣實際上是兩個像素點的聯合直方圖,對于圖像中細而規則的紋理,成對像素點的二維直方圖傾向于均勻分布;對于粗而規則的紋理,則傾向于最對角分布。
2.灰度共生矩陣特征量
2.1對比度
度量 矩陣的值是如何分布和圖像中局部變化的多少,反應了圖像的清晰度和紋理的溝紋深淺。紋理的溝紋越深,反差越大,效果越清晰;反之,對比值小,則溝紋淺,效果模糊。
2.2 能量
能量變換反映了圖像灰度分布均勻程度和紋理粗細度。若灰度共生矩陣的元素值相近,則能量較小,表示紋理細致;若其中一些值大,而其它值小,則能量值較大。能量值大表明一種較均一和規則變化的紋理模式。
2.3 熵
圖像包含信息量的隨機性度量。當共生矩陣中所有值均相等或者像素值表現出最大的隨機性時,熵最大;因此熵值表明了圖像灰度分布的復雜程度,熵值越大,圖像越復雜。
2.4 逆方差
逆方差反映了圖像紋理局部變化的大小,若圖像紋理的不同區域間較均勻,變化緩慢,逆方差會較大,反之較小。
2.5相關性
用來度量圖像的灰度級在行或列方向上的相似程度,因此值得大小反應了局部灰度相關性,值越大,相關性也越大。

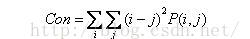

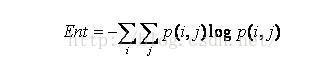



![[唐詩]182宮中行樂詞(其一)-李白](http://pic.xiahunao.cn/[唐詩]182宮中行樂詞(其一)-李白)




)





瀏覽器兼容的JS寫法總結)
)





)