必背定義、定理公式

1.三角形的面積＝底×高÷2

公式 S＝ a×h÷2

2.正方形的面積＝邊長×邊長

公式 S＝ a×a

3.長方形的面積＝長×寬

公式 S＝ a×b

4.平行四邊形的面積＝底×高

公式 S＝ a×h

5.梯形的面積＝(上底＋下底)×高÷2

公式 S＝(a＋b)h÷2

6.內角和：三角形的內角和＝180度

7.長方體的體積＝長×寬×高

公式：V＝a×b×h

8.正方體的體積＝棱長×棱長×棱長

公式：V＝a×a×a

9.圓的周長＝直徑×π

公式：L＝πd＝2πr

10.圓的面積＝半徑×半徑×π

公式：S＝πr2

11.圓柱的表(側)面積：圓柱的表(側)面積等于底面的周長乘高。

公式：S＝ch＝πdh＝2πrh

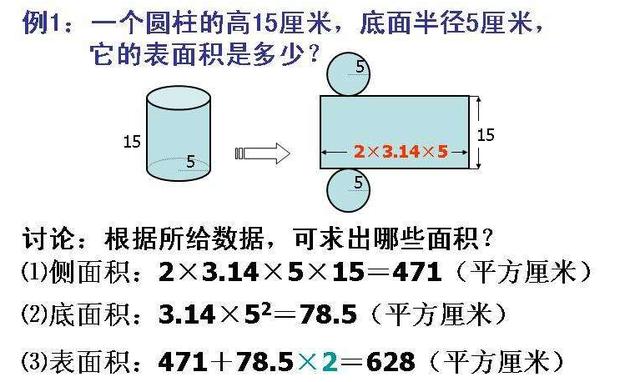
12.圓柱的表面積：圓柱的表面積等于底面的周長乘高再加上兩頭的圓的面積。

公式：S＝ch＋2s＝ch＋2πr2

13.圓柱的體積：圓柱的體積等于底面積乘高。

公式：V＝Sh

14.圓錐的體積＝1/3×底面積乘高。

公式：V＝1/3×Sh

15.分數的加、減法則：同分母的分數相加減，只把分子相加減，分母不變；異分母的分數相加減，先通分，然后再加減。

16.分數的乘法法則：用分子相乘的積作分子，用分母相乘的積作分母。

17.分數的除法法則：除以一個數(0除外)等于乘這個數的倒數。

算術方面

1.加法交換律：兩數相加，交換加數的位置，和不變。

2.加法結合律：三個數相加，先把前兩個數相加，或先把后兩個數相加，再同第三個數相加，和不變。

3.乘法交換律：兩數相乘，交換乘數的位置，積不變。

4.乘法結合律：三個數相乘，先把前兩個數相乘，或先把后兩個數相乘，再和第三個數相乘，它們的積不變。

5.乘法分配律：兩個數的和同一個數相乘，可以把兩個加數分別同這個數相乘，再把兩個積相加，結果不變。如(2＋4)×5＝2×5＋4×5。

6.除法的性質：在除法里，被除數和除數同時擴大(或縮小)相同的倍數，商不變。

7. 0除以任何不是0的數都得0。

8.簡便乘法：被乘數、乘數末尾有0的乘法，可以先把0前面的相乘，0不參加運算，有幾個0都落下，添在積的末尾。

9.什么叫等式？等號左邊的數值與等號右邊的數值相等的式子叫做等式。

10.等式的基本性質：等式兩邊同時乘(或除以)一個相同的數(0除外)，等式仍然成立。

11.什么叫方程？

答：含有未知數的等式叫方程。

12.分數：把單位“1”平均分成若干份，表示這樣的一份或幾份的數，叫做分數。

13.分數大小的比較：同分母的分數相比較，分子大的大，分子小的小；異分母的分數相比較，先通分然后再比較；若分子相同，分母大的反而小。

14.分數乘整數，用分數的分子和整數相乘的積作分子，分母不變。

15.真分數：分子比分母小的分數叫做真分數。

16.假分數：分子比分母大或者分子和分母相等的分數叫做假分數。假分數大于或等于1。

17.帶分數：把假分數寫成整數和真分數的形式，叫做帶分數。

18.分數的基本性質：分數的分子和分母同時乘或除以同一個數(0除外)，分數的大小不變。

19.一個數除以分數，等于這個數乘分數的倒數。

數量關系

1.單價×數量＝總價

2.單位產量×數量＝總產量

3.速度×時間＝路程

4.工作效率×時間＝工作總量

5.加數＋加數＝和

一個加數＝和－另一個加數

6.被減數－減數＝差

減數＝被減數－差

被減數＝減數＋差

7.因數×因數＝積

一個因數＝積÷另一個因數

8.被除數÷除數＝商

除數＝被除數÷商

被除數＝商×除數

9.有余數的除法：被除數＝商×除數＋余數

10.一個數連續用兩個數除，可以先把后兩個數相乘，再用它們的積去除這個數，結果不變。例：90÷5÷6＝90÷(5×6)。

11.

1千米＝1000米

1米＝10分米

1分米＝10厘米

1厘米＝10毫米

12.

1平方米＝100平方分米

1平方分米＝100平方厘米

1平方厘米＝100平方毫米

1公頃＝10000平方米

13.

1立方米＝1000立方分米

1立方分米＝1000立方厘米

1立方厘米＝1000立方毫米

1升＝1立方米

1毫升＝1立方厘米

14.

1噸＝1000千克

1千克＝ 1000克

15.比：兩個數相除就叫做兩個數的比。如2÷5或3:6或1/3。

16.比的前項和后項同時乘或除以一個相同的數(0除外)，比值不變。

17.比例：表示兩個比相等的式子叫做比例。如3:6＝9:18。

18.比例的基本性質：在比例里，兩外項之積等于兩內項之積。

19.解比例：求比例中的未知項，叫做解比例。如3:x＝9:18。

20.正比例：兩種相關聯的量，一種量變化，另一種量也隨著變化，如果這兩種量中相對應的比值(也就是商k)一定，這兩種量就叫做成正比例的量，它們的關系就叫做正比例關系。如：y/x＝k( k一定)或kx＝y。

21.反比例：兩種相關聯的量，一種量變化，另一種量也隨著變化，如果這兩種量中相對應的兩個數的積一定，這兩種量就叫做成反比例的量，它們的關系就叫做反比例關系。如：x×y＝k( k一定)或k / x＝y。

22.百分數：表示一個數是另一個數的百分之幾的數，叫做百分數。百分數也叫做百分率或百分比。

23.把小數化成百分數：只要把小數點向右移動兩位，同時在后面添上百分號。把百分數化成小數：只要把百分號去掉，同時把小數點向左移動兩位。

24.把分數化成百分數：通常先把分數化成小數(除不盡時，通常保留三位小數)，再把小數化成百分數。把百分數化成分數：先把百分數改寫成分數，能約分的要約成最簡分數。

25.最大公約數：幾個數都能被同一個數一次性整除，這個數就叫做這幾個數的最大公約數。(或幾個數公有的約數，叫做這幾個數的公約數。其中最大的一個，叫做最大公約數。)

26.互質數：公約數只有1的兩個數，叫做互質數。

27.最小公倍數：幾個數公有的倍數，叫做這幾個數的公倍數，其中最小的一個叫做這幾個數的最小公倍數。

28.通分：把異分母分數的分別化成和原來分數相等的同分母的分數，叫做通分。(通分用最小公倍數)

29.約分：把一個分數化成同它相等，但分子、分母都比較小的分數，叫做約分。(約分用最大公約數)

30.最簡分數：分子、分母是互質數的分數，叫做最簡分數。

31.偶數和奇數：能被2整除的數叫做偶數。不能被2整除的數叫做奇數。

32.質數(素數)：一個數，如果只有1和它本身兩個約數，這樣的數叫做質數(或素數)。

33.合數：一個數，如果除了1和它本身還有別的約數，這樣的數叫做合數。1不是質數，也不是合數。

34.利息＝本金×利率×時間(時間一般以年或月為單位，應與利率的單位相對應)

35.利率：利息與本金的比值叫做利率。一年的利息與本金的比值叫做年利率。一月的利息與本金的比值叫做月利率。

36.自然數：用來表示物體個數的整數，叫做自然數。0也是自然數。

37.循環小數：一個小數，從小數部分的某一位起，一個數字或幾個數字依次不斷地重復出現，這樣的小數叫做循環小數。如3.141414……。

38.不循環小數：一個小數，從小數部分起，沒有一個數字或幾個數字依次不斷地重復出現，這樣的小數叫做不循環小數。如3.141592654。

39.無限不循環小數：一個小數，從小數部分起到無限位數，沒有一個數字或幾個數字依次不斷地重復出現，這樣的小數叫做無限不循環小數。如3. 141592654……。