1 Random Forest和Gradient Tree Boosting參數詳解
在sklearn.ensemble庫中,我們可以找到Random Forest分類和回歸的實現:RandomForestClassifier和RandomForestRegression,Gradient Tree Boosting分類和回歸的實現:GradientBoostingClassifier和GradientBoostingRegression。有了這些模型后,立馬上手操練起來?少俠請留步!且聽我說一說,使用這些模型時常遇到的問題:
? ? ? 1、明明模型調教得很好了,可是效果離我的想象總有些偏差?——模型訓練的第一步就是要定好目標,往錯誤的方向走太多也是后退。
? ? ? 2、憑直覺調了某個參數,可是居然沒有任何作用,有時甚至起到反作用?——定好目標后,接下來就是要確定哪些參數是影響目標的,其對目標是正影響還是負影響,影響的大小。
? ? ? 3、感覺訓練結束遙遙無期,sklearn只是個在小數據上的玩具?——雖然sklearn并不是基于分布式計算環境而設計的,但我們還是可以通過某些策略提高訓練的效率。
? ? ? 4、模型開始訓練了,但是訓練到哪一步了呢?——飽暖思淫欲啊,目標,性能和效率都得了滿足后,我們有時還需要有別的追求,例如訓練過程的輸出,袋外得分計算等等。
通過總結這些常見的問題,我們可以把模型的參數分為4類:目標類、性能類、效率類和附加類。下表詳細地展示了4個模型參數的意義:
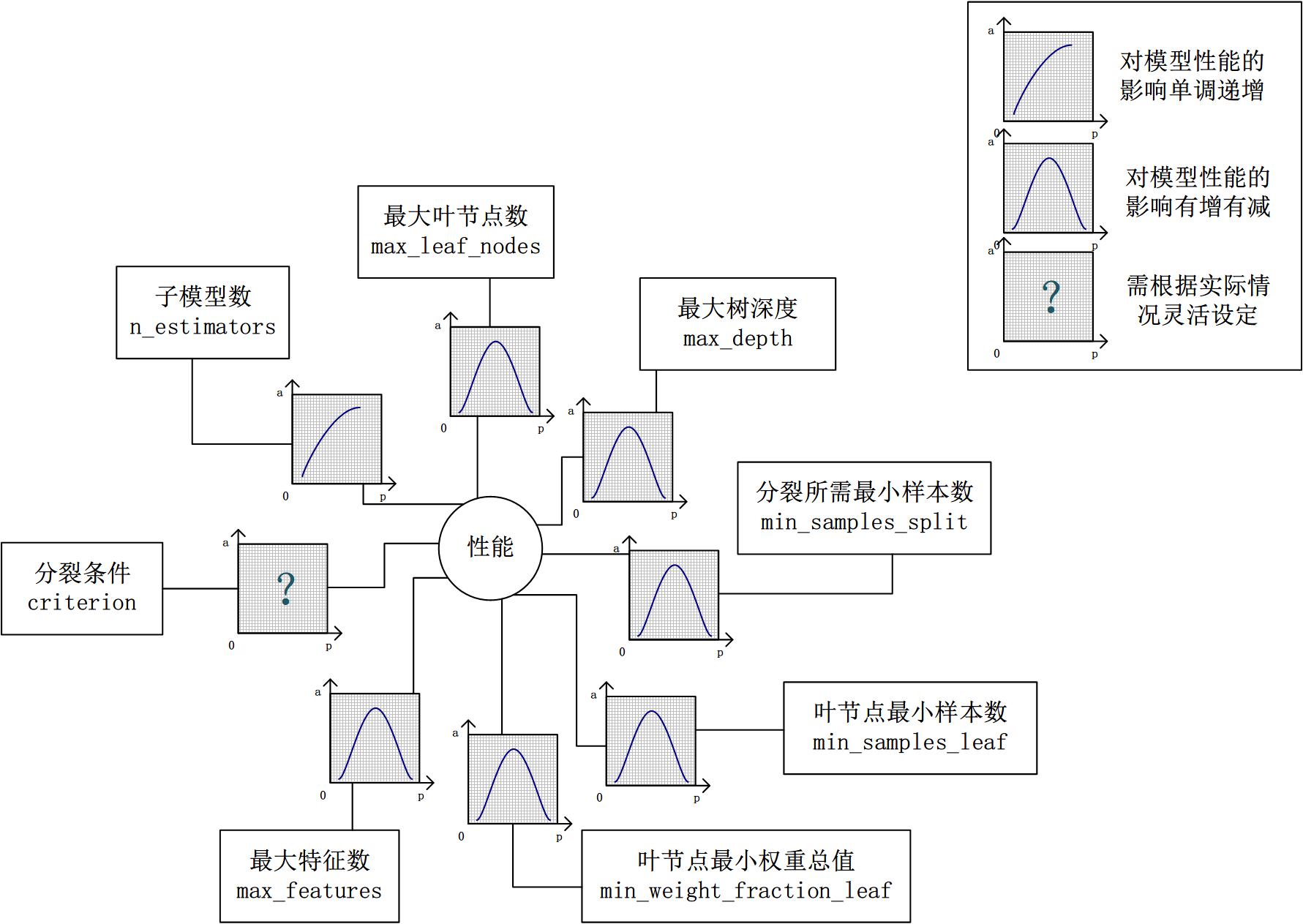
? ? ? 不難發現,基于bagging的Random Forest模型和基于boosting的Gradient Tree Boosting模型有不少共同的參數,然而某些參數的默認值又相差甚遠。在《使用sklearn進行集成學習——理論》一文中,我們對bagging和boosting兩種集成學習技術有了初步的了解。Random Forest的子模型都擁有較低的偏差,整體模型的訓練過程旨在降低方差,故其需要較少的子模型(n_estimators默認值為10)且子模型不為弱模型(max_depth的默認值為None),同時,降低子模型間的相關度可以起到減少整體模型的方差的效果(max_features的默認值為auto)。另一方面,Gradient Tree Boosting的子模型都擁有較低的方差,整體模型的訓練過程旨在降低偏差,故其需要較多的子模型(n_estimators默認值為100)且子模型為弱模型(max_depth的默認值為3),但是降低子模型間的相關度不能顯著減少整體模型的方差(max_features的默認值為None)。
2 如何調參?
聰明的讀者應當要發問了:”博主,就算你列出來每個參數的意義,然并卵啊!我還是不知道無從下手啊!”
參數分類的目的在于縮小調參的范圍,首先我們要明確訓練的目標,把目標類的參數定下來。接下來,我們需要根據數據集的大小,考慮是否采用一些提高訓練效率的策略,否則一次訓練就三天三夜,法國人孩子都生出來了。然后,我們終于進入到了重中之重的環節:調整那些影響整體模型性能的參數。
2.1 調參的目標:偏差和方差的協調
同樣在集成學習理論中,我們已討論過偏差和方差是怎樣影響著模型的性能——準確度。調參的目標就是為了達到整體模型的偏差和方差的大和諧!進一步,這些參數又可分為兩類:過程影響類及子模型影響類。在子模型不變的前提下,某些參數可以通過改變訓練的過程,從而影響模型的性能,諸如:“子模型數”(n_estimators)、“學習率”(learning_rate)等。另外,我們還可以通過改變子模型性能來影響整體模型的性能,諸如:“最大樹深度”(max_depth)、“分裂條件”(criterion)等。正由于bagging的訓練過程旨在降低方差,而boosting的訓練過程旨在降低偏差,過程影響類的參數能夠引起整體模型性能的大幅度變化。一般來說,在此前提下,我們繼續微調子模型影響類的參數,從而進一步提高模型的性能。
2.2 參數對整體模型性能的影響
假設模型是一個多元函數F,其輸出值為模型的準確度。我們可以固定其他參數,從而對某個參數對整體模型性能的影響進行分析:是正影響還是負影響,影響的單調性?
對Random Forest來說,增加“子模型數”(n_estimators)可以明顯降低整體模型的方差,且不會對子模型的偏差和方差有任何影響。模型的準確度會隨著“子模型數”的增加而提高。由于減少的是整體模型方差公式的第二項,故準確度的提高有一個上限。在不同的場景下,“分裂條件”(criterion)對模型的準確度的影響也不一樣,該參數需要在實際運用時靈活調整。調整“最大葉節點數”(max_leaf_nodes)以及“最大樹深度”(max_depth)之一,可以粗粒度地調整樹的結構:葉節點越多或者樹越深,意味著子模型的偏差越低,方差越高;同時,調整“分裂所需最小樣本數”(min_samples_split)、“葉節點最小樣本數”(min_samples_leaf)及“葉節點最小權重總值”(min_weight_fraction_leaf),可以更細粒度地調整樹的結構:分裂所需樣本數越少或者葉節點所需樣本越少,也意味著子模型越復雜。一般來說,我們總采用bootstrap對樣本進行子采樣來降低子模型之間的關聯度,從而降低整體模型的方差。適當地減少“分裂時考慮的最大特征數”(max_features),給子模型注入了另外的隨機性,同樣也達到了降低子模型之間關聯度的效果。但是一味地降低該參數也是不行的,因為分裂時可選特征變少,模型的偏差會越來越大。在下圖中,我們可以看到這些參數對Random Forest整體模型性能的影響:

2.3 一個樸實的方案:貪心的坐標下降法
到此為止,我們終于知道需要調整哪些參數,對于單個參數,我們也知道怎么調整才能提升性能。然而,表示模型的函數F并不是一元函數,這些參數需要共同調整才能得到全局最優解。也就是說,把這些參數丟給調參算法(諸如Grid Search)咯?對于小數據集,我們還能這么任性,但是參數組合爆炸,在大數據集上,或許我的子子孫孫能夠看到訓練結果吧。實際上網格搜索也不一定能得到全局最優解,而另一些研究者從解優化問題的角度嘗試解決調參問題。
坐標下降法是一類優化算法,其最大的優勢在于不用計算待優化的目標函數的梯度。我們最容易想到一種特別樸實的類似于坐標下降法的方法,與坐標下降法不同的是,其不是循環使用各個參數進行調整,而是貪心地選取了對整體模型性能影響最大的參數。參數對整體模型性能的影響力是動態變化的,故每一輪坐標選取的過程中,這種方法在對每個坐標的下降方向進行一次直線搜索(line search)。首先,找到那些能夠提升整體模型性能的參數,其次確保提升是單調或近似單調的。這意味著,我們篩選出來的參數是對整體模型性能有正影響的,且這種影響不是偶然性的,要知道,訓練過程的隨機性也會導致整體模型性能的細微區別,而這種區別是不具有單調性的。最后,在這些篩選出來的參數中,選取影響最大的參數進行調整即可。
無法對整體模型性能進行量化,也就談不上去比較參數影響整體模型性能的程度。是的,我們還沒有一個準確的方法來量化整體模型性能,只能通過交叉驗證來近似計算整體模型性能。然而交叉驗證也存在隨機性,假設我們以驗證集上的平均準確度作為整體模型的準確度,我們還得關心在各個驗證集上準確度的變異系數,如果變異系數過大,則平均值作為整體模型的準確度也是不合適的。










)


)






