在網上看到一篇GBDT介紹非常好的文章，GBDT大概是非常好用又非常好用的算法之一了吧(哈哈 兩個好的意思不一樣)

? ? ? ?

? ? ? ?GBDT(Gradient?Boosting?Decision?Tree)?又叫?MART（Multiple?Additive?Regression?Tree)，是一種迭代的決策樹算法，該算法由多棵決策樹組成，所有樹的結論累加起來做最終答案。它在被提出之初就和SVM一起被認為是泛化能力（generalization)較強的算法。近些年更因為被用于搜索排序的機器學習模型而引起大家關注。

?

? ? ? ?后記：發現GBDT除了我描述的殘差版本外還有另一種GBDT描述，兩者大概相同，但求解方法（Gradient應用）不同。其區別和另一版本的介紹鏈接見這里。由于另一版本介紹博客中亦有不少錯誤，建議大家還是先看本篇，再跳到另一版本描述，這個順序當能兩版本都看懂。

第1~4節：GBDT算法內部究竟是如何工作的？

第5節：它可以用于解決哪些問題？

第6節：它又是怎樣應用于搜索排序的呢？?

?

? ? ? ?在此先給出我比較推薦的兩篇英文文獻，喜歡英文原版的同學可直接閱讀：

【1】Boosting?Decision?Tree入門教程?http://www.schonlau.net/publication/05stata_boosting.pdf

【2】LambdaMART用于搜索排序入門教程?http://research.microsoft.com/pubs/132652/MSR-TR-2010-82.pdf

?

? ? ? ?GBDT主要由三個概念組成：Regression?Decistion?Tree（即DT)，Gradient?Boosting（即GB)，Shrinkage?(算法的一個重要演進分枝，目前大部分源碼都按該版本實現）。搞定這三個概念后就能明白GBDT是如何工作的，要繼續理解它如何用于搜索排序則需要額外理解RankNet概念，之后便功德圓滿。下文將逐個碎片介紹，最終把整張圖拼出來。

?

一、?DT：回歸樹?Regression?Decision?Tree

? ? ? ?提起決策樹（DT,?Decision?Tree)?絕大部分人首先想到的就是C4.5分類決策樹。但如果一開始就把GBDT中的樹想成分類樹，那就是一條歪路走到黑，一路各種坑，最終摔得都要咯血了還是一頭霧水說的就是LZ自己啊有木有。咳嗯，所以說千萬不要以為GBDT是很多棵分類樹。決策樹分為兩大類，回歸樹和分類樹。前者用于預測實數值，如明天的溫度、用戶的年齡、網頁的相關程度；后者用于分類標簽值，如晴天/陰天/霧/雨、用戶性別、網頁是否是垃圾頁面。這里要強調的是，前者的結果加減是有意義的，如10歲+5歲-3歲=12歲，后者則無意義，如男+男+女=到底是男是女？?GBDT的核心在于累加所有樹的結果作為最終結果，就像前面對年齡的累加（-3是加負3），而分類樹的結果顯然是沒辦法累加的，所以GBDT中的樹都是回歸樹，不是分類樹，這點對理解GBDT相當重要（盡管GBDT調整后也可用于分類但不代表GBDT的樹是分類樹）。那么回歸樹是如何工作的呢？

?

? ? ? ?下面我們以對人的性別判別/年齡預測為例來說明，每個instance都是一個我們已知性別/年齡的人，而feature則包括這個人上網的時長、上網的時段、網購所花的金額等。

?

? ? ? ?作為對比，先說分類樹，我們知道C4.5分類樹在每次分枝時，是窮舉每一個feature的每一個閾值，找到使得按照feature<=閾值，和feature>閾值分成的兩個分枝的熵最大的feature和閾值（熵最大的概念可理解成盡可能每個分枝的男女比例都遠離1:1），按照該標準分枝得到兩個新節點，用同樣方法繼續分枝直到所有人都被分入性別唯一的葉子節點，或達到預設的終止條件，若最終葉子節點中的性別不唯一，則以多數人的性別作為該葉子節點的性別。

?

? ? ? ?回歸樹總體流程也是類似，不過在每個節點（不一定是葉子節點）都會得一個預測值，以年齡為例，該預測值等于屬于這個節點的所有人年齡的平均值。分枝時窮舉每一個feature的每個閾值找最好的分割點，但衡量最好的標準不再是最大熵，而是最小化均方差--即（每個人的年齡-預測年齡）^2?的總和?/?N，或者說是每個人的預測誤差平方和?除以?N。這很好理解，被預測出錯的人數越多，錯的越離譜，均方差就越大，通過最小化均方差能夠找到最靠譜的分枝依據。分枝直到每個葉子節點上人的年齡都唯一（這太難了）或者達到預設的終止條件（如葉子個數上限），若最終葉子節點上人的年齡不唯一，則以該節點上所有人的平均年齡做為該葉子節點的預測年齡。若還不明白可以Google?"Regression?Tree"，或閱讀本文的第一篇論文中Regression?Tree部分。

?

二、?GB：梯度迭代?Gradient?Boosting

? ? ? ?好吧，我起了一個很大的標題，但事實上我并不想多講Gradient?Boosting的原理，因為不明白原理并無礙于理解GBDT中的Gradient?Boosting。喜歡打破砂鍋問到底的同學可以閱讀這篇英文wikihttp://en.wikipedia.org/wiki/Gradient_boosted_trees#Gradient_tree_boosting

?

? ? ? ?Boosting，迭代，即通過迭代多棵樹來共同決策。這怎么實現呢？難道是每棵樹獨立訓練一遍，比如A這個人，第一棵樹認為是10歲，第二棵樹認為是0歲，第三棵樹認為是20歲，我們就取平均值10歲做最終結論？--當然不是！且不說這是投票方法并不是GBDT，只要訓練集不變，獨立訓練三次的三棵樹必定完全相同，這樣做完全沒有意義。之前說過，GBDT是把所有樹的結論累加起來做最終結論的，所以可以想到每棵樹的結論并不是年齡本身，而是年齡的一個累加量。GBDT的核心就在于，每一棵樹學的是之前所有樹結論和的殘差，這個殘差就是一個加預測值后能得真實值的累加量。比如A的真實年齡是18歲，但第一棵樹的預測年齡是12歲，差了6歲，即殘差為6歲。那么在第二棵樹里我們把A的年齡設為6歲去學習，如果第二棵樹真的能把A分到6歲的葉子節點，那累加兩棵樹的結論就是A的真實年齡；如果第二棵樹的結論是5歲，則A仍然存在1歲的殘差，第三棵樹里A的年齡就變成1歲，繼續學。這就是Gradient?Boosting在GBDT中的意義，簡單吧。

?

三、?GBDT工作過程實例。

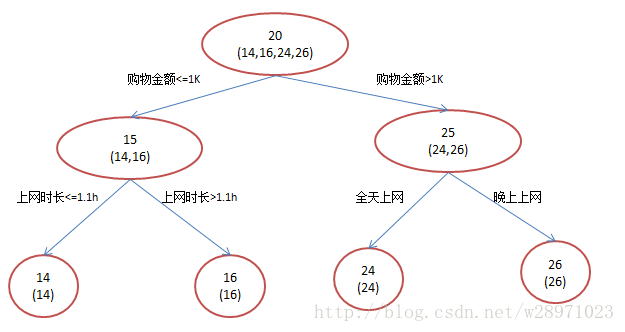
? ? ? ?還是年齡預測，簡單起見訓練集只有4個人，A,B,C,D，他們的年齡分別是14,16,24,26。其中A、B分別是高一和高三學生；C,D分別是應屆畢業生和工作兩年的員工。如果是用一棵傳統的回歸決策樹來訓練，會得到如下圖1所示結果：

?

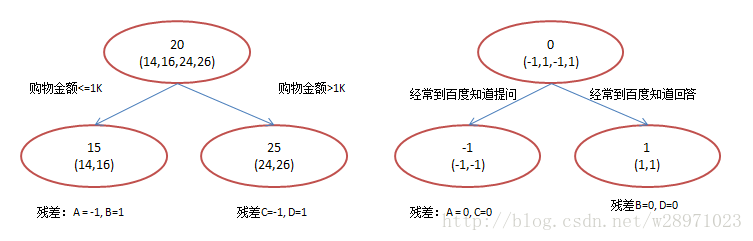
? ? ? ?現在我們使用GBDT來做這件事，由于數據太少，我們限定葉子節點做多有兩個，即每棵樹都只有一個分枝，并且限定只學兩棵樹。我們會得到如下圖2所示結果：

?

? ? ? ?在第一棵樹分枝和圖1一樣，由于A,B年齡較為相近，C,D年齡較為相近，他們被分為兩撥，每撥用平均年齡作為預測值。此時計算殘差（殘差的意思就是：?A的預測值?+?A的殘差?=?A的實際值），所以A的殘差就是16-15=1（注意，A的預測值是指前面所有樹累加的和，這里前面只有一棵樹所以直接是15，如果還有樹則需要都累加起來作為A的預測值）。進而得到A,B,C,D的殘差分別為-1,1，-1,1。然后我們拿殘差替代A,B,C,D的原值，到第二棵樹去學習，如果我們的預測值和它們的殘差相等，則只需把第二棵樹的結論累加到第一棵樹上就能得到真實年齡了。這里的數據顯然是我可以做的，第二棵樹只有兩個值1和-1，直接分成兩個節點。此時所有人的殘差都是0，即每個人都得到了真實的預測值。

?

? ? ? ?換句話說，現在A,B,C,D的預測值都和真實年齡一致了。Perfect!：

A:?14歲高一學生，購物較少，經常問學長問題；預測年齡A?=?15?–?1?=?14

B:?16歲高三學生；購物較少，經常被學弟問問題；預測年齡B?=?15?+?1?=?16

C:?24歲應屆畢業生；購物較多，經常問師兄問題；預測年齡C?=?25?–?1?=?24

D:?26歲工作兩年員工；購物較多，經常被師弟問問題；預測年齡D?=?25?+?1?=?26?

?

? ? ? ?那么哪里體現了Gradient呢？其實回到第一棵樹結束時想一想，無論此時的cost?function是什么，是均方差還是均差，只要它以誤差作為衡量標準，殘差向量(-1,?1,?-1,?1)都是它的全局最優方向，這就是Gradient。

?

? ? ? ?講到這里我們已經把GBDT最核心的概念、運算過程講完了！沒錯就是這么簡單。不過講到這里很容易發現三個問題：

?

1）既然圖1和圖2?最終效果相同，為何還需要GBDT呢？

? ? ? ?答案是過擬合。過擬合是指為了讓訓練集精度更高，學到了很多”僅在訓練集上成立的規律“，導致換一個數據集當前規律就不適用了。其實只要允許一棵樹的葉子節點足夠多，訓練集總是能訓練到100%準確率的（大不了最后一個葉子上只有一個instance)。在訓練精度和實際精度（或測試精度）之間，后者才是我們想要真正得到的。

? ? ? ?我們發現圖1為了達到100%精度使用了3個feature（上網時長、時段、網購金額），其中分枝“上網時長>1.1h”?很顯然已經過擬合了，這個數據集上A,B也許恰好A每天上網1.09h,?B上網1.05小時，但用上網時間是不是>1.1小時來判斷所有人的年齡很顯然是有悖常識的；

相對來說圖2的boosting雖然用了兩棵樹?，但其實只用了2個feature就搞定了，后一個feature是問答比例，顯然圖2的依據更靠譜。（當然，這里是LZ故意做的數據，所以才能靠譜得如此狗血。實際中靠譜不靠譜總是相對的）?Boosting的最大好處在于，每一步的殘差計算其實變相地增大了分錯instance的權重，而已經分對的instance則都趨向于0。這樣后面的樹就能越來越專注那些前面被分錯的instance。就像我們做互聯網，總是先解決60%用戶的需求湊合著，再解決35%用戶的需求，最后才關注那5%人的需求，這樣就能逐漸把產品做好，因為不同類型用戶需求可能完全不同，需要分別獨立分析。如果反過來做，或者剛上來就一定要做到盡善盡美，往往最終會竹籃打水一場空。

?

2）Gradient呢？不是“G”BDT么？

? ? ? ?到目前為止，我們的確沒有用到求導的Gradient。在當前版本GBDT描述中，的確沒有用到Gradient，該版本用殘差作為全局最優的絕對方向，并不需要Gradient求解.

?

3）這不是boosting吧？Adaboost可不是這么定義的。

? ? ? ?這是boosting，但不是Adaboost。GBDT不是Adaboost?Decistion?Tree。就像提到決策樹大家會想起C4.5，提到boost多數人也會想到Adaboost。Adaboost是另一種boost方法，它按分類對錯，分配不同的weight，計算cost?function時使用這些weight，從而讓“錯分的樣本權重越來越大，使它們更被重視”。Bootstrap也有類似思想，它在每一步迭代時不改變模型本身，也不計算殘差，而是從N個instance訓練集中按一定概率重新抽取N個instance出來（單個instance可以被重復sample），對著這N個新的instance再訓練一輪。由于數據集變了迭代模型訓練結果也不一樣，而一個instance被前面分錯的越厲害，它的概率就被設的越高，這樣就能同樣達到逐步關注被分錯的instance，逐步完善的效果。Adaboost的方法被實踐證明是一種很好的防止過擬合的方法，但至于為什么則至今沒從理論上被證明。GBDT也可以在使用殘差的同時引入Bootstrap?re-sampling，GBDT多數實現版本中也增加的這個選項，但是否一定使用則有不同看法。re-sampling一個缺點是它的隨機性，即同樣的數據集合訓練兩遍結果是不一樣的，也就是模型不可穩定復現，這對評估是很大挑戰，比如很難說一個模型變好是因為你選用了更好的feature，還是由于這次sample的隨機因素。

?

?

四、Shrinkage?

? ? ? ?Shrinkage（縮減）的思想認為，每次走一小步逐漸逼近結果的效果，要比每次邁一大步很快逼近結果的方式更容易避免過擬合。即它不完全信任每一個棵殘差樹，它認為每棵樹只學到了真理的一小部分，累加的時候只累加一小部分，通過多學幾棵樹彌補不足。用方程來看更清晰，即

沒用Shrinkage時：（yi表示第i棵樹上y的預測值，?y(1~i)表示前i棵樹y的綜合預測值）

y(i+1)?=?殘差(y1~yi)，?其中：?殘差(y1~yi)?=??y真實值?-?y(1?~?i)

y(1?~?i)?=?SUM(y1,?...,?yi)

Shrinkage不改變第一個方程，只把第二個方程改為：?

y(1?~?i)?=?y(1?~?i-1)?+?step?*?yi

?

? ? ? ?即Shrinkage仍然以殘差作為學習目標，但對于殘差學習出來的結果，只累加一小部分（step*殘差）逐步逼近目標，step一般都比較小，如0.01~0.001（注意該step非gradient的step），導致各個樹的殘差是漸變的而不是陡變的。直覺上這也很好理解，不像直接用殘差一步修復誤差，而是只修復一點點，其實就是把大步切成了很多小步。本質上，Shrinkage為每棵樹設置了一個weight，累加時要乘以這個weight，但和Gradient并沒有關系。這個weight就是step。就像Adaboost一樣，Shrinkage能減少過擬合發生也是經驗證明的，目前還沒有看到從理論的證明。

五、?GBDT的適用范圍

? ? ? ?該版本GBDT幾乎可用于所有回歸問題（線性/非線性），相對logistic?regression僅能用于線性回歸，GBDT的適用面非常廣。亦可用于二分類問題（設定閾值，大于閾值為正例，反之為負例）。

?

六、?搜索引擎排序應用?RankNet

? ? ? ?搜索排序關注各個doc的順序而不是絕對值，所以需要一個新的cost?function，而RankNet基本就是在定義這個cost?function，它可以兼容不同的算法（GBDT、神經網絡...）。

實際的搜索排序使用的是LambdaMART算法，必須指出的是由于這里要使用排序需要的cost?function，LambdaMART迭代用的并不是殘差。Lambda在這里充當替代殘差的計算方法，它使用了一種類似Gradient*步長模擬殘差的方法。這里的MART在求解方法上和之前說的殘差略有不同，其區別描述見這里。

? ? ? ?就像所有的機器學習一樣，搜索排序的學習也需要訓練集，這里一般是用人工標注實現，即對每一個(query,doc)?pair給定一個分值（如1,2,3,4）,分值越高表示越相關，越應該排到前面。然而這些絕對的分值本身意義不大，例如你很難說1分和2分文檔的相關程度差異是1分和3分文檔差距的一半。相關度本身就是一個很主觀的評判，標注人員無法做到這種定量標注，這種標準也無法制定。但標注人員很容易做到的是”AB都不錯，但文檔A比文檔B更相關，所以A是4分，B是3分“。RankNet就是基于此制定了一個學習誤差衡量方法，即cost?function。具體而言，RankNet對任意兩個文檔A,B，通過它們的人工標注分差，用sigmoid函數估計兩者順序和逆序的概率P1。然后同理用機器學習到的分差計算概率P2（sigmoid的好處在于它允許機器學習得到的分值是任意實數值，只要它們的分差和標準分的分差一致，P2就趨近于P1）。這時利用P1和P2求的兩者的交叉熵，該交叉熵就是cost?function。它越低說明機器學得的當前排序越趨近于標注排序。為了體現NDCG的作用（NDCG是搜索排序業界最常用的評判標準），RankNet還在cost?function中乘以了NDCG。

? ? ? ?好，現在我們有了cost?function，而且它是和各個文檔的當前分值yi相關的，那么雖然我們不知道它的全局最優方向，但可以求導求Gradient，Gradient即每個文檔得分的一個下降方向組成的N維向量，N為文檔個數（應該說是query-doc?pair個數）。這里僅僅是把”求殘差“的邏輯替換為”求梯度“，可以這樣想：梯度方向為每一步最優方向，累加的步數多了，總能走到局部最優點，若該點恰好為全局最優點，那和用殘差的效果是一樣的。這時套到之前講的邏輯，GDBT就已經可以上了。那么最終排序怎么產生呢？很簡單，每個樣本通過Shrinkage累加都會得到一個最終得分，直接按分數從大到小排序就可以了（因為機器學習產生的是實數域的預測分，極少會出現在人工標注中常見的兩文檔分數相等的情況，幾乎不同考慮同分文檔的排序方式）

? ? ? ?另外，如果feature個數太多，每一棵回歸樹都要耗費大量時間，這時每個分支時可以隨機抽一部分feature來遍歷求最優（ELF源碼實現方式）。