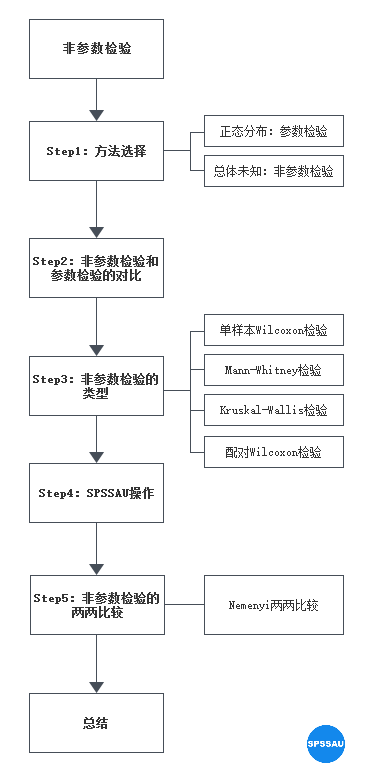
1. 何時使用非參數檢驗

或許你還沒有理解什么是參數檢驗、非參數檢驗，但一定曾在無意之中使用過它們。如我們常用的方差分析、T檢驗，都屬于參數檢驗。

參數檢驗，就是假定數據服從某種分布，通過樣本信息對總體參數進行檢驗。因而在分析前，先要檢驗數據是否符合該類型的分布，如果數據無法滿足檢驗假設的情況不符合分布情況，則可以考慮選擇使用非參數檢驗。

比如，使用方差分析時，需要在分析前對數據的正態性和方差齊性進行判斷，如果服從正態性、方差齊性，才可以使用方差分析。反之，如果沒有滿足這些假設條件，則考慮使用非參數檢驗。

2. 非參數檢驗和參數檢驗的對比

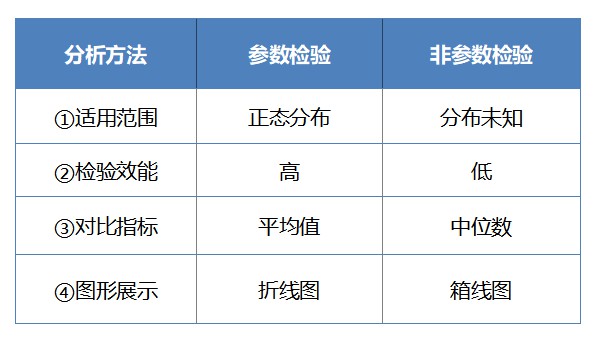
① 適用范圍：

非參數檢驗用作參數檢驗的替代方法，當數據不滿足正態性時，將使用非參數檢驗。因此，關鍵是要弄清楚是否具有正態分布。如果數據大致呈現"鐘型"分布，則可以使用參數檢驗。

② 檢驗效能：

如果數據滿足參數分布，應該優先選擇參數檢驗方法。愿因在于參數檢驗的檢驗效能要高于非參數檢驗。尤其是在樣本數較大的情況下，參數檢驗結果較為穩健，所以即使不服從正態分布，也會選擇參數檢驗。

③ 對比指標：

參數檢驗一般用平均值反映數據的集中趨勢；但由于數據不滿足正態分布，在非參數檢驗中如果再使用平均值描述顯然不太準確（比如常被吐槽的人均收入），此時中位數是更好的選擇。

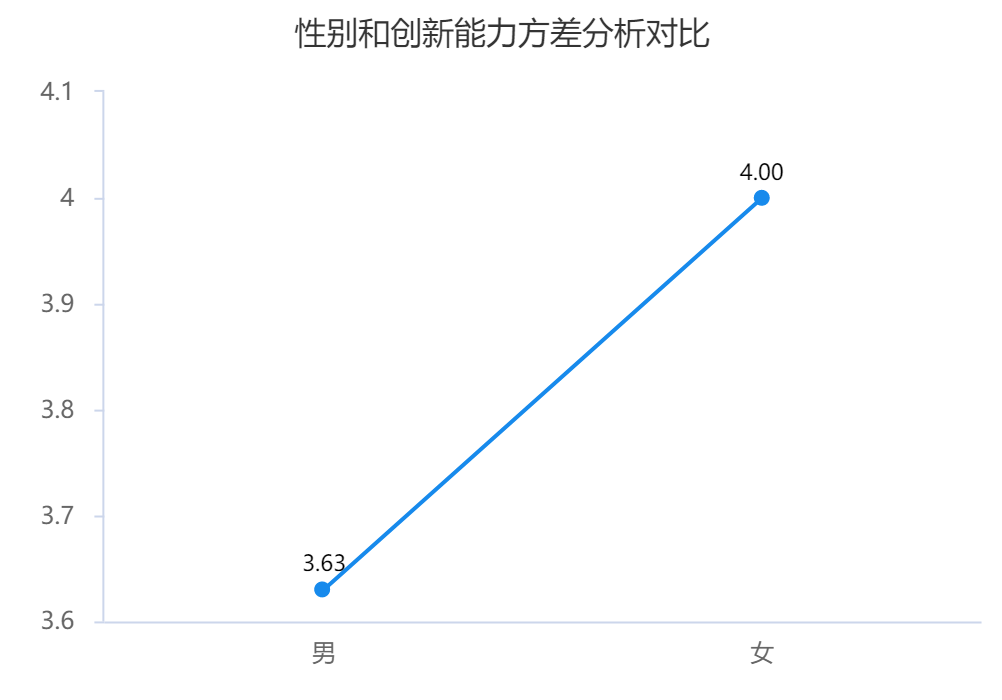
參數檢驗分析結果

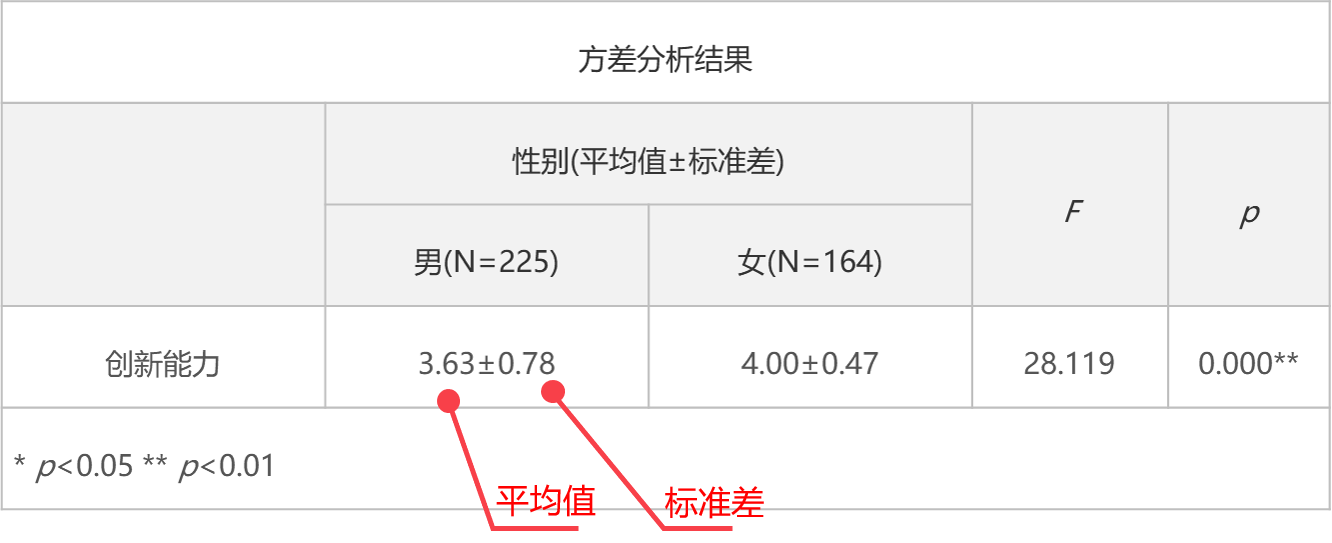
參數檢驗用平均值及標準差描述數據分布請況。

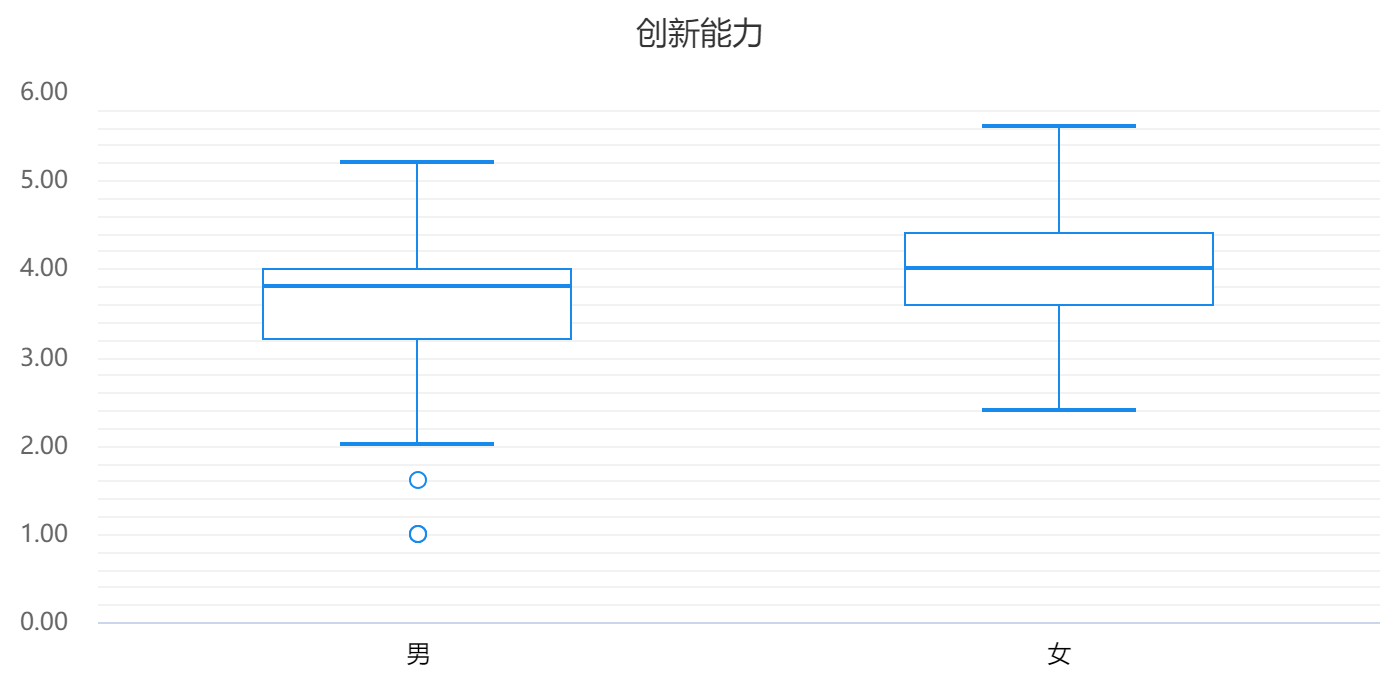
非參數檢驗分析結果

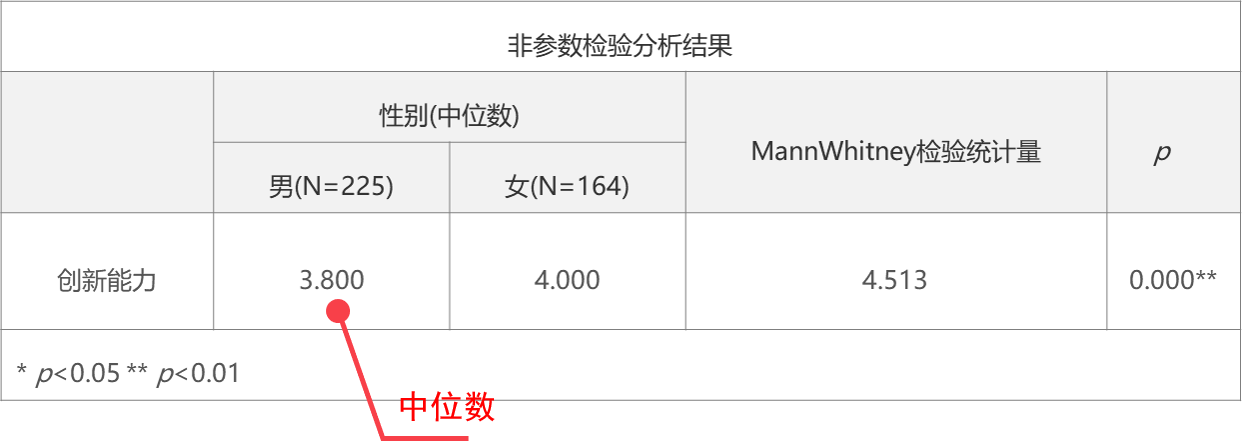
非參數檢驗結果中使用的是中位數描述差異。

④ 圖形展示：

除了使用以上指標進行分析，還可以通過圖形直觀展示數據情況。參數檢驗常用圖形有：折線圖、條形圖等，非參數檢驗可以使用箱線圖查看。

3. 非參數檢驗的類型

凡是在分析過程中不涉及總體分布參數的檢驗方法，都可以稱為“非參數檢驗”。因而，與參數檢驗一樣，非參數檢驗包括許多方法。以下是最常見的非參數檢驗及其對應的參數檢驗對應方法：

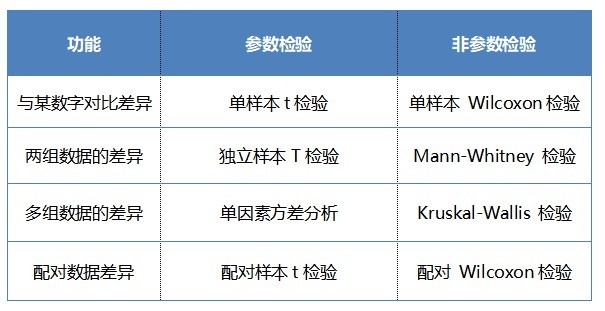
單樣本Wilcoxon檢驗

單樣本Wilcoxon檢驗是單樣本t檢驗的代替方法。該檢驗用于檢驗數據是否與某數字有明顯的區別，如對比調查對象整體態度與滿意程度之間的差異。

Mann-Whitney檢驗

Mann-Whitney檢驗是獨立樣本t檢驗的非參數版本。該檢驗主要處理包含等級數據的兩個獨立樣本，SPSSAU中稱為非參數檢驗。

Kruskal-Wallis檢驗

Kruskal-Wallis檢驗是單因素方差分析的非參數替代方法。Kruskal-Wallis檢驗用于比較兩個以上獨立組的等級數據。

在SPSSAU中，與Mann-Whitney檢驗統稱為“非參數檢驗”,分析時SPSSAU會根據自變量組別數自動選擇使用Kruskal-Wallis檢驗或Mann-Whitney檢驗。

配對Wilcoxon檢驗

Wilcoxon符號秩檢驗是配對樣本t檢驗的非參數對應方法。該檢驗將兩個相關樣本與等級數據進行比較。

4. SPSSAU操作

和參數檢驗一樣，進行非參數檢驗時應當遵循以下的步驟：

案例：分析不同性別學生，學習成績是否存在差異？

正態性檢驗

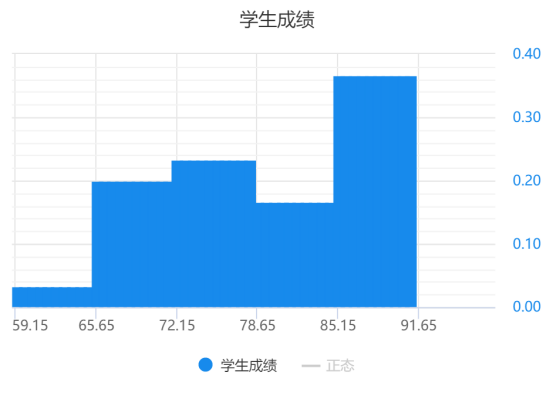
根據正態圖顯示，數據不服從正態分布，因而考慮使用非參數檢驗進行分析。

操作步驟

• 左側方法欄點擊【通用方法】→【非參數檢驗】；
• 將用于分組的自變量X放入【X(定類)】框；
• 因變量放入【Y（定量）】框；
• 點擊開始非參數檢驗分析。

結果分析

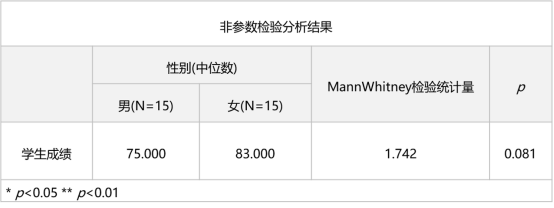
非參數檢驗分析步驟與參數檢驗步驟基本一致，建議參考SPSSAU輸出結果中的“分析建議”及“智能分析”即可。

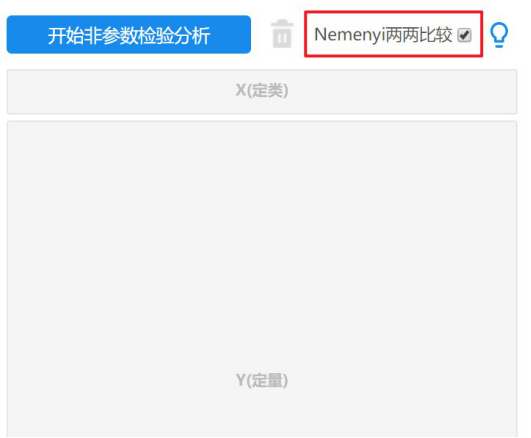
5. 兩兩比較

對應的方法是方差分析的事后檢驗，如果數據存在方差不齊或不服從正態性的情況，考慮使用非參數檢驗。

當結果呈現出顯著差異時，如果想進一步對比兩兩組別，可以在分析前勾選“Nemenyi兩兩比較”。

6. 總結

以上就是非參數檢驗的流程梳理，事實上在大部分研究中，如果可以使用參數檢驗，即使不滿足正態分布，也優先選擇參數檢驗，尤其是在樣本量較大的情況下。

更多內容登錄SPSSAU官網查看：

SPSSAU：從問卷設計到數據分析，近百篇教程合集真是太太太全面了！

SPSSAU：T檢驗分析思路完整總結，讓你條理清晰完成分析

SPSSAU：全流程總結方差分析，只看這篇就夠了

SPSSAU-在線SPSS分析軟件?www.spssau.com?100001000