二進制-高效位運算

數獨

數獨是介紹位運算的好例子，運用位運算和不運用效率差別還是挺大的。我們先看數獨需求:

1、當前數字所在行數字均含1-9，不重復

2、當前數字所在列數字均含1-9，不重復

3、當前數字所在宮（即3x3的大格）數字均含1-9，不重復（宮，如下圖每個粗線內是一個宮）

、

常規算法

若是我們采用常規方式的，每填寫一個數字，需要檢查當前行、列，宮中其他位置是否有重復數字，極端情況下需要循環27（3*9）次來進行檢查，我們看下常規算法下check

	int check(int sp) { // 檢查同行、列、九宮格有沒有相同的數字，若有傳回 1 int fg= 0 ; if(!fg) fg= check1(sp, startH[sp], addH) ; // 檢查同列有沒有相同的數字 if(!fg) fg= check1(sp, startV[sp], addV) ; // 檢查同行有沒有相同的數字 if(!fg) fg= check1(sp, startB[sp], addB) ; // 檢查同九宮格有沒有相同的數字 return(fg) ; } int check1(int sp, int start, int *addnum) { // 檢查指定的行、列、九宮格有沒有相同的數字，若有傳回 1 int fg= 0, i, sp1 ; //萬惡的for循環 for(i=0; i<9; i++) { sp1= start+ addnum[i] ; if(sp!=sp1 && sudoku[sp]==sudoku[sp1]) fg++ ; } return(fg) ; }

這個效率是否很嚇人，每次填寫一個就需要check27次，有木有check一次的算法？當然有了，采用位運算，一次搞定。來我們看下位運算的思路:

位運算

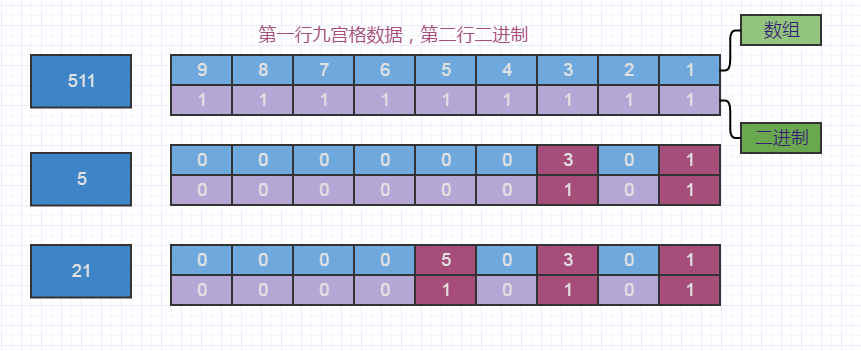
我們看上圖所示，單個行（或者列、宮）數據，都是有1-9共9個數字，我們統稱為九宮數字。若是我們采用二進制，以九宮數字充當二進制數據的位坐標,采用9位的二進制就可以與之一一對應，位上有數據，標識為1，無數據標識為0，如此一個正數就能解決一行九宮數據狀態，無需需存一個數組。

比如 看圖中深紅色部分，當前九宮數據中已經有1和3，那么二進制右起第一位和第三位標識為1，一個數字5就可以存下當前行（或者列、宮）數組狀態了,如若數字為511表明，所有的九宮數字都用完了，如圖第一行。

check一個數字是否已經被占用了，可以采取位運算來獲取二進制的右數第k位來查看是否是1，若是1，表明指定數字已經被占用了。我們看下具體check算法:

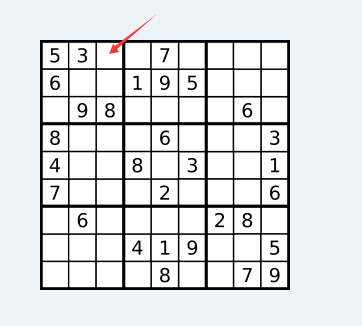
	// sp 是當前位置索引，indexV 行索引，indexH 列索引，indexB九宮格索引int check(int sp,int indexV,int indexH,int indexB) { // 檢查同行、列、九宮格沒有用到的數字，若已經用過返回 1 int status = statusV[indexV]|statusH[indexH]|statusB[indexB]; //9個數字都被用了 if (status>=STATUS_MAX_VALUE) { return 1; } int number=sudoku[sp]; //取右數第k位,若是1表明這個值已經存在了 return status>>(number-1)&1; } 

	// 行、列、宮二進制數據指定位置標記為1int markStatus(int indexV,int indexH,int indexB,int number){ if (number<1) { return 0; } //把右數第k(從1計數)位變成1 statusV[indexV]|=(1<<(number-1)); statusH[indexH]|=(1<<(number-1)); statusB[indexB]|=(1<<(number-1)); }

我們以以下圖例位置舉例，如何獲得當前位置可以填取的數字

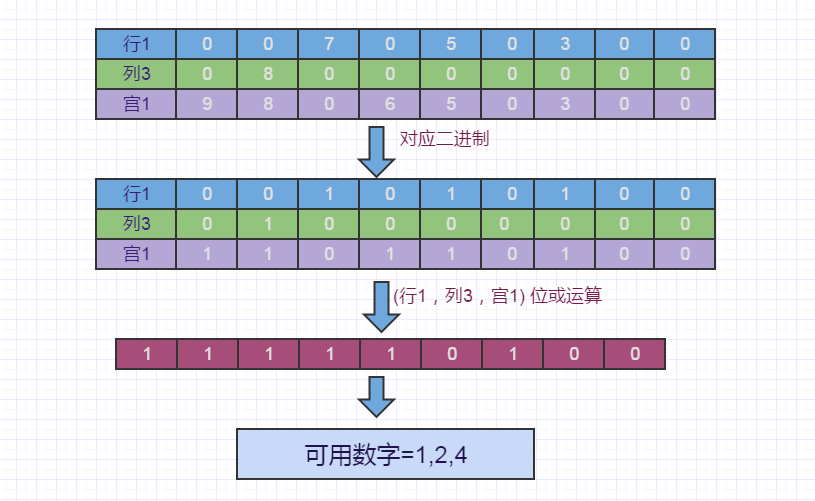
可以看到2個位運算就解決了檢查可用數字的操作了，而之前常規算法，需要用27次查找才可以獲取到。當然了這個算法還可以優化，比如采用啟發式DFS，搜索可用數字，速度更快，感興趣可點擊這里。

常規算法和位運算算法C語言代碼，我已經上傳碼云了，想了解的點擊下面鏈接，自行去查看去。（常規算法google的）

地址:?常規算法數獨，位運算版本數獨

?基礎

位操作符

符號	含義	規則
&?	與	兩個位都為1時，結果為1
|	或	有一個位為1時，結果為1
^	異或	0和1異或0都不變，異或1則取反
~	取反	0和1全部取反
<<	左移	位全部左移若干位，高位丟棄，低位補0
>>	算術右移	位全部右移若干位，，高位補k個最高有效位的值
>>	邏輯右移	位全部右移若干位，高位補0

注意:

1、位運算只可運用于整數，對于float和double不行。

2、另外邏輯右移符號各種語言不太同，比如java是>>>。

3、位操作符的運算優先級比較低，盡量使用括號來確保運算順序。比如1&i+1,會先執行i+1再執行&。

?

應用實例

很棒的應用實例，你可以mark一下，方便以后對照使用。

1、混合體

位運算實例

位運算	功能	示例
x >> 1	去掉最后一位	101101->10110
x << 1	在最后加一個0	101101->1011010
x << 1 | 1	在最后加一個1	101101->1011011
x | 1	把最后一位變成1	101100->101101
x & -2	把最后一位變成0	101101->101100
x ^ 1	最后一位取反	101101->101100
x | (1 << (k-1))	把右數第k位變成1	101001->101101,k=3
x & ~ (1 << (k-1))	把右數第k位變成0	101101->101001,k=3
x ^(1 <<(k-1))	右數第k位取反	101001->101101,k=3
?x & 7	取末三位	1101101->101
x & (1 << k-1)	取末k位	1101101->1101,k=5
x >> (k-1) & 1	取右數第k位	1101101->1,k=4
x | ((1 << k)-1)	把末k位變成1	101001->101111,k=4
x ^ (1 << k-1)	末k位取反	101001->100110,k=4
x & (x+1)	把右邊連續的1變成0	100101111->100100000
x | (x+1)	把右起第一個0變成1	100101111->100111111
x | (x-1)	把右邊連續的0變成1	11011000->11011111
(x ^ (x+1)) >> 1	取右邊連續的1	100101111->1111
x & -x	去掉右起第一個1的左邊	100101000->1000
x&0x7F	取末7位	100101000->101000
x& ~0x7F	是否小于127	001111111 &?~0x7F->0
x &?1	判斷奇偶	00000111&1->1

2、交換兩數

int swap(int a, int b) { if (a != b) { a ^= b; b ^= a; a ^= b; } } 

?

3、求絕對值

int abs(int a) { int i = a >> 31; return ((a ^ i) - i); } 

?

4、二分查找32位整數前導0個數

int nlz(unsigned x) { int n; if (x == 0) return(32); n = 1; if ((x >> 16) == 0) {n = n +16; x = x <<16;} if ((x >> 24) == 0) {n = n + 8; x = x << 8;} if ((x >> 28) == 0) {n = n + 4; x = x << 4;} if ((x >> 30) == 0) {n = n + 2; x = x << 2;} n = n - (x >> 31); return n; }

5、二進制逆序

int reverse_order(int n){ n = ((n & 0xAAAAAAAA) >> 1) | ((n & 0x55555555) << 1); n = ((n & 0xCCCCCCCC) >> 2) | ((n & 0x33333333) << 2); n = ((n & 0xF0F0F0F0) >> 4) | ((n & 0x0F0F0F0F) << 4); n = ((n & 0xFF00FF00) >> 8) | ((n & 0x00FF00FF) << 8); n = ((n & 0xFFFF0000) >> 16) | ((n & 0x0000FFFF) << 16); return n; }

6、?二進制中1的個數

 unsigned int BitCount_e(unsigned int value) { unsigned int count = 0; // 解釋下下面這句話代碼，這句話求得兩兩相加的結果，例如 11 01 00 10 // 11 01 00 10 = 01 01 00 00 + 10 00 00 10，即由奇數位和偶數位相加而成 // 記 value = 11 01 00 10，high_v = 01 01 00 00， low_v = 10 00 00 10 // 則 value = high_v + low_v，high_v 右移一位得 high_v_1， // 即 high_v_1 = high_v >> 1 = high_v / 2 // 此時 value 可以表示為 value = high_v_1 + high_v_1 + low_v， // 可見 我們需要 high_v + low_v 的和即等于 value - high_v_1 // 寫簡單點就是 value = value & 0x55555555 + (value >> 1) & 0x55555555; value = value - ((value >> 1) & 0x55555555); // 之后的就好理解了 value = (value & 0x33333333) + ((value >> 2) & 0x33333333); value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f); value = (value & 0x00ff00ff) + ((value >> 4) & 0x00ff00ff); value = (value & 0x0000ffff) + ((value >> 8) & 0x0000ffff); return value; // 另一種寫法，原理一樣，原因在最后一種解法中有提到 //value = (value & 0x55555555) + (value >> 1) & 0x55555555; //value = (value & 0x33333333) + ((value >> 2) & 0x33333333); //value = (value & 0x0f0f0f0f) + ((value >> 4) & 0x0f0f0f0f); //value = value + (value >> 8); //value = value + (value >> 16); //return (value & 0x0000003f); }

?