引言

首先說一下為什么要拿數組來模擬，最主要的原因是為了快，因為如果用stl庫里的容器的話，在算法競賽中，一般是不會給你開O2優化或者臭氧優化的，然后所以在一些時間卡的非常緊的情況下，還是推薦用數組來模擬會比較好，然后開始吧。

一、數組模擬鏈表

1.模板

const int N = 100010;//head為頭節點所在的下標,e[i]代表下標為i的值，ne[i]代表下標為i的下一個下標,idx代表當前可用的下標
int head, e[N], ne[N], idx;void init()
{head = -1;idx = 0;
}void add_to_head(int x)
{e[idx] = x;ne[idx] = head, head = idx++;
}void add(int k, int x)  //插到下標為k的后面
{e[idx] = x;ne[idx] = ne[k], ne[k] = idx++;
}void remove(int k)  //刪掉下標為k的后一個元素
{ne[k] = ne[ne[k]];
}

2.例題

實現一個單鏈表，鏈表初始為空，支持三種操作：向鏈表頭插入一個數；
刪除第 k 個插入的數后面的數；
在第 k 個插入的數后插入一個數。現在要對該鏈表進行 M 次操作，進行完所有操作后，從頭到尾輸出整個鏈表。注意:題目中第 k 個插入的數并不是指當前鏈表的第 k 個數。例如操作過程中一共插入了 n 個數，則按照插入的時間順序，這 n 個數依次為：第 1 個插入的數，第 2 個插入的數，…第 n 個插入的數。輸入格式
第一行包含整數 M，表示操作次數。接下來 M 行，每行包含一個操作命令，操作命令可能為以下幾種：H x，表示向鏈表頭插入一個數 x。D k，表示刪除第 k 個插入的數后面的數（當 k 為 0 時，表示刪除頭結點）。I k x，表示在第 k 個插入的數后面插入一個數 x（此操作中 k 均大于 0）。輸出格式
共一行，將整個鏈表從頭到尾輸出。數據范圍1≤M≤100000所有操作保證合法。輸入樣例：
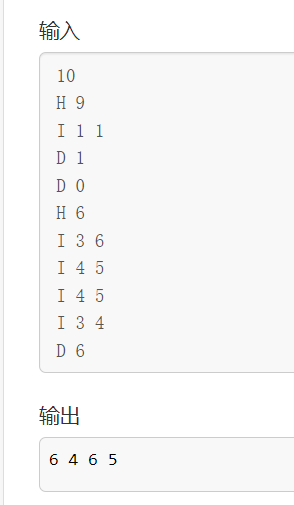
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6輸出樣例：
6 4 6 5

#include <iostream>using namespace std;const int N = 100010;int m;
int head, e[N], ne[N], idx;void init()
{head = -1;idx = 0;
}void add_to_head(int x)
{e[idx] = x;ne[idx] = head, head = idx++;
}void add(int k, int x)  //插到下標為k的后面
{e[idx] = x;ne[idx] = ne[k], ne[k] = idx++;
}void remove(int k)  //刪掉下標為k的后一個元素
{ne[k] = ne[ne[k]];
}int main()
{init();cin >> m;while(m--){int k, x;char op;cin >> op;if(op == 'H'){cin >> x;add_to_head(x);}else if(op == 'D'){cin >> k;if(!k) head = ne[head]; else remove(k-1);}else{cin >> k >> x;add(k-1, x);}}for(int i = head; i != -1; i = ne[i]) cout << e[i] << " ";cout << endl;return 0;
}

3.測試

可以看出是正確的

二、數組模擬雙鏈表

1.模板

const int N = 100010;int e[N], l[N], r[N], idx;void init()  //0代表左端點 1代表右端點
{r[0] = 1, l[1] = 0, idx = 2;  
}void insert(int k, int x)  //在結點k的右邊插入一個數x
{e[idx] = x;r[idx] = r[k], l[idx] = k;l[r[k]] = idx, r[k] = idx++;
}void remove(int k)  //刪除結點k
{r[l[k]] = r[k];l[r[k]] = l[k];
}

2.例題

實現一個雙鏈表，雙鏈表初始為空，支持 5 種操作：在最左側插入一個數；
在最右側插入一個數；
將第 k 個插入的數刪除；
在第 k 個插入的數左側插入一個數；
在第 k 個插入的數右側插入一個數現在要對該鏈表進行 M 次操作，進行完所有操作后，從左到右輸出整個鏈表。注意:題目中第 k 個插入的數并不是指當前鏈表的第 k 個數。例如操作過程中一共插入了 n 個數，則按照插入的時間順序，這 n 個數依次為：第 1 個插入的數，第 2 個插入的數，…第 n 個插入的數。輸入格式
第一行包含整數 M，表示操作次數。接下來 M 行，每行包含一個操作命令，操作命令可能為以下幾種：L x，表示在鏈表的最左端插入數 x。R x，表示在鏈表的最右端插入數 x。D k，表示將第 k 個插入的數刪除。IL k x，表示在第 k 個插入的數左側插入一個數。IR k x，表示在第 k 個插入的數右側插入一個數。輸出格式
共一行，將整個鏈表從左到右輸出。數據范圍1≤M≤100000所有操作保證合法。輸入樣例：
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2輸出樣例：
8 7 7 3 2 9

#include <iostream>using namespace std;const int N = 100010;int e[N], l[N], r[N], idx;void init()  //0代表左端點 1代表右端點
{r[0] = 1, l[1] = 0, idx = 2;  
}void insert(int k, int x)  //在結點k的右邊插入一個數x
{e[idx] = x;r[idx] = r[k], l[idx] = k;l[r[k]] = idx, r[k] = idx++;
}void remove(int k)  //刪除結點k
{r[l[k]] = r[k];l[r[k]] = l[k];
}int main()
{init();int m;cin >> m;while(m--){int k, x;string op;cin >> op;if(op == "L"){cin >> x;insert(0,x);}else if(op == "R"){cin >> x;insert(l[1],x);}else if(op == "D"){cin >> k;remove(k+1);  //因為k是從2開始的}else if(op == "IL"){cin >> k >> x;insert(l[k+1],x);}else{cin >> k >> x;insert(k+1,x);}}for(int i = r[0]; i != 1; i = r[i]) cout << e[i] << " ";return 0;
}

3.測試

可以看出是正確的

三、數組模擬棧

1.模板

const int N = 100010;int stk[N], tt;void push(int x)
{stk[++tt] = x;
}bool empty()
{return tt > 0 ? false : true;
}void pop()
{tt--;
}int top()
{return stk[tt]; 
}

2.例題

實現一個棧，棧初始為空，支持四種操作：push x – 向棧頂插入一個數 x；
pop – 從棧頂彈出一個數；
empty – 判斷棧是否為空；
query – 查詢棧頂元素。現在要對棧進行 M 個操作，其中的每個操作 3 和操作 4 都要輸出相應的結果。輸入格式
第一行包含整數 M，表示操作次數。接下來 M 行，每行包含一個操作命令，操作命令為 push x，pop，empty，query 中的一種。輸出格式
對于每個 empty 和 query 操作都要輸出一個查詢結果，每個結果占一行。其中，empty 操作的查詢結果為 YES 或 NO，query 操作的查詢結果為一個整數，表示棧頂元素的值。數據范圍
1≤M≤100000,1≤x≤109所有操作保證合法。輸入樣例：
10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty輸出樣例：
5
5
YES
4
NO

#include <iostream>using namespace std;const int N = 100010;int stk[N], tt;void push(int x)
{stk[++tt] = x;
}bool empty()
{return tt > 0 ? false : true;
}void pop()
{tt--;
}int top()
{return stk[tt]; 
}int main()
{int m;cin >> m;while(m--){string op;int x;cin >> op;if(op == "push"){cin >> x;push(x);}else if(op == "pop"){pop();}else if(op == "empty"){if(empty()) cout << "YES" << endl;else cout << "NO" << endl;}else{cout << top() << endl;}}return 0;
}

3.測試

四、數組模擬隊列

1.模板

const int N = 100010;int q[N], hh, tt = -1;void push(int x)
{q[++tt] = x;
}int front()
{return q[hh]; 
}void pop()
{hh++;
}bool empty()
{return hh <= tt ? false : true;
}

2.例題

實現一個隊列，隊列初始為空，支持四種操作：push x – 向隊尾插入一個數 x；
pop – 從隊頭彈出一個數；
empty – 判斷隊列是否為空；
query – 查詢隊頭元素。現在要對隊列進行 M 個操作，其中的每個操作 3 和操作 4 都要輸出相應的結果。輸入格式
第一行包含整數 M，表示操作次數。接下來 M 行，每行包含一個操作命令，操作命令為 push x，pop，empty，query 中的一種。輸出格式
對于每個 empty 和 query 操作都要輸出一個查詢結果，每個結果占一行。其中，empty 操作的查詢結果為 YES 或 NO，query 操作的查詢結果為一個整數，表示隊頭元素的值。數據范圍
1≤M≤100000,1≤x≤109,所有操作保證合法。輸入樣例：
10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6輸出樣例：
NO
6
YES
4

#include <iostream>using namespace std;const int N = 100010;int q[N], hh, tt = -1;void push(int x)
{q[++tt] = x;
}int front()
{return q[hh]; 
}void pop()
{hh++;
}bool empty()
{return hh <= tt ? false : true;
}int main()
{int m;cin >> m;while(m--){int x;string op;cin >> op;if(op == "push"){cin >> x;push(x);}else if(op == "pop"){pop();}else if(op == "empty"){if(empty()) cout << "YES" << endl;else cout << "NO" << endl;}else {cout << front() << endl;}}return 0;
}

3.測試

五、數組模擬單調棧

單調棧就是用來快速找當前下標左邊第一個小于該數的數

1.例題+模板

給定一個長度為 N 的整數數列，輸出每個數左邊第一個比它小的數，如果不存在則輸出 ?1。輸入格式
第一行包含整數 N，表示數列長度。第二行包含 N 個整數，表示整數數列。輸出格式
共一行，包含 N 個整數，其中第 i 個數表示第 i 個數的左邊第一個比它小的數，如果不存在則輸出 ?1。數據范圍
1≤N≤105，1≤數列中元素≤109輸入樣例：
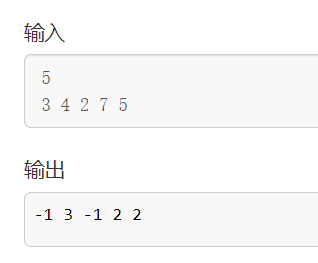
5
3 4 2 7 5輸出樣例：
-1 3 -1 2 2

#include <iostream>using namespace std;const int N = 100010;int stk[N], tt;int main()
{int n;cin >> n;while(n--){int x;cin >> x;while(tt && stk[tt] >= x) tt--;if(tt) printf("%d ", stk[tt]);else printf("-1 ");stk[++tt] = x;}return 0;
}

2.測試

六、數組模擬單調隊列

1.例題+模板

給定一個大小為 n≤106的數組。有一個大小為 k 的滑動窗口，它從數組的最左邊移動到最右邊。你只能在窗口中看到 k 個數字。每次滑動窗口向右移動一個位置。以下是一個例子：
該數組為 [1 3 -1 -3 5 3 6 7]，k 為 3。窗口位置	       最小值	最大值
[1 3 -1] -3 5 3 6 7	    -1	      3
1 [3 -1 -3] 5 3 6 7	    -3	      3
1 3 [-1 -3 5] 3 6 7		-3	      5
1 3 -1 [-3 5 3] 6 7		-3	      5
1 3 -1 -3 [5 3 6] 7	     3	      6
1 3 -1 -3 5 [3 6 7]	     3	      7
你的任務是確定滑動窗口位于每個位置時，窗口中的最大值和最小值。輸入格式
輸入包含兩行。第一行包含兩個整數 n 和 k，分別代表數組長度和滑動窗口的長度。第二行有 n 個整數，代表數組的具體數值。同行數據之間用空格隔開。輸出格式
輸出包含兩個。第一行輸出，從左至右，每個位置滑動窗口中的最小值。第二行輸出，從左至右，每個位置滑動窗口中的最大值。輸入樣例：
8 3
1 3 -1 -3 5 3 6 7輸出樣例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

#include <cstdio>
#include <iostream>using namespace std;const int N = 1000010;int a[N], q[N];
int n, k, hh, tt = -1;int main()
{scanf("%d%d", &n, &k);for(int i = 0; i < n; ++i) scanf("%d", &a[i]);for(int i = 0; i < n; ++i){//但因為這個每次只會進一個，所以用if就可以了if(hh <= tt && i - k + 1 > q[hh]) hh++;  //因為如果上一次滿了，然后上一次再入進去就會導致隊頭滑出窗口while(hh <= tt && a[q[tt]] >= a[i]) tt--;q[++tt] = i;if(i >= k - 1) printf("%d ", a[q[hh]]);}puts("");hh = 0, tt = -1;for(int i = 0; i < n; ++i){if(hh <= tt && i - k + 1 > q[hh]) hh++;  //因為如果上一次滿了，然后上一次再入進去就會導致隊頭滑出窗口while(hh <= tt && a[q[tt]] <= a[i]) tt--;q[++tt] = i;if(i >= k - 1) printf("%d ", a[q[hh]]);}puts("");return 0;
}

2.測試