目錄

簡介

搜索算法

二分法查找

排序算法

冒泡排序（Bubble Sort）

選擇排序（Selection Sort）

插入排序（Insert Sort）

快速排序（Quick Sort）

歸并排序（Merge Sort）

堆排序Heap Sort）

希爾排序（Shell?Sort）

計數排序（count_sort）

桶排序（Bucket Sort）

基數排序（Radix Sort）

總結

---

簡介

定義和特征

　　定義：算法（Algorithm）是指解題方案的準確而完整的描述，是一系列解決問題的清晰指令，算法代表著用系統的方法描述解決問題的策略機制。也就是說，能夠對一定規范的輸入，在有限時間內獲得所要求的輸出。如果一個算法有缺陷，或不適合于某個問題，執行這個算法將不會解決這個問題。不同的算法可能用不同的時間、空間或效率來完成同樣的任務。一個算法的優劣可以用空間復雜度與時間復雜度來衡量。

　　一個算法應該具有以下五個重要的特征：

• 有窮性：算法的有窮性是指算法必須能在執行有限個步驟之后終止；
• 確切性：算法的每一步驟必須有確切的定義；
• 輸入項：一個算法有0個或多個輸入，以刻畫運算對象的初始情況，所謂0個輸入是指算法本身定出了初始條件；
• 輸出項：一個算法有一個或多個輸出，以反映對輸入數據加工后的結果，沒有輸出的算法是毫無意義的；
• 可行性：算法中執行的任何計算步驟都是可以被分解為基本的可執行的操作步，即每個計算步都可以在有限時間內完成（也稱之為有效性）。
  ?

設計要求

算法設計的要求:?

• 確定性: 指的是算法至少應該有輸入,輸出和加工處理無歧義性，能正確反映問題的需求,能夠得到問題的正確答案。確定性大體分為四個層次:

1. 算法程序無語法錯誤;
2. 算法程序對于合法的輸入產生滿足要求的輸出;
3. 對于非法輸入能夠產生滿足規格的說明;
4. 算法程序對于故意刁難的測試輸入都有滿足要求的輸出結果。?

• 可讀性: 程序便于閱讀,理解交流。?
• 健壯性: 當輸入數據不合法時,算法也能作出相關處理，而不是產生異常,崩潰或者莫名其妙的結果。?
• 時間效率高和存儲量低。

算法效率的度量方法

　　事后統計方法：主要是通過設計好的測試程序和數據，利用計算機計時器對不同算法編制的程序的運行時間進行比較，從而確定算法效率的高低，但這種方法有很大缺陷，一般不予采納。

　　事前分析估算方法：在計算機程序編制前，依據統計方法對算法進行估算。

　　一個用高級語言編寫的程序在計算機上運行時所消耗的時間取決于以下因素：

1. 算法采用的策略，方法；（算法好壞的根本）
2. 編譯產生的代碼質量；（由軟件來支持）
3. 問題的輸入規模；（由數據決定）
4. 機器執行指令的速度。（看硬件的性能）

算法時間復雜度

　　定義：在進行算法分析時，語句總的執行次數T(n)是關于問題規模n的函數，進而分析T(n)隨n的變化情況并確定T(n)的數量級。算法的時間復雜度，也就是算法的時間量度，記作：T(n) = O(f(n))。它表示隨問題規模n的增大，算法執行時間的增長率和f(n)的增長率相同，稱作算法的漸近時間復雜度，簡稱為時間復雜度。其中f(n)是問題規定n的某個函數。

根據定義，求解算法的時間復雜度的具體步驟是：

1. 找出算法中的基本語句；算法中執行次數最多的那條語句就是基本語句，通常是最內層循環的循環體。
2. 計算基本語句的執行次數的數量級；只需計算基本語句執行次數的數量級，這就意味著只要保證基本語句執行次數的函數中的最高次冪正確即可，可以忽略所有低次冪和最高次冪的系數。這樣能夠簡化算法分析，并且使注意力集中在最重要的一點上：增長率。
3. 用大Ο記號表示算法的時間性能。將基本語句執行次數的數量級放入大Ο記號中。

如何推導大o階呢？下面是基本的推導方法：

1. 用常數1取代運行時間中的所有加法常數。
2. 在修改后的運行次數函數中，只保留最髙階項。
3. 如果最高階項存在且不是1,則去除與這個項相乘的常數。

簡單的說，就是保留求出次數的最高次冪，并且把系數去掉。 ?如T(n)=n2+n+1 =O(n2)

一些例子

######復雜度O(1)
print("this is wd")######復雜度O(n)
for i in range(n):print(i)######復雜度O(n2)
for i in range(n):for j in range(n):print(j)######復雜度O(n3)
for i in range(n):for j in range(n):for k in range(n):print('wd')######復雜度O(log2n)
while n > 1:print(n)n = n // 2

常見的復雜度按效率排序：O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(2nlogn)<O(n2)

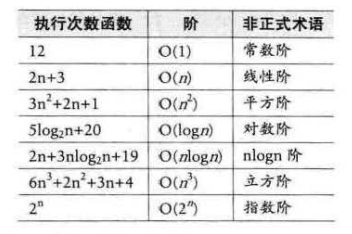
常見的時問復雜度如表所示。

空間復雜度?

空間復雜度(Space Complexity)是對一個算法在運行過程中臨時占用存儲空間大小的量度。一個算法在計算機存儲器上所占用的存儲空間，包括存儲算法本身所占用的存儲空間，算法的輸入輸出數據所占用的存儲空間和算法在運行過程中臨時占用的存儲空間這三個方面。算法的輸入輸出數據所占用的存儲空間是由要解決的問題決定的，是通過參數表由調用函數傳遞而來的，它不隨本算法的不同而改變。存儲算法本身所占用的存儲空間與算法書寫的長短成正比，要壓縮這方面的存儲空間，就必須編寫出較短的算法。算法在運行過程中臨時占用的存儲空間隨算法的不同而異，有的算法只需要占用少量的臨時工作單元，而且不隨問題規模的大小而改變，這種算法是節省存儲的算法；有的算法需要占用的臨時工作單元數與解決問題的規模n有關，它隨著n的增大而增大，當n較大時，將占用較多的存儲單元。

如當一個算法的空間復雜度為一個常量，即不隨被處理數據量n的大小而改變時，可表示為O(1)；當一個算法的空間復雜度與以2為底的n的對數成正比時，可表示為0(log2n)；當一個算法的空間復雜度與n成線性比例關系時，可表示為0(n).若形參為數組，則只需要為它分配一個存儲由實參傳送來的一個地址指針的空間，即一個機器字長空間；若形參為引用方式，則也只需要為其分配存儲一個地址的空間，用它來存儲對應實參變量的地址，以便由系統自動引用實參變量。?

最壞情況與平均情況

我們查找一個有n 個隨機數字數組中的某個數字，最好的情況是第一個數字就是，那么算法的時間復雜度為O(1)，但也有可能這個數字就在最后一個位置上待著，那么算法的時間復雜度就是O(n)，這是最壞的一種情況了。

最壞情況運行時間是一種保證，那就是運行時間將不會再壞了。 在應用中，這是一種最重要的需求， 通常， 除非特別指定， 我們提到的運行時間都是最壞情況的運行時間。

而平均運行時間也就是從概率的角度看， 這個數字在每一個位置的可能性是相同的，所以平均的查找時間為n/2次后發現這個目標元素。平均運行時間是所有情況中最有意義的，因為它是期望的運行時間。也就是說，我們運行一段程序代碼時，是希望看到平均運行時間的。可現實中，平均運行時間很難通過分析得到，一般都是通過運行一定數量的實驗數據后估算出來的。一般在沒有特殊說明的情況下，都是指最壞時間復雜度。

搜索算法

搜索是在一個數據集合中找到一個特定數據的算法，通常的答案是真的或假的。搜索的常見方法有二分查找、哈希查找等

二分法查找

二分查找又稱折半查找，優點是比較次數少，查找速度快，平均性能好。缺點是要求待查表為有序表。因此，折半查找方法適用于不經常變動而查找頻繁的有序列表。

二分查找的工作原理

• 首先，假設表中元素是按升序排列，將表中間位置記錄的關鍵字與查找關鍵字比較，如果兩者相等，則查找成功。
• 否則利用中間位置記錄將表分成前、后兩個子表，如果中間位置記錄的關鍵字大于查找關鍵字，則進一步查找前一子表，否則進一步查找后一子表。
• 重復以上過程，直到找到滿足條件的記錄，使查找成功，或直到子表不存在為止，此時查找不成功。

二分查找的實現

def binary(l, val):max = len(l)min = 0while min <=  max:mid = (max + min) // 2if l[mid] > val:max = mid - 1elif l[mid] < val:min = mid + 1elif l[mid] == val:print(mid)breakelse:print('no')def binary_rec(l, val, min, max):mid = (max + min) // 2if min > max:print('no')return 'no'if l[mid] == val:print(mid)return midelif l[mid] < val:return binary_rec(l, val, mid+1, max)elif l[mid] > val:return binary_rec(l, val, min, mid-1)

排序算法

冒泡排序（Bubble Sort）

• 時間復雜度：最優時間復雜度：O(n)，最壞時間復雜度：O(n2)。
• 優點：穩定，簡單
• 缺點：效率不很高，運行時間較長

原理如下：

1. 比較相鄰的元素，如果第一個比第二個大，就交換他們兩個；
2. 對每一對相鄰元素做同樣的工作，從開始第一對到結尾的最后一對。做完以后，最后的元素會是最大的數，這里可以理解為走了一趟；
3. 針對所有的元素重復以上的步驟，除了最后一個；
4. 持續每次對越來越少的元素重復上面的步驟，直到沒有任何一對數字需要比較，最后數列就是從大到小一次排列；

代碼實現

def bubble_sort(data):"""冒泡排序:param data: :return: """for i in range(len(data)-1):  # 趟數for j in range(len(data)-i-1):  # 遍歷數據，依次交換if data[j]>data[j+1]:  # 當較大數在前面data[j],data[j+1]=data[j+1],data[j] #交換兩個數的位置

優化版本：當某一趟走完以后發現并沒有進行數據交換，那么此時的數列已經排列好了，沒有必要在進行下去。例如：極端情況下，數列本來已經排序好的，我們只需要走一趟即可完成排序。

def bubble_sort(data):"""冒泡排序優化版:param data: :return: """for i in range(len(data)-1):  # 趟數exchange=False   # 交換標志for j in range(len(data)-i-1):  # 遍歷數據，依次交換if data[j]>data[j+1]:  # 當較大數在前面data[j],data[j+1]=data[j+1],data[j]  # 交換兩個數的位置exchange = True  # 改變標志if not exchange: # 如果某一趟沒有進行交換，代表排序完成breakreturn i  # 返回次數的趟數

選擇排序（Selection Sort）

• 時間復雜度：最優時間復雜度：O(n2)；最壞時間復雜度：O(n2)
• 穩定性：不穩定
• 優點：移動次數少
• 缺點：比較次數多

工作原理

1. 每一次從待排序的列表中選出一個元素，并將其與其他數依次比較，若列表中的某個數比選中的數小，則交換位置，把所有數比較完畢，則會選出最小的數，將其放在最左邊（這一過程稱為一趟）；
2. 重復以上步驟，直到全部待排序的數據元素排完；

實現

def select_sort(data):"""選擇排序:param data: 待排序的數據列表:return: """for i in range(len(data)-1):  #趟數min_index=i  # 記錄i趟開始最小的數的索引，我們從最左邊開始for j in range(i+1,len(data)): # 每一次趟需要循環的次數if data[j] < data[min_index]:  # 當數列中的某一個數比開始的數要小時候，更新最小值索引位置min_index=jdata[i],data[min_index]=data[min_index],data[i]  # 一趟走完，交換最小值的位置，第一趟最小

插入排序（Insert Sort）

• 時間復雜度：最優時間復雜度：O(n)；最壞時間復雜度：O(n2)
• 穩定性：穩定
• 優點：穩定，比較快
• 缺點：比較次數不確定，數據量越大，該算法越渣

工作原理如下：

1. 以從小到大排序為例，元素0為第一個元素，插入排序是從元素1開始，盡可能插到前面。
2. 插入時分插入位置和試探位置，元素i的初始插入位置為i，試探位置為i-1，在插入元素i時，依次與i-1,i-2······元素比較，如果被試探位置的元素比插入元素大，那么被試探元素后移一位，元素i插入位置前移1位，直到被試探元素小于插入元素或者插入元素位于第一位。
3. 重復上述步驟，最后完成排序

實現

def insert_sort(data):"""插入排序:param data: 待排序的數據列表:return: """for i in range(1, len(data)): # 無序區域數據tmp = data[i] # 第i次插入的基準數for j in range(i, -1, -1):if tmp < data[j - 1]:  # j為當前位置，試探j-1位置data[j] = data[j - 1]  #  移動當前位置else:  # 位置確定為jbreakdata[j] = tmp  # 將當前位置數還原

快速排序（Quick Sort）

• 時間復雜度：
• 最優時間復雜度：O(nlogn)遍歷每個數是O(n)，訪問每個數是O(logn)，最終是O(nlogn)可以轉換為求二叉樹深度的思想
• 最壞時間復雜度：O(n2)
• 穩定性：不穩定
• 優點：效率高，數據移動比較少，數據量越大，優勢越明顯
• 缺點：不穩定

快速排序（Quicksort），又稱劃分交換排序（partition-exchange sort）。通過一趟排序將要排序的數據分割成獨立的兩部分，其中一部分的所有數據都比另外一部分的所有數據都要小，然后再按此方法對這兩部分數據分別進行快速排序。整個排序過程可以遞歸進行，以此達到整個數據變成有序序列。

工作原理如下：

1. 從數列中隨機挑選出一個數作為基數；
2. 重新排列數列，使得比基數小的元素在左邊，比基數大元素在右邊，相等的元素放左邊或者右邊都可以，最后使得該基數在處于數列中間位置，這個稱為分區操作；
3. 遞歸上述操作，完成排序

實現

def quick_sort(data,left,right):"""快速排序:param data: 待排序的數據列表:param left: 基準數左邊元素的索引:param right: 基準數右邊元素的索引:return: """if left < right:mid = partition(data,left,right)  # 分區操作,mid代表基數所在的索引quick_sort(data,left,mid-1)   # 對基準數前面進行排序quick_sort(data,mid+1,right)  # 對基準數后面進行排序def partition(data,left,right):tmp=data[left]  # 隨機選擇的基準數,從最左邊開始選while left < right:while left < right and data[right] >= tmp:  # 右邊的數比基準數大right-=1  # 保留該數，然后索引指針往左移動data[left]=data[right]   # 否則此時右邊數比基數小，則將該數放到基準位置while left < right and data[left] <= tmp: # 右邊的數比基準數小left+=1  # 此時保持該數位置不動，索引指針往前移動data[right]=data[left]  # 否則此時左邊的數比基數大，則將該數放到右邊data[left] = tmp  # 最后將基準數量放回中間return left  # 返回基準數位置

歸并排序（Merge Sort）

• 最優時間復雜度：O(nlogn)最壞時間復雜度：O(nlogn)
• 穩定性：穩定
• 優點：穩定，數據量越大越優秀
• 缺點：需要額外空間

歸并排序（MergeSort）是采用分治法的一個非常典型的應用。歸并排序的思想就是先遞歸分解數組，再合并數組。

歸并排序是一種穩定的排序方法。和選擇排序一樣，歸并排序的性能不受輸入數據的影響，但表現比選擇排序好的多，因為始終都是O(nlogn）的時間復雜度。代價是需要額外的內存空間。

工作原理如下：

• 申請空間，使其大小為兩個已經排序序列之和，該空間用來存放合并后的序列；
• 設定兩個指針，最初位置分別為兩個已經排序序列的起始位置；
• 比較兩個指針所指向的元素，選擇相對小的元素放入到合并空間，并移動指針到下一位置；
• 重復步驟3直到某一指針達到序列尾；
• 將另一序列剩下的所有元素直接復制到合并序列尾

實現

def merge(data, low, mid, high):"""合并函數:param data: 數據列表:param low: 列表開頭位置:param mid: 分割中間位置:param high: 列表最后位置:return: """i = low  # 第一個指針j = mid + 1  # 第二個指針tmp = []  # 臨時存放的列表while i <= mid and j <= high:  # 分割的列表當兩邊都有數才進行if data[i] < data[j]:tmp.append(data[i])i += 1  # 低的指針往右移動else:tmp.append(data[j])  # 右邊大，存右邊的數j += 1  # 同時指針右移動while i <= mid:  # 左邊分割有剩下tmp.append(data[i])i += 1while j <= high:  # 右邊有剩下tmp.append(data[j])j += 1data[low:high + 1] = tmp  # 最后將tmp中的數寫入到原來的列表中def merge_sort(data, low, high):"""歸并排序:param data: 待排序的數據列表:param low: 數據列表開始位置:param high: 數據列表結束位置:return: """if low < high:  # 至少有兩個元素才進行mid = (low + high) // 2  # 分割merge_sort(data, low, mid)  # 遞歸分割上一部分merge_sort(data, mid + 1, high)  # 遞歸分割下一部分merge(data, low, mid, high)  # 合并

堆排序Heap Sort）

• 時間復雜度：最優時間復雜度：O(nlogn)，最壞時間復雜度：O(nlogn)
• 穩定性：不穩定

本質是一個完全二叉樹，如果根節點的值是所有節點的最小值稱為小根堆，如果根節點的值是所有節點的最大值，稱為大根堆。

原理：

1. 將待排序數據列表建立成堆結構(建立堆)；
2. 通過上浮(shift_up)或下沉(shift_down)等操作得到堆頂元素為最大元素（已大根堆為例）；
3. 去掉堆頂元素，將最后的一個元素放到堆頂，重新調整堆，再次使得堆頂元素為最大元素（相比第一次為第二大元素）；

• 重復3操作，直到堆為空，最后完成排序；??
• 

# -*- coding:utf8 -*-
import randomdef sift(li, low, high):# li表示樹, low表示樹根, high表示樹最后一個節點的位置tmp = li[low]i = lowj = 2 * i + 1 # 初識j指向空位的左孩子# i指向空位,j指向兩個孩子while j <= high: # 循環退出的第二種情況: j>high,說明空位i是葉子節點if j + 1 <= high and li[j] < li[j+1]: #如果右孩子存在并且比左孩子大,指向右孩子j += 1if li[j] > tmp:li[i] = li[j]i = jj = 2 * i + 1else: # 循環退出的第一種情況:j位置的值比tmp小,說明兩個孩子都比tmp小breakli[i] = tmpdef heap_sort(li):n = len(li)# 1. 構造堆for low in range(n//2-1, -1, -1):sift(li, low, n-1)# 2. 挨個出數for high in range(n-1, -1, -1):li[0], li[high] = li[high], li[0] # 退休 棋子sift(li, 0, high-1)import copyli = list(range(1000))
random.shuffle(li)
heap_sort(li)
print li

希爾排序（Shell?Sort）

• 最優時間復雜度：根據步長序列的不同而不同，最優是1.3，根據數學運算算出的gap
• 最壞時間復雜度：O(n2)
• 穩定性：不穩定
• 優點：平均時間短，數據移動少
• 缺點：不穩定

希爾排序（Shell Sort）是插入排序的一種，也稱縮小增量排序，是直接插入排序算法的一種更高效的改進版本。希爾排序是非穩定排序算法，是DL．Shell于1959年提出的。

工作原理如下：

1. 先取一個小于n的整數d1作為第一個增量，把文件的全部記錄分組。所有距離為d1的倍數的記錄放在同一個組中。
2. 先在各組內進行直接插入排序；
3. 取第二個增量d2<d1重復上述的分組和排序，直至所取的增量? =1(? <? …<d2<d1)，即所有記錄放在同一組中進行直接插入排序為止。

def shell_sort(data):"""希爾排序:param data:待排序的數據列表 :return: """d1 = len(data) // 2  # 設置分割大小為d1，while d1 > 0:for i in range(d1, len(data)):  # 在插入排序中 d1 為 1tmp = data[i]  # 當前分割元素位置j = i - d1  # 上一個分割元素位置while j >= 0 and tmp < data[j]:  # 上一個元素分割位置比當前分割位置要大，則需要調整位置data[j + d1] = data[j]  # 后移動當前分割元素位置j -= d1  # 往前移d1data[j + d1] = tmpd1 //= 2  # 繼續分割

計數排序（count_sort）

• 時間復雜度：最優時間復雜度：O(n)，最壞時間復雜度：O(n)
• 穩定性：穩定
• 優點：速度快
• 缺點：有局限性，范圍不能太大，只能是整數

計數排序不是基于比較的排序算法，其核心在于將輸入的數據值轉化為鍵存儲在額外開辟的數組空間中。 作為一種線性時間復雜度的排序，計數排序要求輸入的數據必須是有確定范圍的整數。

計數排序是一個穩定的排序算法。當輸入的元素是 n 個 0到 k 之間的整數時，時間復雜度是O(n+k)，空間復雜度也是O(n+k)，其排序速度快于任何比較排序算法。當k不是很大并且序列比較集中時，計數排序是一個很有效的排序算法。

算法描述

• 找出待排序的數組中最大和最小的元素；
• 統計數組中每個值為i的元素出現的次數，存入數組C的第i項；
• 對所有的計數累加（從C中的第一個元素開始，每一項和前一項相加）；
• 反向填充目標數組：將每個元素i放在新數組的第C(i)項，每放一個元素就將C(i)減去1。

def count_sort(li, max_num):count = [0 for i in range(max_num + 1)]  #設置計數序列并初始化為0for num in li:count[num] += 1i = 0for num,m in enumerate(count):for j in range(m):li[i] = numi += 1

桶排序（Bucket Sort）

• 時間復雜度：最優時間復雜度：O(n)，最壞時間復雜度：O(n)
• 穩定性：穩定
• 缺點：如果數據分布集中，如只分布在一個桶，效果不好。需要額外空間

桶排序是計數排序的升級版。它利用了函數的映射關系，高效與否的關鍵就在于這個映射函數的確定。桶排序 (Bucket sort)的工作的原理：假設輸入數據服從均勻分布，將數據分到有限數量的桶里，每個桶再分別排序（有可能再使用別的排序算法或是以遞歸方式繼續使用桶排序進行排）。

桶排序最好情況下使用線性時間O(n)，桶排序的時間復雜度，取決與對各個桶之間數據進行排序的時間復雜度，因為其它部分的時間復雜度都為O(n)。很顯然，桶劃分的越小，各個桶之間的數據越少，排序所用的時間也會越少。但相應的空間消耗就會增大。?

算法描述

• 設置一個定量的數組當作空桶；
• 遍歷輸入數據，并且把數據一個一個放到對應的桶里去；
• 對每個不是空的桶進行排序；
• 從不是空的桶里把排好序的數據拼接起來。?

def bucket_sort(data):buckets = [0] * ((max(data) - min(data)) + 1)  # 初始化桶元素為0for i in range(len(data)):buckets[data[i] - min(data)] += 1  # 遍歷數組a，在桶的相應位置累加值ret_data = []for i in range(len(buckets)):if buckets[i] != 0:ret_data += [i + min(data)] * buckets[i]print(ret_data)return ret_data

基數排序（Radix Sort）

• 時間復雜度：最優時間復雜度：O(n)，最壞時間復雜度：O(n)
• 穩定性：穩定
• 缺點：只能處理正整數。需要額外空間

基數排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次類推，直到最高位。有時候有些屬性是有優先級順序的，先按低優先級排序，再按高優先級排序。最后的次序就是高優先級高的在前，高優先級相同的低優先級高的在前。

基數排序基于分別排序，分別收集，所以是穩定的。但基數排序的性能比桶排序要略差，每一次關鍵字的桶分配都需要O(n)的時間復雜度，而且分配之后得到新的關鍵字序列又需要O(n)的時間復雜度。假如待排數據可以分為d個關鍵字，則基數排序的時間復雜度將是O(d*2n) ，當然d要遠遠小于n，因此基本上還是線性級別的。

基數排序的空間復雜度為O(n+k)，其中k為桶的數量。一般來說n>>k，因此額外空間需要大概n個左右。

算法描述

• 取得數組中的最大數，并取得位數；
• arr為原始數組，從最低位開始取每個位組成radix數組；
• 對radix進行計數排序（利用計數排序適用于小范圍數的特點）；

def radix_sort(li):max_num = max(li)i = 0while (10 ** i <= max_num):buckets = [[] for _ in range(10)]for val in li:digit = val // (10 ** i) % 10buckets[digit].append(val)li.clear()for bucket in buckets:for val in bucket:li.append(val)i += 1

總結

十大經典排序算法（動圖演示） - 一像素 - 博客園

Python算法基礎 - W-D - 博客園

python實現常見算法_流浮生的博客-CSDN博客_python實現算法