圖也是一種 非線性結構，是由多個頂點組成的關系集合組成的一種數據結構。圖可以分為兩種，無向圖和有向圖。

★圖的定義:

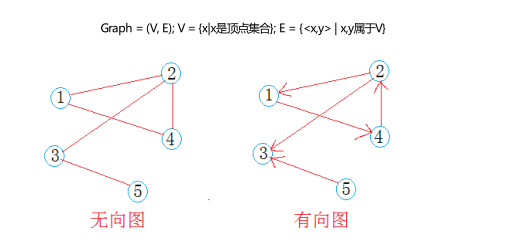
★典型問題：

利用圖能夠解決很多問題，這里有一個較為典型的問題，假如已知有n個人和m對好友關系(存于數字r)。如果兩個人是直接或者間接的好友(即就是好友的好友...)，則認為他們屬于一個朋友圈，請寫出程序求出這n個人里一共有多少個朋友圈。

例如：n = 5， m = 3， r = {{1,2},{2,3},{4,5}}, 表示有5個人，1和2是朋友，2和3也是朋友，4和5是朋友，則1,2,3屬于一個朋友圈，4、5屬于另一個朋友圈，結果為2個朋友圈。

★解題思路：

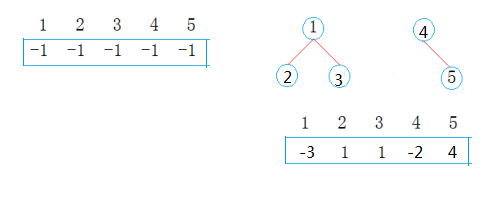
首先，先介紹一個概念：并查集。并查集就是將N個不同元素分成一組不想交的集合，開始時，每個元素就是一個集合，然后按規律將兩個集合進行合并。具體的做法如下：

設定一個有N個元素的數組，將每個元素對應的位置都置為-1，即就是先讓其沒有相交，然后根據題目中給出的朋友關系，將根節點元素對應的位置減1，將與根節點是好友的元素對應的位置更改為根節點元素，按照這樣的方式，將所有的關系都進行對應，最后數組中如果是負數，所對應的元素就是根節點。

★具體代碼：#pragma?once

#include?

//實現圖??——并查集

/*

主要功能：給定一個范圍，能夠確定朋友圈的個數

*/

class?UnionFindSet

{

public:

UnionFindSet(size_t?size)????//構造函數

:_n(size)

,?_set(new?int[size])

{

for?(int?i?=?0;?i?

{

_set[i]?=?-1;

}

}

void?Union(int?root1,?int?root2)????//結合兩個根節點

{

assert(_set[root1]?

assert(_set[root2]?

_set[root1]?+=?_set[root2];

_set[root2]?=?root1;

}

size_t?FindRoot(int?child)

{

if?(_set[child]?

{

return?child;

}

int?num?=?_set[child];

while?(num?>=?0)

{

num?=?_set[num];

}

return?num;

}

void?print()

{

int?root?=?0;

for?(int?i?=?0;?i?

{

if?(_set[i]?

{

root++;

}

}

cout?<

}

protected:

int*?_set;????//數組指針

size_t?_n;?????//給定范圍數據的個數

};

void?Test()

{

UnionFindSet?ht(10);

ht.Union(0,?6);

ht.Union(0,?7);

ht.Union(0,?8);

ht.Union(1,?4);

ht.Union(1,?9);

ht.Union(2,?3);

ht.Union(2,?5);

ht.print();

}