數值計算是指在數值分析領域中的算法。數值分析是專門研究和數字以及近似值相關的數據問題,數值計算在數值分析的研究中發揮了特別重要的作用。
多項式插值是計算函數近似值的一種方法。其中函數值僅在幾個點上已知。
該算法的基礎是建立級數小于等于n的一個插值多項式pn(z),其中n+1是已知函數值的點的個數。
多項式插值法
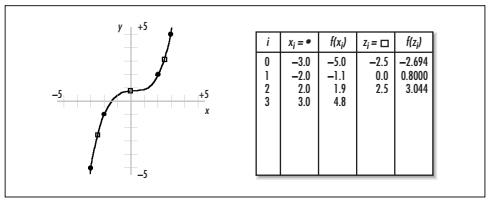
許多問題都可以按照函數的方式來描述。然而,通常這個函數是未知的,我們只能通過少量的已知點來推斷函數的大致模型。為了實現這個目的,在已知點之間做插值處理。如圖所示,關于函數f(x),已知的點為x0...x8,在圖中以黑色的圓點表示。通過插值法的幫助,我們能夠獲取函數在z0、z1、z2處的值,在圖中以白色小方塊表示。本節主要討論多項式插值法。

多項式插值法的根本點就是要建立一個特殊形式的多項式,稱為插值多項式。
為了深入理解插值多項式的意義,我們先來看看多項式的一些基本法則:
首先,多項式是具有如下形式的函數:
p(x) = a0 + a1x + a2x2 + ... + anxn
這里的a0,...,an是系數。當an為非零整數時,這種形式的多項式稱為n階多項式。這是多項式的指數形式,在數學問題中尤為常見。但是,在某些特定的環境中其他形式的多項式則更為簡便。比如,在有關多項式插值問題中,牛頓插值多項式就是一個很好的例子:
p(x) = a0 + a1 (x - c1) + a2 (x - c1)(x - c2) + ... + an(x - c1)(x - c2)...(x - cn)
這里a0,...,an是系數,而c0,...,cn是中值。注意到,當c0,...,cn全為0時,牛頓插值多項式就退化為前面定義的n階多項式。
構建插值多項式
下面我們來看看如何對函數f(x)構建一個插值多項式。
為了對函數f(x)進行插值,要構建一個階數小于等于n的多項式pn(z),而這又需要用到函數f(x)的n+1個已知點:x0,...,xn。這些已知點x0,...,xn就稱為插值點。通過插值多項式pn(z)可以計算出函數f(x)在x=z處的近似值。插值法需要滿足點z在[x0,xn]內。可以采用如下公式來構建插值多項式pn(z)。
pn(z) = f[x0] + f[x0,x1](z-x0) + f[x0,x1,x2](z-x0)(z-x1) + ... + f[x0,...,xn](z-x0)(z-x1)...(z-xn-1)
其中函數f(x)在點x0,...,xn處的值已知,而f[x0],...,f[x0,...,xn]則稱為差商。
差商可以通過點x0,...,xn以及函數f(x)在這些點處的值來計算得出。這就是牛頓插值多項式的計算公式。注意到該公式同牛頓插值多項式的相同點。差商的計算公式為:
f[xi,...,xj] = f(xi) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 如果i=j
f[xi,...,xj] = ( f[xi+1,...xj] - f[xi,...xj-1] ) / (xj - xi) 如果i < j
?通過這個公式不難看出,當i < j時,必須預先計算出其他的差商值。例如,要計算f[x0,x1,x2,x3],就需要先計算出f[x1,x2,x3]和f[x0,x1,x2]的值。幸運的是,可以通過一個差商表來幫助我們以一種系統的方式來計算差商值。如下圖。
差商表由多行組成。最頂行保存已知點x0,...,xn 的值。第二行保存f[x0],...,f[xn]的值。要計算出表中其他的差商值,從每個待求的差商值處畫一條對角線,使其回到f[xi]和f[xj](如下圖中差商f[x1,x2,x3]處的虛線)。要得到分母中的xi和xj,直接通過xi和xj求得。分子中的兩個差商就是前一階段計算出來的結果。
當完成了整個差商表的計算后,插值多項式的系數就是從第二行開始,每行最左邊的那一項。

計算插值多項式
一旦確定了插值多項式的系數,對于函數f,如果我們想知道某個點處的函數值,只需要對多項式求值即可。
比如,已知函數f在4個點處的函數值:x0=-3.0,f(x0)=-5.0;x1=-2.0,f(x1)=-1.1;x2=2.0,f(x2)=1.9;x3=3.0,f(x3)=4.8;現在要求出點z0=-2.5,z1=0.0,z2=1.0,z3=2.5處的函數值。由于已經知道函數f在4個點處的值,因此插值多項式為3階。下圖是3階插值多項式p3(z)的差商表。

一旦從差商表中得到了系數,就可以采用前面介紹過的牛頓公式來構建插值多項式p3(z):
p3(z)=-5.0 + 3.9(z+3.0) + (-0.63)(z+3.0)(z+2.0) + 0.1767(z+3.0)(z+2.0)(z-2.0)
下一步可以通過該多項式計算出每個點z處的函數值。比如,在點z=-2.5處,經過如下計算得到:
p3(z)=-5.0 + 3.9(-2.5+3.0) + (-0.63)(-2.5+3.0)(-2.5+2.0) + 0.1767(-2.5+3.0)(-2.5+2.0)(-2.5-2.0) = -2.694
點z1、z2、z3處的函數值可以通過相似的方法計算得出。最終結果以表格和函數圖像的方式表達。如下圖。
和任何其他近似算法一樣,通常會有一些與插值多項式相關的誤差出現,理解這一點很重要。定性的來講,如果要使誤差降至最小,構建的插值多項式必須要在函數f(x)上獲取足夠多的已知點才行。并且點與點之前的距離要適當,這樣最終得到的多項式才能精確地表示出函數的特性。
多項式插值的接口定義
interpol
int interpol ( const double *x, const double *fx, int n, double *z, double *pz, int m );
返回值:如果插值操作成功,返回0;否則返回-1;
描述:采用多項式插值法來求得函數在某些特定點上的值。
由調用者在參數x處指定函數值已知的點集。每個已知點所對應的函數值都在fx中指定。對應待求的點由參數z來指定,而z所對應的函數值將在pz中返回。x和f(x)中的元素個數由參數n來表示。z中的待求點的個數(以及pz中返回值個數)由參數m來表示。由調用者管理x、fx、z以及pz所關聯的存儲空間。
復雜度:O(mn2),這里m代表待求值的個數,而n代表已知點的個數。
多項式插值的實現與分析
多項式插值法主要基于對一系列期望點的插值多項式的確定。要得到這個多項式,首先必須通過計算差商來確定該多項式的系數。
首先,為差商以及待確定的系數分配存儲空間。注意,由于差商表中每一行的每一項都僅依賴于其前一行的計算結果,因此,并不需要一次性保留所有的表項。所以,只為最占用空間的行分配空間即可,該行將有n個條目。
接下來,用fx中的值來初始化差商表的第一行。這是為計算差商表中的第三行做準備。(前兩行不需要計算,因為這兩行中的條目都已經保存在x和fx中)。
初始化的最后一步是在coeff[0]中保存fx[0]的值,因為這是插值多項式的第一個系數。
計算差商的過程涉及一個嵌套循環,我們在循環中根據前面介紹過的公式來計算差商。在外層循環中,k用來統計正在計算的是哪一行(排除x和fx所代表的行)。在內層循環中,i表示在當前行中正在計算的是哪一個條目。一旦計算完一行的條目,table[0]中的值就成為插值多項式的下一個系數。因此,保存該值到coeff[k]中。一旦得到插值多項式的所有系數,就可以計算出z中每個目標點的值,最后將這些值保存在pz中。
?我們命名這個函數為interpol,它的時間復雜度為O(mn2),這里m代表z中的元素個數(也是pz中值的個數),n代表x中(也是fx中)的元素個數。復雜度因子n2是這樣得到的,變更j控制循環中的每次迭代,當前迭代中需要乘以的因子比上一輪要多一個。也就是說,當j=1時,term需要做1次乘法,當j=2時,term需要做2次乘法,持續這個過程直到j=n-1時,term需要做n-1次乘法。實際上,這就成了對1~n-1的整數求和,得到的計算時間為T(n)=(n(n+1)/2)-n,再乘以某段固定的時間。(這是由計算等差數列的著名公式得到的)。在大O記法中可以簡化為O(n2)。O(mn2)中的因子m來源于針對z中的每個點計算多項式插值的過程。在第一個嵌套循環中,計算出所有的差商,其復雜度為O(n2)。因此,最終的復雜度有一個額外的因子m,該因子對實際的復雜度沒有多大的影響。
示例:多項式插值的實現
/*interpol.c*/ #include <stdlib.h> #include <string.h>#include "nummeths.h"/*interpol */ int interpol(const double *x, const double *fx, int n, double *z, double *pz, int m) {double term, *table, *coeff;int i,j,k;/*為差商和待確定的系數分配空間*/if((table = (double *)malloc(sizeof(double)*n)) == NULL)return -1;if((coeff = (double *)malloc(sizeof(double)*n)) == NULL){free(table);return -1;}/*初始化差商表*/memcpy(table,fx,sizeof(double)*n);/*重點:確定差商表的系數*/coeff[0] = table[0];for(k=1; k<n; k++)/*外層循環k用來統計正在計算的是哪一行*/{for(i=0; i<n-k; i++)/*內層循環i表示在當前行中正在計算的是哪一個條目(隨之行數的增加,條目減少)*/{j=i+k;/*當前行的每一項中分子的差商就是其前一階段計算的結果*/table[i] = (table[i+1] - table[i]) / (x[j] - x[i]);}/*當前行的首個條目計算結果即是多項式的下一個系數*/coeff[k]=table[0];}free(table);/*在指定點上對插值多項式進行求值(循環構造插值多項式)*/for(k=0; k<m; k++) /*最外層:遍歷z點數組*/{/*插值多項式的第一個因子*/pz[k] = coeff[0]; for(j=1; j<n; j++) /*嵌套:構造多項式(新算式等于上一步的結果加上新因子)*/{term = coeff[j]; /*因子構成:以多項式系數為基礎*/for(i=0; i<j; i++) /*嵌套:新因子以上一步的結果乘以(z[k] - x[i])*/term=term*(z[k] - x[i]);pz[k]=pz[k] + term;}}free(coeff);return 0; }
?



![[NOI2012]騎行川藏](http://pic.xiahunao.cn/[NOI2012]騎行川藏)




”運算符)

)


)

Hello World)



