轉自周見智
介紹
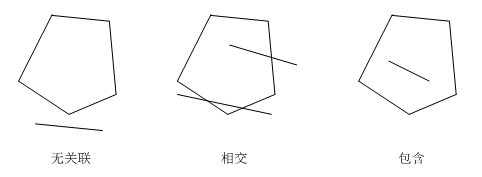
最近項目中要用到有關幾何(Geometry)方面的知識,程序需要判斷給定的一條線段(Segment)與指定多邊形(Polygon)的位置關系。這種關系分為三種:多邊形包含線段、多邊形與線段相交以及多邊形與線段無關聯。
起初我以為.NET類庫中已經包含此種判定功能的API,比如類似System.Drawing.Region這些類型,后來等到實際要用的時候才發現根本就沒這種“高級”算法。
沒辦法,只能自己去寫代碼實現。后來在stackoverflow(鏈接)上找到了一個解決方案,不過都是源代碼,并沒有詳細的說明。本文參照原作者提供的源碼,進行詳細的說明。如果你只需要最終答案,可以不用閱讀本文所有內容,文章最后會給出判斷源代碼,很簡答使用,就一個方法,代入參數直接調用即可,但如果你想搞清楚怎么回事,那么可以靜下心來看看本文全部內容,雖然比較復雜,但是相信一定會有所收獲的。
?
解決思路
線段與多邊形的關系只有三種:無關聯、相交以及包含。我們可以分以下兩步來進行分析:
- 判斷線段與多邊形的各條邊是否相交,若是,則線段與多邊形屬于“相交”關系;
- 如果線段與多邊形的任何邊都不相交,那么我們接著判斷線段的任意一個端點是否在多邊形內部,若是,則整條線段肯定在多邊形內(即“包含”關系);若不是,則整條線段肯定都在多邊形外部(即“無關聯”關系)。
上面兩步看似簡單,實質相當復雜。判斷線段與多邊形各條邊的關系涉及到了“線段與線段關系的判斷”、判斷線段任意一個端點是否在多邊形內部涉及到了“點與線段關系的判斷”,總之,要解決大問題必須先解決一些小問題:
- 點與線段的關系
- 線段與線段的關系
- 點與多邊形的關系
下面依次介紹以上三個小問題的解決方法。
?
問題一:點與線段的關系
點與線段只有兩種關系:
- 點在線段上
- 點與線段無關聯
這種判斷方法很簡單,只要我們能確保給定點P的Y坐標在線段AB兩個端點的Y坐標之間(或者點P的X坐標在兩個端點的X坐標之間也行),并且點P與線段AB任意端點間的斜率與AB線段斜率相等即可說明點P在線段AB上。
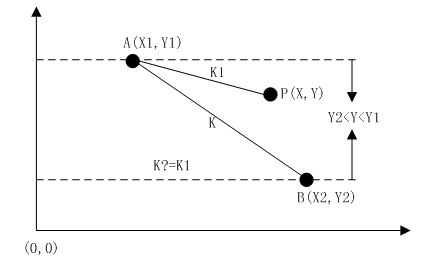
如上圖,如果Y2<Y<Y1且K==K1,則說明點P在線段AB上;否則,點P與線段AB無關聯。
?
問題二:線段與線段的關系
線段與線段也只有兩種關系:
- 兩線段相交
- 兩線段無關聯
這種判斷稍微復雜一些,為了更方便計算,涉及到了“平移”、“旋轉”等操作。給定線段AB和CD,先將兩線段整體平移(注意是整體),讓線段AB的A端點與原點(0,0)重合,接著將兩線段整體旋轉(注意是整體),讓線段AB與X軸的正方向重合。

如上圖,將任意兩線段AB和CD按照“先整體平移,再整體旋轉”的順序操作一遍,最終讓線段AB的A端點與原點(0,0)重合,并讓線段AB與X軸正方向重合。很顯然,任意線段均可以進行以上操作。接下來,再在此基礎上進行判斷就比較簡單了,如果線段CD的兩個端點C和D的Y坐標均大于零(分布在第一、二象限)或者均小于零(分布在第三、四象限),那么AB與CD肯定不相交,換句話說,CD的兩個端點必須一個在X軸上方另一個在X軸下方時,兩條線段才有可能相交。如果線段CD的端點確實是一個在X軸上方一個在X軸下方,接下來再計算直線AB和直線CD(注意這里說的是直線)的交點(這時候兩條直線一定有交點,并且交點在X軸上),這里暫定交點為P,如果P在X軸的負方向上(P.X<0),那么說明線段AB和CD不相交,如果P在X軸正方向但是P的X坐標大于線段AB的長度,那么說明線段AB和CD也不相交,其他情況下,線段AB和CD才屬于“相交”關系。
?
問題三:點與多邊形的關系
點與多邊形有三種關系:
- 點與多邊形無關聯
- 點在多邊形上(某條邊上)
- 點在多邊形內部
判斷點是否在多邊形上需要用到解決問題一的方法,即判斷點與線段的關系。如果點不在多邊形上,那么需要判斷它在多邊形內部還是外部,這個判斷方法說難也不難,說不難也挺難的。事實上,只需要判斷點在多邊形每條邊的左邊還是右邊(注意這里的左邊和右邊定義,見下圖)
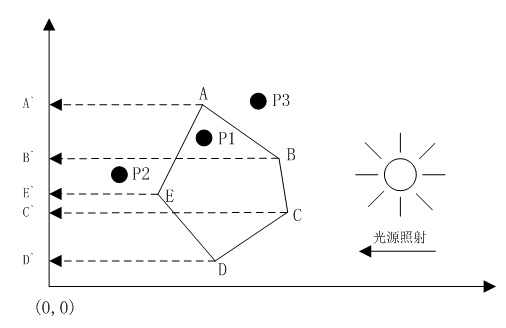
如上圖,多邊形ABCDE在右側光源的照射下,它的每條邊(如AB、BC等)都會與Y軸上各自的投影(如A`B`、B`C`等)之間形成一個梯形區域,如ABB`A`、BCC`B`等。我們只需要統計給定點P在這些梯形區域中的次數,若點P在某條邊對應的梯形區域內,那么計數N加1,最后看N是否為偶數,如果N為偶數(包括0),那么說明點P不在多邊形內部;否則,點P在多邊形內部。上圖中P1的計數N==1(只在ABB`A`內部),所以點P1在多邊形ABCDE內部,而點P2的計數N==2(同時在AEE`A`和BCC`B`內部),所以點P2不在多邊形ABCDE內部,同理,點P3的計數N==0,所以它也不在多邊形內部。
?








)










