離散余弦變換(Discrete Cosine Transform,簡稱DCT變換)是一種與傅立葉變換緊密相關的數學運算。在傅立葉級數展開式中,如果被展開的函數是實偶函數,那么其傅立葉級數中只包含余弦項,再將其離散化可導出余弦變換,因此稱之為離散余弦變換。
離散余弦變換(Discrete Cosine Transform)
離散余弦變換(DCT)是N.Ahmed等人在1974年提出的正交變換方法。它常被認為是對語音和圖像信號進行變換的最佳方法。為了工程上實現的需要,國內外許多學者花費了很大精力去尋找或改進離散余弦變換的快速算法。由于近年來 數字信號處理芯片(DSP)的發展,加上 專用集成電路設計上的優勢,這就牢固地確立離散余弦變換(DCT)在目前圖像編碼中的重要地位,成為H.261、JPEG、MPEG 等國際上公用的編碼標準的重要環節。在視頻壓縮中,最常用的變換方法是DCT,DCT被認為是性能接近K-L變換的準最佳變換,變換編碼的主要特點有: (1)在變換域里視頻圖像要比空間域里簡單。 (2)視頻圖像的相關性明顯下降,信號的能量主要集中在少數幾個變換系數上,采用量化和 熵編碼可有效地壓縮其數據。 (3)具有較強的抗干擾能力,傳輸過程中的誤碼對圖像質量的影響遠小于預測編碼。通常,對高質量的圖像,DMCP要求信道誤碼率 ,而變換編碼僅要求信道誤碼率 。 DCT等變換有快速算法,能實現實時視頻壓縮。針對目前采用的幀內編碼加 運動補償的視頻壓縮方法的不足, 我們在Westwater 等人提出三維 視頻編碼的基礎上, 將三維變換的結構應用于視頻 圖像壓縮, 進一步實現了新的視頻圖像序列的編碼方法。離散余弦變換(英語:DCT for Discrete Cosine Transform)是與傅里葉變換相關的一種變換,它類似于離散傅里葉變換(DFT for Discrete Fourier Transform),但是只使用實數。離散余弦變換相當于一個長度大概是它兩倍的離散傅里葉變換,這個離散傅里葉變換是對一個實偶函數進行的(因為一個實偶函數的傅里葉變換仍然是一個實偶函數),在有些變形里面需要將輸入或者輸出的位置移動半個單位(DCT有8種標準類型,其中4種是常見的)。
最常用的一種離散余弦變換的類型是下面給出的第二種類型,通常我們所說的離散余弦變換指的就是這種。它的逆,也就是下面給出的第三種類型,通常相應的被稱為"反離散余弦變換","逆離散余弦變換"或者"IDCT"。
有兩個相關的變換,一個是離散正弦變換(DST for Discrete Sine Transform),它相當于一個長度大概是它兩倍的實奇函數的離散傅里葉變換;另一個是改進的離散余弦變換(MDCT for Modified Discrete Cosine Transform),它相當于對交疊的數據進行離散余弦變換。
離散余弦變換(英語:DCT for Discrete Cosine Transform)是與傅里葉變換相關的一種變換,它類似于離散傅里葉變換(DFT for Discrete Fourier Transform),但是只使用實數。離散余弦變換相當于一個長度大概是它兩倍的離散傅里葉變換,這個離散傅里葉變換是對一個實偶函數進行的(因為一個實偶函數的傅里葉變換仍然是一個實偶函數),在有些變形里面需要將輸入或者輸出的位置移動半個單位(DCT有8種標準類型,其中4種是常見的)。
最常用的一種離散余弦變換的類型是下面給出的第二種類型,通常我們所說的離散余弦變換指的就是這種。它的逆,也就是下面給出的第三種類型,通常相應的被稱為"反離散余弦變換","逆離散余弦變換"或者"IDCT"。
有兩個相關的變換,一個是離散正弦變換(DST for Discrete Sine Transform),它相當于一個長度大概是它兩倍的實奇函數的離散傅里葉變換;另一個是改進的離散余弦變換(MDCT for Modified Discrete Cosine Transform),它相當于對交疊的數據進行離散余弦變換。
目錄
|
應用
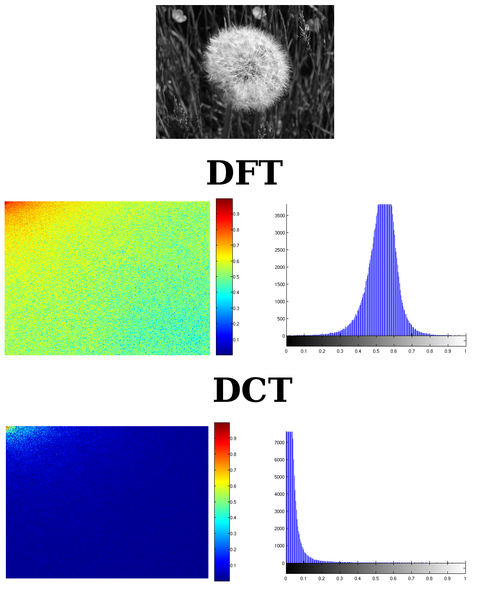
離散余弦變換,尤其是它的第二種類型,經常被信號處理和圖像處理使用,用于對信號和圖像(包括靜止圖像和運動圖像)進行有損數據壓縮。這是由于離散余弦變換具有很強的"能量集中"特性:大多數的自然信號(包括聲音和圖像)的能量都集中在離散余弦變換后的低頻部分,而且當信號具有接近馬爾可夫過程(Markov processes)的統計特性時,離散余弦變換的去相關性接近于K-L變換(Karhunen-Loève變換——它具有最優的去相關性)的性能。
例如,在靜止圖像編碼標準JPEG中,在運動圖像編碼標準MJPEG和MPEG的各個標準中都使用了離散余弦變換。在這些標準制中都使用了二維的第二種類型離散余弦變換,并將結果進行量化之后進行熵編碼。這時對應第二種類型離散余弦變換中的n通常是8,并用該公式對每個8x8塊的每行進行變換,然后每列進行變換。得到的是一個8x8的變換系數矩陣。其中(0,0)位置的元素就是直流分量,矩陣中的其他元素根據其位置表示不同頻率的交流分量。
一個類似的變換, 改進的離散余弦變換被用在高級音頻編碼(AAC for Advanced Audio Coding),Vorbis 和 MP3 音頻壓縮當中。
離散余弦變換也經常被用來使用譜方法來解偏微分方程,這時候離散余弦變換的不同的變量對應著數組兩端不同的奇/偶邊界條件。
正式定義
形式上來看,離散余弦變換一個線性的可逆函數 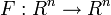 其中R 是實數集, 或者等價的說一個
其中R 是實數集, 或者等價的說一個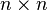 的方陣。離散余弦變換有幾種變形的形式, 它們都是根據下面的某一個公式把
的方陣。離散余弦變換有幾種變形的形式, 它們都是根據下面的某一個公式把 個實數
個實數 變換到另外
變換到另外 個實數
個實數 的操作。
的操作。
DCT-I
有些人認為應該將 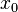 和
和 乘以
乘以 ,相應的將
,相應的將 和
和 乘以
乘以 。這樣做的結果是這種 DCT-I 矩陣變為了 正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個實偶離散傅里葉變換對應了。
。這樣做的結果是這種 DCT-I 矩陣變為了 正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個實偶離散傅里葉變換對應了。
一個 的對實數abcde的DCT-I型變換等價于一個8點的對實數abcdedcb(偶對稱)的DFT變換,結果再除以2(對應的,DCT-II~DCT-IV相對等價的DFT有一個半個抽樣的位移)。需要指出的是,DCT-I不適用于
的對實數abcde的DCT-I型變換等價于一個8點的對實數abcdedcb(偶對稱)的DFT變換,結果再除以2(對應的,DCT-II~DCT-IV相對等價的DFT有一個半個抽樣的位移)。需要指出的是,DCT-I不適用于 的情況(其它的DCT類型都適用于所有的整數n)。
的情況(其它的DCT類型都適用于所有的整數n)。
所以,DCT-I暗示的邊界條件是: 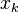 相對于
相對于 點偶對稱,并且相對于
點偶對稱,并且相對于  點偶對稱; 對
點偶對稱; 對 的情況也類似。
的情況也類似。
DCT-II
DCT-II大概是最常用的一種形式,通常直接被稱為DCT。
有些人更進一步的將 再乘以
再乘以 (參見下面的DCT-III型的對應修改)。這將使得DCT-II成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個有半個抽樣位移的實偶離散傅里葉變換對應了。
(參見下面的DCT-III型的對應修改)。這將使得DCT-II成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個有半個抽樣位移的實偶離散傅里葉變換對應了。
所以,DCT-II暗示的邊界條件是: 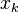 相對于
相對于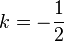 點偶對稱,并且相對于
點偶對稱,并且相對于  點偶對稱; 對
點偶對稱; 對 相對于
相對于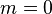 點偶對稱,并且相對于
點偶對稱,并且相對于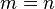 點奇對稱。
點奇對稱。
DCT-III
因為這是DCT-II的逆變換(再乘一個系數的話),這種變形通常被簡單的稱為逆離散余弦變換。
有些人更進一步的將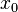 再乘以
再乘以 (參見上面的DCT-II型的對應修改),這將使得DCT-III成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個結果有半個抽樣位移的實偶離散傅里葉變換對應了。
(參見上面的DCT-II型的對應修改),這將使得DCT-III成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個結果有半個抽樣位移的實偶離散傅里葉變換對應了。
所以,DCT-III暗示的邊界條件是: 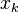 相對于
相對于 點偶對稱,并且相對于
點偶對稱,并且相對于  點奇對稱; 對
點奇對稱; 對 相對于
相對于 點偶對稱,并且相對于
點偶對稱,并且相對于  點奇對稱。
點奇對稱。
DCT-IV
DCT-IV對應的矩陣是正交矩陣 (再乘一個系數的話)。
一種DCT-IV的變形,將不同的變換的數據重疊起來,被稱為改進的離散余弦變換。
DCT-IV暗示的邊界條件是: 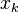 相對于
相對于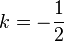 點偶對稱,并且相對于
點偶對稱,并且相對于  點奇對稱;對
點奇對稱;對 類似。
類似。
DCT V~VIII
上面提到的DCT I~IV是和偶數階的實偶DFT對應的。原則上,還有四種DCT變換(Martucci, 1994)是和奇數階的實偶DFT對應的,它們在分母中都有一個 的系數。但是在實際應用中,這幾種變型很少被用到。
的系數。但是在實際應用中,這幾種變型很少被用到。
最平凡的和奇數階的實偶DFT對應的DCT是1階的DCT (1也是奇數),可以說變換只是乘上一個系數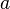 而已,對應于DCT-V的長度為1的狀況。
而已,對應于DCT-V的長度為1的狀況。
反變換
DCT-I的反變換是把DCT-I乘以系數 。 DCT-IV的反變換是把DCT-IV乘以系數
。 DCT-IV的反變換是把DCT-IV乘以系數 。 DCT-II的反變換是把DCT-III乘以系數
。 DCT-II的反變換是把DCT-III乘以系數 ,反之亦然。
,反之亦然。
和離散傅里葉變換類似,變化前面的歸一化系數僅僅是常規而已,改變這個系數并不改變變換的性質。例如,有些人喜歡在DCT-II變換的前面乘以 ,這樣反變換從形式上就和變換更相似,而不需要另外的歸一化系數。
,這樣反變換從形式上就和變換更相似,而不需要另外的歸一化系數。
計算
盡管直接使用公式進行變換需要進行 次操作,但是和快速傅里葉變換類似,我們有復雜度為
次操作,但是和快速傅里葉變換類似,我們有復雜度為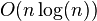 的快速算法,這就是常常被稱做蝶形變換的一種分解算法。另外一種方法是通過快速傅里葉變換來計算DCT,這時候需要
的快速算法,這就是常常被稱做蝶形變換的一種分解算法。另外一種方法是通過快速傅里葉變換來計算DCT,這時候需要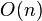 的預操作和后操作。
的預操作和后操作。
參考
- K. R. Rao and P. Yip, 離散余弦變換?: 算法、優點和應用 (Discrete Cosine Transform: Algorithms, Advantages, Applications) (Academic Press, Boston, 1990).
- A. V. Oppenheim, R. W. Schafer, and J. R. Buck, 時間離散信號處理 (Discrete-Time Signal Processing), second edition (Prentice-Hall, New Jersey, 1999).
- S. A. Martucci, 對稱卷積和離散正弦余弦變換 (Symmetric convolution and the discrete sine and cosine transforms),IEEE Trans. Sig. Processing SP-42, 1038-1051 (1994).
- Matteo Frigo and Steven G. Johnson: FFTW, http://www.fftw.org/. 一個免費的C語言庫GPL,可以計算DCT-I~IV的1維到多維的任意大小的變換
- M. Frigo and S. G. Johnson, "FFTW3的設計和實現,"Proceedings of the IEEE 93 (2), 216–231 (2005).
目錄
|
應用
離散余弦變換,尤其是它的第二種類型,經常被信號處理和圖像處理使用,用于對信號和圖像(包括靜止圖像和運動圖像)進行有損數據壓縮。這是由于離散余弦變換具有很強的"能量集中"特性:大多數的自然信號(包括聲音和圖像)的能量都集中在離散余弦變換后的低頻部分,而且當信號具有接近馬爾可夫過程(Markov processes)的統計特性時,離散余弦變換的去相關性接近于K-L變換(Karhunen-Loève變換——它具有最優的去相關性)的性能。
例如,在靜止圖像編碼標準JPEG中,在運動圖像編碼標準MJPEG和MPEG的各個標準中都使用了離散余弦變換。在這些標準制中都使用了二維的第二種類型離散余弦變換,并將結果進行量化之后進行熵編碼。這時對應第二種類型離散余弦變換中的n通常是8,并用該公式對每個8x8塊的每行進行變換,然后每列進行變換。得到的是一個8x8的變換系數矩陣。其中(0,0)位置的元素就是直流分量,矩陣中的其他元素根據其位置表示不同頻率的交流分量。
一個類似的變換, 改進的離散余弦變換被用在高級音頻編碼(AAC for Advanced Audio Coding),Vorbis 和 MP3 音頻壓縮當中。
離散余弦變換也經常被用來使用譜方法來解偏微分方程,這時候離散余弦變換的不同的變量對應著數組兩端不同的奇/偶邊界條件。
正式定義
形式上來看,離散余弦變換一個線性的可逆函數 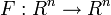 其中R 是實數集, 或者等價的說一個
其中R 是實數集, 或者等價的說一個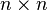 的方陣。離散余弦變換有幾種變形的形式, 它們都是根據下面的某一個公式把
的方陣。離散余弦變換有幾種變形的形式, 它們都是根據下面的某一個公式把 個實數
個實數 變換到另外
變換到另外 個實數
個實數 的操作。
的操作。
DCT-I
有些人認為應該將 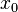 和
和 乘以
乘以 ,相應的將
,相應的將 和
和 乘以
乘以 。這樣做的結果是這種 DCT-I 矩陣變為了 正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個實偶離散傅里葉變換對應了。
。這樣做的結果是這種 DCT-I 矩陣變為了 正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個實偶離散傅里葉變換對應了。
一個 的對實數abcde的DCT-I型變換等價于一個8點的對實數abcdedcb(偶對稱)的DFT變換,結果再除以2(對應的,DCT-II~DCT-IV相對等價的DFT有一個半個抽樣的位移)。需要指出的是,DCT-I不適用于
的對實數abcde的DCT-I型變換等價于一個8點的對實數abcdedcb(偶對稱)的DFT變換,結果再除以2(對應的,DCT-II~DCT-IV相對等價的DFT有一個半個抽樣的位移)。需要指出的是,DCT-I不適用于 的情況(其它的DCT類型都適用于所有的整數n)。
的情況(其它的DCT類型都適用于所有的整數n)。
所以,DCT-I暗示的邊界條件是: 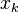 相對于
相對于 點偶對稱,并且相對于
點偶對稱,并且相對于  點偶對稱; 對
點偶對稱; 對 的情況也類似。
的情況也類似。
DCT-II
DCT-II大概是最常用的一種形式,通常直接被稱為DCT。
有些人更進一步的將 再乘以
再乘以 (參見下面的DCT-III型的對應修改)。這將使得DCT-II成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個有半個抽樣位移的實偶離散傅里葉變換對應了。
(參見下面的DCT-III型的對應修改)。這將使得DCT-II成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個有半個抽樣位移的實偶離散傅里葉變換對應了。
所以,DCT-II暗示的邊界條件是: 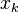 相對于
相對于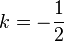 點偶對稱,并且相對于
點偶對稱,并且相對于  點偶對稱; 對
點偶對稱; 對 相對于
相對于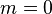 點偶對稱,并且相對于
點偶對稱,并且相對于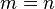 點奇對稱。
點奇對稱。
DCT-III
因為這是DCT-II的逆變換(再乘一個系數的話),這種變形通常被簡單的稱為逆離散余弦變換。
有些人更進一步的將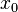 再乘以
再乘以 (參見上面的DCT-II型的對應修改),這將使得DCT-III成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個結果有半個抽樣位移的實偶離散傅里葉變換對應了。
(參見上面的DCT-II型的對應修改),這將使得DCT-III成為正交矩陣 (再乘一個系數的話),但是這樣就不能直接和一個結果有半個抽樣位移的實偶離散傅里葉變換對應了。
所以,DCT-III暗示的邊界條件是: 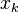 相對于
相對于 點偶對稱,并且相對于
點偶對稱,并且相對于  點奇對稱; 對
點奇對稱; 對 相對于
相對于 點偶對稱,并且相對于
點偶對稱,并且相對于  點奇對稱。
點奇對稱。
DCT-IV
DCT-IV對應的矩陣是正交矩陣 (再乘一個系數的話)。
一種DCT-IV的變形,將不同的變換的數據重疊起來,被稱為改進的離散余弦變換。
DCT-IV暗示的邊界條件是: 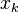 相對于
相對于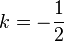 點偶對稱,并且相對于
點偶對稱,并且相對于  點奇對稱;對
點奇對稱;對 類似。
類似。
DCT V~VIII
上面提到的DCT I~IV是和偶數階的實偶DFT對應的。原則上,還有四種DCT變換(Martucci, 1994)是和奇數階的實偶DFT對應的,它們在分母中都有一個 的系數。但是在實際應用中,這幾種變型很少被用到。
的系數。但是在實際應用中,這幾種變型很少被用到。
最平凡的和奇數階的實偶DFT對應的DCT是1階的DCT (1也是奇數),可以說變換只是乘上一個系數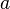 而已,對應于DCT-V的長度為1的狀況。
而已,對應于DCT-V的長度為1的狀況。
反變換
DCT-I的反變換是把DCT-I乘以系數 。 DCT-IV的反變換是把DCT-IV乘以系數
。 DCT-IV的反變換是把DCT-IV乘以系數 。 DCT-II的反變換是把DCT-III乘以系數
。 DCT-II的反變換是把DCT-III乘以系數 ,反之亦然。
,反之亦然。
和離散傅里葉變換類似,變化前面的歸一化系數僅僅是常規而已,改變這個系數并不改變變換的性質。例如,有些人喜歡在DCT-II變換的前面乘以 ,這樣反變換從形式上就和變換更相似,而不需要另外的歸一化系數。
,這樣反變換從形式上就和變換更相似,而不需要另外的歸一化系數。
計算
盡管直接使用公式進行變換需要進行 次操作,但是和快速傅里葉變換類似,我們有復雜度為
次操作,但是和快速傅里葉變換類似,我們有復雜度為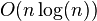 的快速算法,這就是常常被稱做蝶形變換的一種分解算法。另外一種方法是通過快速傅里葉變換來計算DCT,這時候需要
的快速算法,這就是常常被稱做蝶形變換的一種分解算法。另外一種方法是通過快速傅里葉變換來計算DCT,這時候需要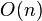 的預操作和后操作。
的預操作和后操作。
參考
- K. R. Rao and P. Yip, 離散余弦變換?: 算法、優點和應用 (Discrete Cosine Transform: Algorithms, Advantages, Applications) (Academic Press, Boston, 1990).
- A. V. Oppenheim, R. W. Schafer, and J. R. Buck, 時間離散信號處理 (Discrete-Time Signal Processing), second edition (Prentice-Hall, New Jersey, 1999).
- S. A. Martucci, 對稱卷積和離散正弦余弦變換 (Symmetric convolution and the discrete sine and cosine transforms),IEEE Trans. Sig. Processing SP-42, 1038-1051 (1994).
- Matteo Frigo and Steven G. Johnson: FFTW, http://www.fftw.org/. 一個免費的C語言庫GPL,可以計算DCT-I~IV的1維到多維的任意大小的變換
- M. Frigo and S. G. Johnson, "FFTW3的設計和實現,"Proceedings of the IEEE 93 (2), 216–231 (2005).
![f_m = \frac{1}{2} (x_0 + (-1)^m x_{n-1}) + \sum_{k=1}^{n-2} x_k \cos \left[\frac{\pi}{n-1} m k \right]](http://upload.wikimedia.org/wikipedia/zh/math/d/9/e/d9e60bdf9342f4d92d51cda2eda577e5.png)
![f_m = \sum_{k=0}^{n-1} x_k \cos \left[\frac{\pi}{n} m \left(k+\frac{1}{2}\right) \right]](http://upload.wikimedia.org/wikipedia/zh/math/7/2/c/72cf9eb1d084ee7f5b49d959c2f7f914.png)
![f_m = \frac{1}{2} x_0 + \sum_{k=1}^{n-1} x_k \cos \left[\frac{\pi}{n} \left(m+\frac{1}{2}\right) k \right]](http://upload.wikimedia.org/wikipedia/zh/math/2/d/2/2d2100c86683f21dfc884919549406fc.png)
![f_m = \sum_{k=0}^{n-1} x_k \cos \left[\frac{\pi}{n} \left(m+\frac{1}{2}\right) \left(k+\frac{1}{2}\right) \right]](http://upload.wikimedia.org/wikipedia/zh/math/4/b/d/4bdad73069401c796d99f3b87f644e50.png)



)









)



![[Python] 程序結構與控制流](http://pic.xiahunao.cn/[Python] 程序結構與控制流)

