leetcood學習筆記-204-計算質數

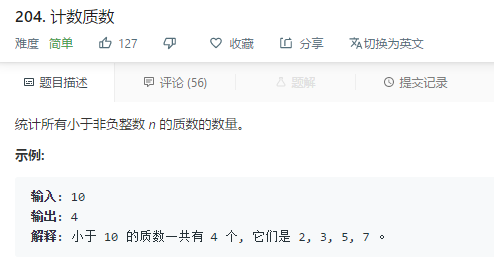
題目描述：

?

第一次提交;(超時)：

class Solution:def countPrimes(self, n: int) -> int:count = 0for i in range(2,n):for j in range(2,i+1):if i%j == 0 and j!=i:breakif j==i:count+=1return count

別人家的：

這題搜到一個非常牛逼的算法,叫做厄拉多塞篩法. 比如說求20以內質數的個數,首先0,1不是質數.2是第一個質數,然后把20以內所有2的倍數劃去.2后面緊跟的數即為下一個質數3,然后把3所有的倍數劃去.3后面緊跟的數即為下一個質數5,再把5所有的倍數劃去.以此類推.代碼的實現上用了非常好的技巧:def countPrimes(self, n: int) -> int:if n < 3:return 0     else:# 首先生成了一個全部為1的列表output = [1] * n# 因為0和1不是質數,所以列表的前兩個位置賦值為0output[0],output[1] = 0,0# 此時從index = 2開始遍歷,output[2]==1,即表明第一個質數為2,然后將2的倍數對應的索引# 全部賦值為0. 此時output[3] == 1,即表明下一個質數為3,同樣劃去3的倍數.以此類推.for i in range(2,int(n**0.5)+1): if output[i] == 1:output[i*i:n:i] = [0] * len(output[i*i:n:i]) #注意[0]# 最后output中的數字1表明該位置上的索引數為質數,然后求和即可.return sum(output)
在上面遍歷索引的時候用到了一個非常好的技巧. 即i是從(2,int(n**0.5)+1)而非(2,n).這個技巧是可以驗證的,比如說求9以內的質數個數,那么只要劃掉sqrt(9)以內的質數倍數,剩下的即全為質數. 所以在劃去倍數的時候也是從i*i開始劃掉,而不是i+i.

?