我們知道，在一個容量為n的數據集合中尋找一個最大數，不管用什么樣的比較算法，至少要比較n-1次，就算是用競標賽排序也得比較n-1次，否則你找到的就不能保證是最大的數。那么，在一個容量為n的數據集合中同時尋找最大數和最小數的最小比較次數是多少呢？
???? 從一個容量為n的數據集合中同時找到最大數和最小數的最優方法是：首先讓所有的元素參與兩兩比較，這樣總共比較了n/2次，最大數肯定在勝者組中，最小數肯定在敗者組中；然后從容量為n/2的勝者組中找到最大的數，最少要比較n/2 - 1次；同理，從容量為n/2的敗者組中找到最小的數，最少要比較n/2 - 1次。所以總共需要比較 (3n/2) - 2次。以上假設n為偶數。奇數同理。

這是同時尋找最大數和最小數的最優算法。

?

??? 那么，我們要從一個容量為n的數據集（假設該數據集是一個集合，即沒有相同的元素）中找到第二大元素需要多少次比較呢？
??? 一種習慣的方法是：先找出最大的元素，這需要比較n-1次；然后從剩下的n-1個元素中找到最大的，這個元素就是我們要找的第二大元素，這需要比較n-2次。做一總共比較2n-3次。
但是，
??? 還有一個更優的方法：
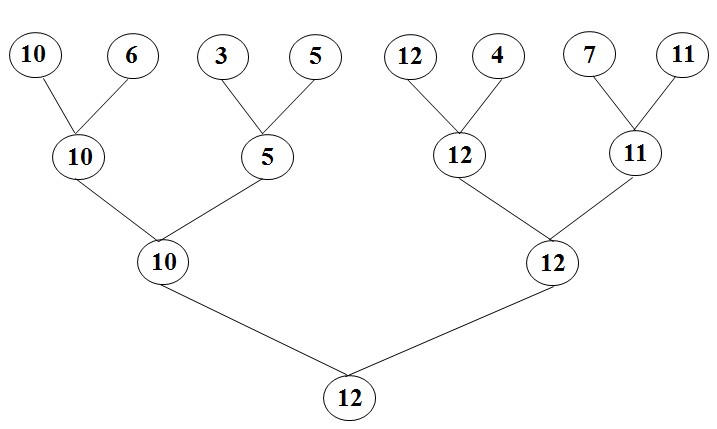
（1） 我們考慮淘汰賽的比較法，淘汰賽結束后，找出冠軍我們需要n-1次比較；如下圖所示，找到12需要比較7次。
（2） 此時我們要考慮到，亞軍應該存在于敗給冠軍的這些選手中（否則，每個元素都至少有兩個元素比它大），由于與冠軍比過的元素個數為┌log2n┐，從這些元素中找到最大值需要比較┌log2n┐ - 1次；如下圖所示，亞軍應該在10,11,4這三個元素中。否則，如果亞軍是5，那么冠軍12比它大，與它比較過的10也比它大，至少兩個元素大于5，所以5肯定不是亞軍的候選者。

?

（3）從而找出亞軍要比較n-1+┌log2n┐-1 = n-2+┌log2n┐次比較。這個算法是尋找亞軍的最優算法。

分治與遞歸——最大值和次大值的最優算法

問題描述：輸入n個數，最壞情況下用?n + logn - 2?次比較找出當中的最大值和次大值。

算法思想：根據題意出現logn，則肯定用到二分或者堆的思路，但是輸入的數沒有經過排序，而且題目要求的計算量也不允許排序。這樣，就肯定會用到類似堆的思路，但是直接構造堆等同于排序。堆的思想跟競標賽類似，都是父節點>=（<=）子節點。如果父節點都是從子節點而來，這樣就是競標賽；如果不是，這樣就是堆。既然不能排序又不能構造堆，那就只能用競標賽的思想，通過二分來進行最多logn次競賽，選出最大值（冠軍），而次大值（亞軍）只能在與最大值的比較中被淘汰（亞軍的實力只可能輸給冠軍），故在所有被最大值（冠軍）淘汰的數值中選取次大值，最多也是logn次比較，滿足題意（由于題意只限制了比較次數，故實現過程并沒有考慮時間復雜度和空間復雜度）

代碼實現：

//最大值和次大值的最優算法,數組中可能存在重復元素,不能處理最大值是0的情況

#include <stdio.h>

#define N 1000

int m[2*N];

int num[2*N];

int biaoji[N];

int bigger(int i)

{

????if(num[i]>num[i+1])

????{

????????biaoji[m[i+1]]=num[i];

????????return i;

????}

????else

????{

????????biaoji[m[i]]=num[i+1];

????????return i+1;

????}

}

int work(int a,int b)

{

????int i,j;

????while(a<b)

????{

????????for(i=a;i<b;i+=2)

????????{

????????????j=bigger(i);

????????????num[i/2]=num[j];

????????????m[i/2]=m[j];

????????}

????????if(i==b)

????????{

????????????num[i/2]=num[i];

????????????m[i/2]=m[i];

????????}

????????a=a/2;

????????b=b/2;

????}

????return num[a];

}

int work2(int l,int max)

{

????int i,flag=1;

????int bmax;

????for(i=l;i<2*l;++i)

????{

????????if(biaoji[i-l]==max)

????????{

????????????if(flag)

????????????{

????????????????flag=0;

????????????????bmax=num[i];

????????????}

????????????else if(bmax<num[i])

????????????????bmax=num[i];

????????}

????}

????return bmax;

}

int main()

{

????int i,l;

????int max,bmax;

????int f,start;

????while(true)

????{

????????printf("please putin the length:\n");

????????scanf("%d",&l);

????????if(l==0)

????????????break;

????????printf("please putin num[]:\n");

????????for(i=l;i<2*l;++i)

????????????scanf("%d",&num[i]);

????????for(i=l;i<2*l;++i)

????????????m[i]=(i-l);

????????max=work(l,2*l-1);

????????bmax=work2(l,max);

????????printf("the max is %d and the bmax is %d\n",max,bmax);

????}

?

????return 0;

}