數據結構與算法-概念

計算機從解決數值計算問題到解決生活中的問題
現實生活中的問題涉及不同個體間的復雜聯系
需要在計算機程序中描述生活中個體間的聯系
數據結構主要研究非數值計算程序問題中的操作對象以及它們之間的關系而不是研究復雜的算法

數據結構

基本概念

數據：程序的操作對象，用于描述客觀事物

數據的特點：
-可以輸入到計算機
-可以被計算機程序處理

數據是一個抽象的概念，將其進行分類后得到程序設計語言中的類型。如：int，float，char等等

數據元素：組成數據的基本單位
數據項：一個數據元素由若干數據項組成
數據對象 – 性質相同的數據元素的集合
e.g.

struct _MyTeacher   //一種數據類型
{char	name[32];char	tile[32];int		age;char	addr[128];
};int main21()
{struct _MyTeacher t1; //數據元素struct _MyTeacher tArray[30]; //數據對象memset(&t1, 0, sizeof(t1));strcpy(t1.name, "name"); //數據項strcpy(t1.addr, "addr"); //數據項strcpy(t1.tile, "addr"); //數據項t1.age = 1;
}

數據元素之間不是獨立的，存在特定的關系，這些關系即結構

數據結構指數據對象中數據元素之間的關系

數據的邏輯結構

指數據元素之間的邏輯關系。即從邏輯關系上描述數據，它與數據的存儲無關，是獨立于計算機的。邏輯結構可細分為4類

數據的物理結構

數據的運算

算法

基本概念

算法是特定問題求解步驟的描述
在計算機中表現為指令的有限序列
算法是獨立存在的一種解決問題的方法和思想
對于算法而言，語言并不重要，重要的是思想

算法和數據結構區別

數據結構只是靜態的描述了數據元素之間的關系
高效的程序需要在數據結構的基礎上設計和選擇算法

程序=數據結構+算法

總結：
算法是為了解決實際問題而設計的
數據結構是算法需要處理的問題載體
數據結構與算法相輔相成

算法特性

• 輸入：算法具有0個或多個輸入
• 輸出：算法至少有1個或多個輸出
• 有窮性：算法在有限的步驟之后會自動結束而不會無限循環
• 確定性：算法中的每一步都有確定的含義，不會出現二義性
• 可行性：算法的每一步都是可行的

算法效率的度量

• 事后統計法
  比較不同算法對同一組輸入數據的運行處理時間
  缺陷

  • 為了獲得不同算法的運行時間必須編寫相應程序
  • 運行時間嚴重依賴硬件以及運行時的環境因素
  • 算法的測試數據的選取相當困難
  • 事后統計法雖然直觀，但是實施困難且缺陷多

• 事前分析估算
  依據統計的方法對算法效率進行估算
  影響算法效率的主要因素

  • 算法采用的策略和方法
  • 問題的輸入規模
  • 編譯器所產生的代碼
  • 計算機執行速度

• 大O表示法
  算法效率嚴重依賴于操作(Operation)數量
  在判斷時首先關注操作數量的最高次項
  操作數量的估算可以作為時間復雜度的估算
  常見時間復雜度：
  
  關系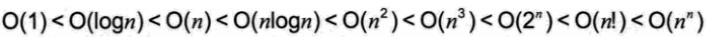
  

• 算法的空間復雜度
  算法的空間復雜度通過計算算法的存儲空間實現
  S(n) = O(f(n))
  其中，n為問題規模，f(n))為在問題規模為nn時所占用存儲空間的函數
  大O表示法同樣適用于算法的空間復雜度
  當算法執行時所需要的空間是常數時，空間復雜度為O(1)

空間與時間的策略

• 多數情況下，算法執行時所用的時間更令人關注
• 如果有必要，可以通過增加空間復雜度來降低時間復雜度
• 同理，也可以通過增加時間復雜度來降低空間復雜度