C#實現A*算法

理解A*尋路算法具體過程

這兩天研究了下 A* 尋路算法, 主要學習了這篇文章, 但這篇翻譯得不是很好, 我花了很久才看明白文章中的各種指代. 特寫此篇博客用來總結, 并寫了尋路算法的代碼, 覺得有用的同學可以看看. 另外因為圖片制作起來比較麻煩, 所以我用的是原文里的圖片.
當然尋路算法不止 A* 這一種, 還有遞歸, 非遞歸, 廣度優先, 深度優先, 使用堆棧等等, 有興趣的可以研究研究~~

簡易地圖

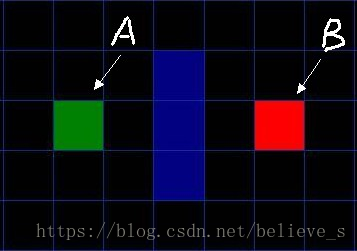
這里寫圖片描述
如圖所示簡易地圖, 其中綠色方塊的是起點 (用 A 表示), 中間藍色的是障礙物, 紅色的方塊 (用 B 表示) 是目的地. 為了可以用一個二維數組來表示地圖, 我們將地圖劃分成一個個的小方塊.
二維數組在游戲中的應用是很多的, 比如貪吃蛇和俄羅斯方塊基本原理就是移動方塊而已. 而大型游戲的地圖, 則是將各種”地貌”鋪在這樣的小方塊上.

尋路步驟

從起點A開始, 把它作為待處理的方格存入一個”開啟列表”, 開啟列表就是一個等待檢查方格的列表.
尋找起點A周圍可以到達的方格, 將它們放入”開啟列表”, 并設置它們的”父方格”為A.
從”開啟列表”中刪除起點 A, 并將起點 A 加入”關閉列表”, “關閉列表”中存放的都是不需要再次檢查的方格

這里寫圖片描述
圖中淺綠色描邊的方塊表示已經加入 “開啟列表” 等待檢查. 淡藍色描邊的起點 A 表示已經放入 “關閉列表” , 它不需要再執行檢查.
從 “開啟列表” 中找出相對最靠譜的方塊, 什么是最靠譜? 它們通過公式 F=G+H 來計算.

F = G + H
G 表示從起點 A 移動到網格上指定方格的移動耗費 (可沿斜方向移動).
H 表示從指定的方格移動到終點 B 的預計耗費 (H 有很多計算方法, 這里我們設定只可以上下左右移動).

這里寫圖片描述

我們假設橫向移動一個格子的耗費為10, 為了便于計算, 沿斜方向移動一個格子耗費是14. 為了更直觀的展示如何運算 FGH, 圖中方塊的左上角數字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的結果一樣?
從 “開啟列表” 中選擇 F 值最低的方格 C (綠色起始方塊 A 右邊的方塊), 然后對它進行如下處理:

把它從 “開啟列表” 中刪除, 并放到 “關閉列表” 中.
檢查它所有相鄰并且可以到達 (障礙物和 “關閉列表” 的方格都不考慮) 的方格. 如果這些方格還不在 “開啟列表” 里的話, 將它們加入 “開啟列表”, 計算這些方格的 G, H 和 F 值各是多少, 并設置它們的 “父方格” 為 C.
如果某個相鄰方格 D 已經在 “開啟列表” 里了, 檢查如果用新的路徑 (就是經過C 的路徑) 到達它的話, G值是否會更低一些, 如果新的G值更低, 那就把它的 “父方格” 改為目前選中的方格 C, 然后重新計算它的 F 值和 G 值 (H 值不需要重新計算, 因為對于每個方塊, H 值是不變的). 如果新的 G 值比較高, 就說明經過 C 再到達 D 不是一個明智的選擇, 因為它需要更遠的路, 這時我們什么也不做.

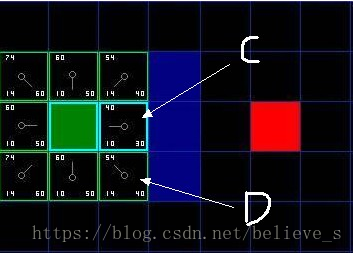
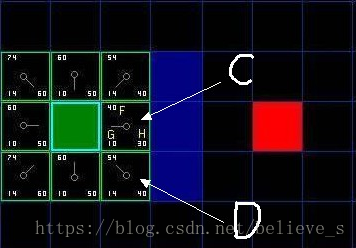
這里寫圖片描述
如圖, 我們選中了 C 因為它的 F 值最小, 我們把它從 “開啟列表” 中刪除, 并把它加入 “關閉列表”. 它右邊上下三個都是墻, 所以不考慮它們. 它左邊是起始方塊, 已經加入到 “關閉列表” 了, 也不考慮. 所以它周圍的候選方塊就只剩下 4 個. 讓我們來看看 C 下面的那個格子, 它目前的 G 是14, 如果通過 C 到達它的話, G將會是 10 + 10, 這比 14 要大, 因此我們什么也不做.
然后我們繼續從 “開啟列表” 中找出 F 值最小的, 但我們發現 C 上面的和下面的同時為 54, 這時怎么辦呢? 這時隨便取哪一個都行, 比如我們選擇了 C 下面的那個方塊 D.
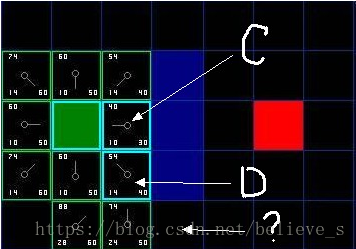
這里寫圖片描述
D 右邊已經右上方的都是墻, 所以不考慮, 但為什么右下角的沒有被加進 “開啟列表” 呢? 因為如果 C 下面的那塊也不可以走, 想要到達 C 右下角的方塊就需要從 “方塊的角” 走了, 在程序中設置是否允許這樣走. (圖中的示例不允許這樣走)
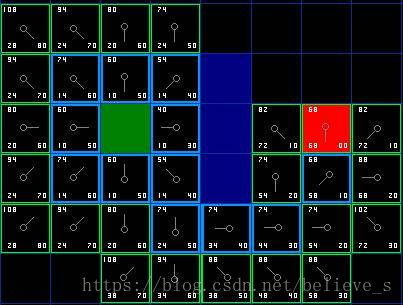
這里寫圖片描述
就這樣, 我們從 “開啟列表” 找出 F 值最小的, 將它從 “開啟列表” 中移掉, 添加到 “關閉列表”. 再繼續找出它周圍可以到達的方塊, 如此循環下去…
那么什么時候停止呢? —— 當我們發現 “開始列表” 里出現了目標終點方塊的時候, 說明路徑已經被找到.

如何找回路徑

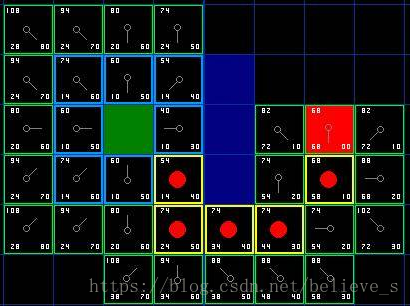
這里寫圖片描述
如上圖所示, 除了起始方塊, 每一個曾經或者現在還在 “開啟列表” 里的方塊, 它都有一個 “父方塊”, 通過 “父方塊” 可以索引到最初的 “起始方塊”, 這就是路徑.

將整個過程抽象

把起始格添加到 “開啟列表”
do
{
尋找開啟列表中F值最低的格子, 我們稱它為當前格.
把它切換到關閉列表.
對當前格相鄰的8格中的每一個
if (它不可通過 || 已經在 “關閉列表” 中)
{
什么也不做.
}
if (它不在開啟列表中)
{
把它添加進 “開啟列表”, 把當前格作為這一格的父節點, 計算這一格的 FGH
if (它已經在開啟列表中)
{
if (用G值為參考檢查新的路徑是否更好, 更低的G值意味著更好的路徑)
{
把這一格的父節點改成當前格, 并且重新計算這一格的 GF 值.
}
} while( 目標格已經在 “開啟列表”, 這時候路徑被找到)
如果開啟列表已經空了, 說明路徑不存在.

最后從目標格開始, 沿著每一格的父節點移動直到回到起始格, 這就是路徑.

主要代碼

程序中的 “開啟列表” 和 “關閉列表”

List<Point> CloseList;
List<Point> OpenList;

Point 類

public class Point
{public Point ParentPoint { get; set; }public int F { get; set; }  //F=G+Hpublic int G { get; set; }public int H { get; set; }public int X { get; set; }public int Y { get; set; }public Point(int x, int y){this.X = x;this.Y = y;}public void CalcF(){this.F = this.G + this.H;}
}

尋路過程

public Point FindPath(Point start, Point end, bool IsIgnoreCorner)
{OpenList.Add(start);while (OpenList.Count != 0){//找出F值最小的點var tempStart = OpenList.MinPoint();OpenList.RemoveAt(0);CloseList.Add(tempStart);//找出它相鄰的點var surroundPoints = SurrroundPoints(tempStart, IsIgnoreCorner);foreach (Point point in surroundPoints){if (OpenList.Exists(point))//計算G值, 如果比原來的大, 就什么都不做, 否則設置它的父節點為當前點,并更新G和FFoundPoint(tempStart, point);else//如果它們不在開始列表里, 就加入, 并設置父節點,并計算GHFNotFoundPoint(tempStart, end, point);}if (OpenList.Get(end) != null)return OpenList.Get(end);}return OpenList.Get(end);
}

完整代碼
maze.cs

using System;
using System.Collections.Generic;
using System.Linq;namespace Maze
{class Maze{public const int OBLIQUE = 14;public const int STEP = 10;public int[,] MazeArray { get; private set; }List<Point> CloseList;List<Point> OpenList;public Maze(int[,] maze){this.MazeArray = maze;OpenList = new List<Point>(MazeArray.Length);CloseList = new List<Point>(MazeArray.Length);}public Point FindPath(Point start, Point end, bool IsIgnoreCorner){OpenList.Add(start);while (OpenList.Count != 0){//找出F值最小的點var tempStart = OpenList.MinPoint();OpenList.RemoveAt(0);CloseList.Add(tempStart);//找出它相鄰的點var surroundPoints = SurrroundPoints(tempStart, IsIgnoreCorner);foreach (Point point in surroundPoints){if (OpenList.Exists(point))//計算G值, 如果比原來的大, 就什么都不做, 否則設置它的父節點為當前點,并更新G和FFoundPoint(tempStart, point);else//如果它們不在開始列表里, 就加入, 并設置父節點,并計算GHFNotFoundPoint(tempStart, end, point);}if (OpenList.Get(end) != null)return OpenList.Get(end);}return OpenList.Get(end);}private void FoundPoint(Point tempStart, Point point){var G = CalcG(tempStart, point);if (G < point.G){point.ParentPoint = tempStart;point.G = G;point.CalcF();}}private void NotFoundPoint(Point tempStart, Point end, Point point){point.ParentPoint = tempStart;point.G = CalcG(tempStart, point);point.H = CalcH(end, point);point.CalcF();OpenList.Add(point);}private int CalcG(Point start, Point point){int G = (Math.Abs(point.X - start.X) + Math.Abs(point.Y - start.Y)) == 2 ? STEP : OBLIQUE;int parentG = point.ParentPoint != null ? point.ParentPoint.G : 0;return G + parentG;}private int CalcH(Point end, Point point){int step = Math.Abs(point.X - end.X) + Math.Abs(point.Y - end.Y);return step * STEP;}//獲取某個點周圍可以到達的點public List<Point> SurrroundPoints(Point point, bool IsIgnoreCorner){var surroundPoints = new List<Point>(9);for(int x = point.X -1; x <= point.X+1;x++)for (int y = point.Y - 1; y <= point.Y + 1; y++){if (CanReach(point,x, y,IsIgnoreCorner))surroundPoints.Add(x, y);}return surroundPoints;}//在二維數組對應的位置不為障礙物private bool CanReach(int x, int y){return MazeArray[x, y] == 0;}public bool CanReach(Point start, int x, int y, bool IsIgnoreCorner){if (!CanReach(x, y) || CloseList.Exists(x, y))return false;else{if (Math.Abs(x - start.X) + Math.Abs(y - start.Y) == 1)return true;//如果是斜方向移動, 判斷是否 "拌腳"else{if (CanReach(Math.Abs(x - 1), y) && CanReach(x, Math.Abs(y - 1)))return true;elsereturn IsIgnoreCorner;}}}}//Point 類型public class Point{public Point ParentPoint { get; set; }public int F { get; set; }  //F=G+Hpublic int G { get; set; }public int H { get; set; }public int X { get; set; }public int Y { get; set; }public Point(int x, int y){this.X = x;this.Y = y;}public void CalcF(){this.F = this.G + this.H;}}//對 List<Point> 的一些擴展方法public static class ListHelper{public static bool Exists(this List<Point> points, Point point){foreach (Point p in points)if ((p.X == point.X) && (p.Y == point.Y))return true;return false;}public static bool Exists(this List<Point> points, int x, int y){foreach (Point p in points)if ((p.X == x) && (p.Y == y))return true;return false;}public static Point MinPoint(this List<Point> points){points = points.OrderBy(p => p.F).ToList();return points[0];}public static void Add(this List<Point> points, int x, int y){Point point = new Point(x, y);points.Add(point);}public static Point Get(this List<Point> points, Point point){foreach (Point p in points)if ((p.X == point.X) && (p.Y == point.Y))return p;return null;}public static void Remove(this List<Point> points, int x, int y){foreach (Point point in points){if (point.X == x && point.Y == y)points.Remove(point);}}}
}

program.cs

using System;namespace Maze
{class Program{static void Main(string[] args){int[,] array = {{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},{ 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1},{ 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1},{ 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1},{ 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1},{ 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1},{ 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1},{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}};Maze maze = new Maze(array);Point start = new Point(1, 1);Point end = new Point(6, 10);var parent = maze.FindPath(start, end, false);Console.WriteLine("Print path:");while (parent != null){Console.WriteLine(parent.X + ", " + parent.Y);parent = parent.ParentPoint;}}}
}