近期題目來自校賽,賽前訓練,省賽熱身,河北ccpc正式比賽。
題目一:
題目描述:
由于第m個臺階上有好吃的薯條,所以薯片現在要爬一段m階的樓梯.
薯片每步最多能爬k個階梯,但是每到了第i個臺階,薯片身上的糖果都會掉落ai個,現在問你薯片至少得掉多少糖果才能得到薯條?
輸入:
多組數據輸入,每組數據第一行輸入兩個數字m(1<m<=1000),k(1<=k<m),接下來有m行,每一行輸入ai(0<ai<=1000),表示第i個臺階會掉落的糖果.
輸出:
對于每組數據,輸出至少要犧牲的糖果數.
樣例輸入
5 2
1 2 3 4 5
6 2
6 5 4 3 2 1
樣例輸出
9
9
分析:經過的數字全部加起來,為一個累加和,求最小累加和
遞推關系:
定義f(n)為必須到第n個臺階的最少累加和
分析可以如何得到f(n),我們通過跳一步,可以怎么跳到第n個臺階呢?
可以從第n-1個臺階跳到這里,可以n-2,n-3......n-k。
也就是說,
f(n)=an+min(f(n-1),f(n-2),......f(n-k))
必須到第n個臺階的最少累加和,就等于能跳到這里的所有位置中,最小的那個f(),跳過來(也就是加上本身)。
注意:前k個臺階可以從起點直接跳過來,貪心思想,經過任何多余的數字都不會是最優解。所以前k個f(n)直接賦值an.
也可以維持單調隊列把時間降到線性,不過o(n*k)已經足夠過了。
?
題目二:
題目描述:
JiangYu的小金庫是一個三維立體的空間,大小為XYZ,里面每個位置都藏著各種價值的寶物,既然是寶物價值自然非同一般,可正可負。
可惡的花花得知了這一切,想要偷走其中的珍寶們。
可是Jiangyu的小金庫安保措施十分嚴密,花花只有一次行動的機會,他決定偷走一個價值盡可能大的長方體區間。
那么他最大能偷走多少錢的寶物呢?
輸入:
第一行給出三個正整數 X,Y,Z
第二行一個整數n, 寶藏的數量
接下來n行,每行給出一個寶藏的位置xi,yi,zi, 以及價值ci
保證寶藏位置不重復。 (1 \leq X,Y,Z \leq 201≤X,Y,Z≤20)
(1 \leq n \leq X \times Y \times Z1≤n≤X×Y×Z)
(1 \leq xi \leq X1≤xi≤X)
(1 \leq yi \leq Y1≤yi≤Y)
(1 \leq zi \leq Z1≤zi≤Z)
(-1e9 \leq ci \leq 1e9?1e9≤ci≤1e9)
輸出:
一個整數,最大的價值
樣例輸入
2 2 2
8
1 1 1 10
1 1 2 9
1 2 1 10
1 2 2 9
2 1 1 10
2 1 2 9
2 2 1 -1
2 2 2 10
樣例輸出
66
?
https://blog.csdn.net/hebtu666/article/details/82788866這個網址寫了詳細講解哦。。。最好要看看
首先要明白一維最大子數組問題,設dp[n]的含義為必須以an結尾的數組中的最大和。
所以dp[n]就是,每一個以在n前面的結尾的最大值,加上an.
二維方法:轉化為一維來做。枚舉長度為原矩陣長度的所有矩陣。然后壓成一維來做。
時間:
因為有n個開頭,每個開頭有n-1,n-2......1個結尾,所以枚舉的時間復雜度為o(n^2)。
為了節省時間,利用預處理數組思想,定義長寬和原矩陣一樣的矩陣gg。
每列滿足第n列k行的值為sum(l[0][n]+l[1][n]....l[k][n]),可以o(n*m)做到(nm為長寬).然后枚舉到某矩陣的時候直接根據gg得出。整體做到o(n^2)枚舉并求和。然后按一維做。整體o(n^3)
三維:并沒有什么高大上的優化,也是枚舉每一個長寬固定的長方體,壓縮至二維,然后按二維做。
?
題目三:
熱身賽,并沒有原題,手打。
過的隊伍不多
一種動物,出生到死亡只有三年,即n年出生,n+3年死去。
出生一年以后可以生育,也就是n+1年開始生育,一年可以生一只寶寶。
定義第n年動物總數為an,給定n,返回an/a(n-1),最多保存小數點后十位
第一年有一只
思路一:定義f(n)為第n年新出生的動物個數,則f(n)=f(n-1)+f(n-2),前兩項為1,而每年的總數也就是三項求和而已。
每年出生的數量為1,1,2,3,5,8,13,21
每年總數就是1,2,4,10,16,26,42
發現是斐波那契數列
思路二:直接從總數入手,定義f(n)為第n年的總數
如何求出an/a(n-1):要看有多少動物能活到n年,活不到n年的也不能在第n年生育,活到n年的動物每人生一個,所以an就是二倍的能活到n年的動物。求此數方法很多,在此只說一個:
f(n-1)-(1/2)f(n-3)
去年的數量減去,去年還活著的今年就死了的數量。
這個數乘二,得出答案f(n)=2f(n-1)-f(n-3),其實本質還是斐波那契,因為f(n-1)=f(n-2)+f(n-3),帶入以后發現f(n)=f(n-1)+f(n-2)。
式子寫出來了,但是原題數據范圍是10^1000,不能一項一項推過去。
嘗試發現,幾十項之后,an/a(n-1)的十位小數之內都沒有變過,所以當數字較大時直接輸出第五十項即可。
本題結束
但是還有點別的東西想寫
?
斐波那契的美
萬物之美,總能找到斐波那契數列的規律。隨著n的增加,an/a(n-1)越來越接近黃金分割
手寫了求解過程。可能寫的不規范,但是就是表達這個意思。
?
只要數列滿足X(n) = X(n-1) + X(n-2),無論前兩個值是多少,都滿足黃金分割的條件,而斐波那契數列是最簡單的特例:前兩個元素均為1
數學家還發現了費馬大定理和這個數列的關系(費馬大定理的證明,三百五十年),并應用到諸多領域(比如加密)。有興趣自行了解。
?
題目四:
省賽,沒有原題。十六支隊伍過了這個題。
https://blog.csdn.net/hebtu666/article/details/79964233
參考我前面的文章,dp入門篇,那個會了這個就會。
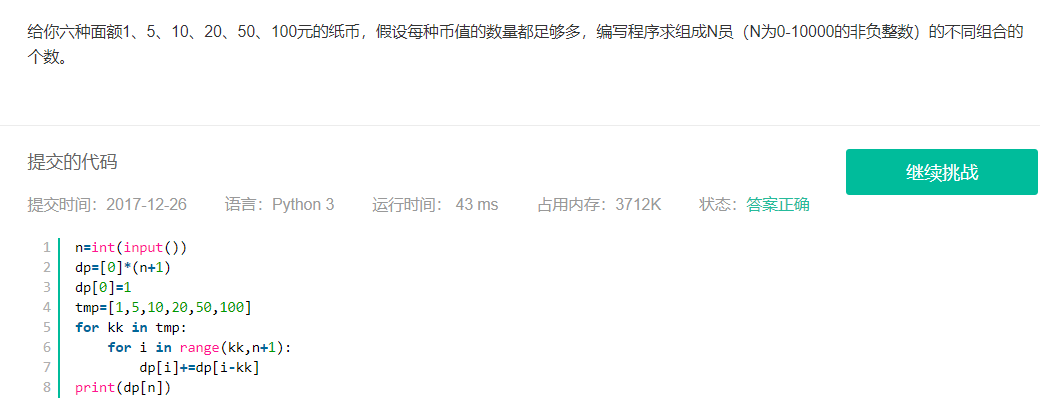
參考萌新題
現場因為對c++不熟,沒敢壓空間,規規矩矩的寫了一遍,還因為多打了一行罰了時,跟智障一樣。。。
?
?
題目五
http://newoj.acmclub.cn/contests/1359/problem/6
題意:最長公共子序列,要求序列每個元素重復k次,比如1122重復兩次,111222重復三次。
輸入兩個字符串和k,輸出長度。
最長公共子序列的一個變形。。。
動態規劃。設dp[i][j]表示a串處理到i位置,b串處理到j位置的答案。預處理出從a串i位置向前數,第k個與i位置數
字相同的位置p[i],用相同方式處理出B串的q[i]。
則轉移方程為dp[i][j]=max(dp[i-1][j],dp[i][j-1],dp[i-p[i]][j-q[j]]+1),其中第三種轉移必須在a[i]=b[j]的情況下轉移。
?
#include <bits/stdc++.h>
using namespace std;
int k,n,m,dp[1005][1005];
int a[1005],b[1005];
int pa[1005]={0},pb[1005]={0};
queue<int> q[1005];
int main()
{int ak; cin>>ak;while(ak--){for(int i=1;i<=n;i++)while(!q[i].empty()) q[i].pop();scanf("%d%d%d",&k,&n,&m);memset(dp,0,sizeof(dp));memset(pa,0,sizeof(pa));memset(pb,0,sizeof(pb));for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=m;i++) cin>>b[i];for(int i=1;i<=n;i++){q[a[i]].push(i);if(q[a[i]].size()==k){pa[i]=q[a[i]].front();q[a[i]].pop();}}for(int i=1;i<=n;i++)while(!q[i].empty()) q[i].pop();for(int i=1;i<=m;i++){q[b[i]].push(i);if(q[b[i]].size()==k){pb[i]=q[b[i]].front();q[b[i]].pop();}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dp[i][j]=max(dp[i-1][j],dp[i][j-1]);if(a[i]==b[j] && pa[i]!=0 && pb[j]!=0)dp[i][j]=dp[pa[i]-1][pb[j]-1]+k;}}printf("%d\n",dp[n][m]);}return 0;
}代碼都是比賽時候寫的,真的不想找來貼了。
?
最后總結經驗教訓:
?
注意細節,注意細節,注意細節
多種思路,多種思路,多種思路
遞歸關系自己推,比如背包,你要是看套路。。。Emmm。。就連套路都不會用了。
平時遞歸關系自己推,自己推,自己推。
?
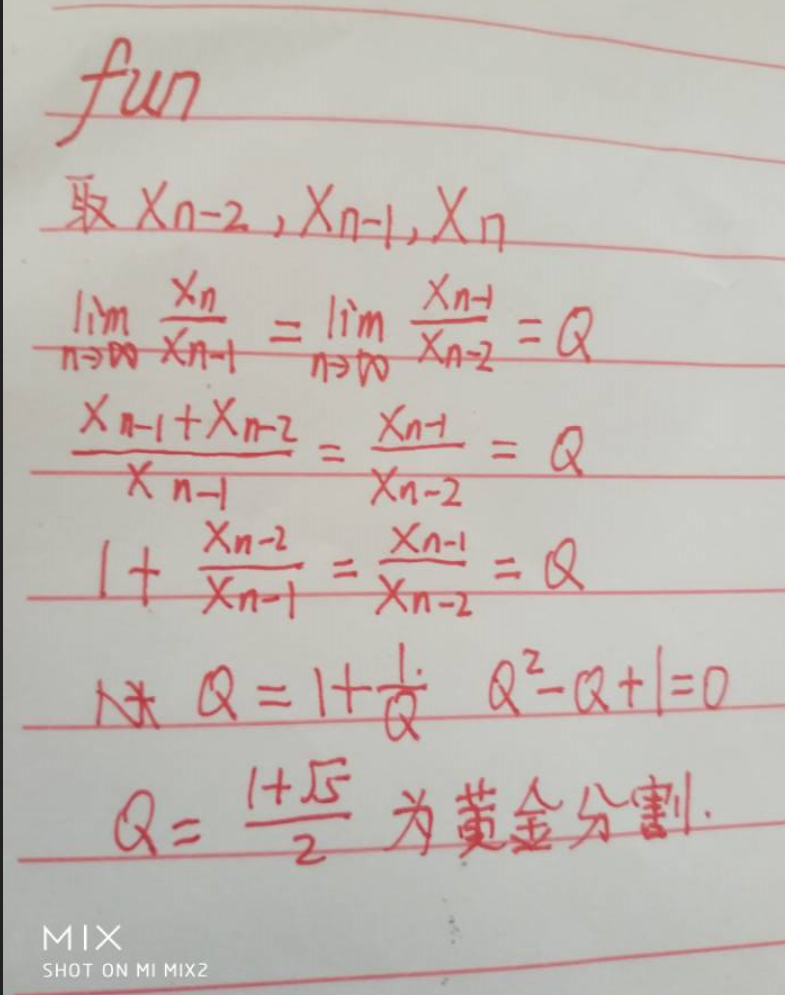




)


)
)


)


)

)
)
)
)