隨機過程1
- 概述
- 1.參考書目
- 2.主要內容
- 3.概率論--基本概念回顧
- 3.1對“不確定性”的認識
- 3.2 應對“不確定性”應該怎么做
- 3.3隨機變量(Random Variable)
- 3.4分布函數(Distribution Function)
- 3.5概率密度(Density)
- 3.6概率(Probability)
- 4.隨機過程
- 4.1 聯合分布
- 4.2分布密度--觀察兩個變量之間的關聯
- 4.3 兩種方法定性分析X,Y之間的關系
- 5.總結
概述
本系列文章計劃總結整理中國科學院大學《隨機過程》課程相關知識,課程主講老師:張顥
1.參考書目
- 《隨機過程及其應用》–陸大金 張顥 ;
- 《Probability Random Variables and Stochastic Process》–Dapoulis,4th Edition;
- 《Stochastic Process》–S.Ross,2ed Edition ;
- 《Introduction to Stachastic Models》,7th Edition ;
2.主要內容
隨機過程主要研究:多個隨機變量之間的關聯關系。關聯關系有:
關聯關系={LinearRelationship(Correlation)線性關系主要研究工具:相關Markovproperty研究連續和離散Martingale鞅,隨機過程在金融中的應用(選講)關聯關系=\left\{ \begin{aligned} Linear Relationship(Correlation) &&線性關系 主要研究工具:相關 \\ Markov property && 研究連續和離散 \\ Martingale && 鞅,隨機過程在金融中的應用(選講) \end{aligned} \right. 關聯關系=??????LinearRelationship(Correlation)MarkovpropertyMartingale??線性關系主要研究工具:相關研究連續和離散鞅,隨機過程在金融中的應用(選講)?
3.概率論–基本概念回顧
概率論主要研究:隨機性/不確定性(Randomness<=>Uncertainty)。
3.1對“不確定性”的認識
對于一般人來說“某次拋硬幣的結果”是不確定的。但是,如果一個人熟練的掌握拋硬幣整個過程的物理特性,如“拋時的用力“,”空氣動力學”等知識;那么他在硬幣起拋后對結果是確定的。愛因斯坦曾經說過:“引入不確定性是對無知的妥協”。那么,我們該如何正確看待不確定性呢?對于一般人而言,必須明確區分<有沒有必要/有沒有能力 知道不確定性>。
3.2 應對“不確定性”應該怎么做
設計統計實驗,統計實驗事先不知道實驗結果,一次實驗會產生一個結果;將所有可能的結果放在一起,構成樣本空間;研究每個統計結果可能出現的概率。
StatisticalExperiment<=>SampleSpace(Ω)<=>Probability(Possibility)Statistical Experiment<=>Sample Space(\Omega)<=>Probability(Possibility) StatisticalExperiment<=>SampleSpace(Ω)<=>Probability(Possibility)
概率的重要特性:可數可加性
3.3隨機變量(Random Variable)
隨機變量是一個函數,具有確定的形式;是由樣本空間->函數值的一個確定的映射。隨機變量本身沒有隨機性,具有隨機性的是:樣本空間中的樣本點。隨機變量的作用是:對樣本空間中的樣本點起量化作用。因為,統計實驗的結果沒有數值意義。如拋硬幣實驗的結果是“正”、”負“,需要將結果進行數值化后,才能夠進行數學計算。
X:Ω?>R(Determined)X:\Omega->R(Determined) X:Ω?>R(Determined)
3.4分布函數(Distribution Function)
FX=P(X≤x)=P({ω:X(ω)≤x})F_X=P(X\leq x)=P(\{\omega:X(\omega)\leq x\}) FX?=P(X≤x)=P({ω:X(ω)≤x})
3.5概率密度(Density)
概率密度函數為分布函數的導數,概率密度函數的兩個特性:恒大于零、積分為1.
fX(x)=ddxFX(x)f_X(x)=\frac{d}{dx} F_X(x) fX?(x)=dxd?FX?(x)
3.6概率(Probability)
P(A)=∑x∈AP({x})P(A)= \sum_{x \in A} P(\{ x\}) P(A)=x∈A∑?P({x})
P(A)=∫AfX(x)dxP(A)= \int_A f_X(x)dx P(A)=∫A?fX?(x)dx
4.隨機過程
研究多個隨機變量之間的關系,以下以兩個隨機變量X,Y為例,簡單說明。
4.1 聯合分布
X,Y兩個隨機變量,基于同一個樣本空間,研究兩個隨機變量的取值之間的相互影響程度。
X,Y:Ω?>RX,Y:\Omega->R X,Y:Ω?>R
P(X=x,Y=y)=Pxy=P({ω:X(ω)=x}∩{ω:Y(ω)=y})P(X=x,Y=y)=P_{xy}=P(\{\omega :X(\omega)=x\} \cap \{\omega :Y(\omega)=y\}) P(X=x,Y=y)=Pxy?=P({ω:X(ω)=x}∩{ω:Y(ω)=y})
4.2分布密度–觀察兩個變量之間的關聯
二元函數的分布函數為聯合函數的混合偏導數。分布函數形式確定了兩個隨機變量之間的取值影響關系,下面展示三個簡單的例子。
例子1
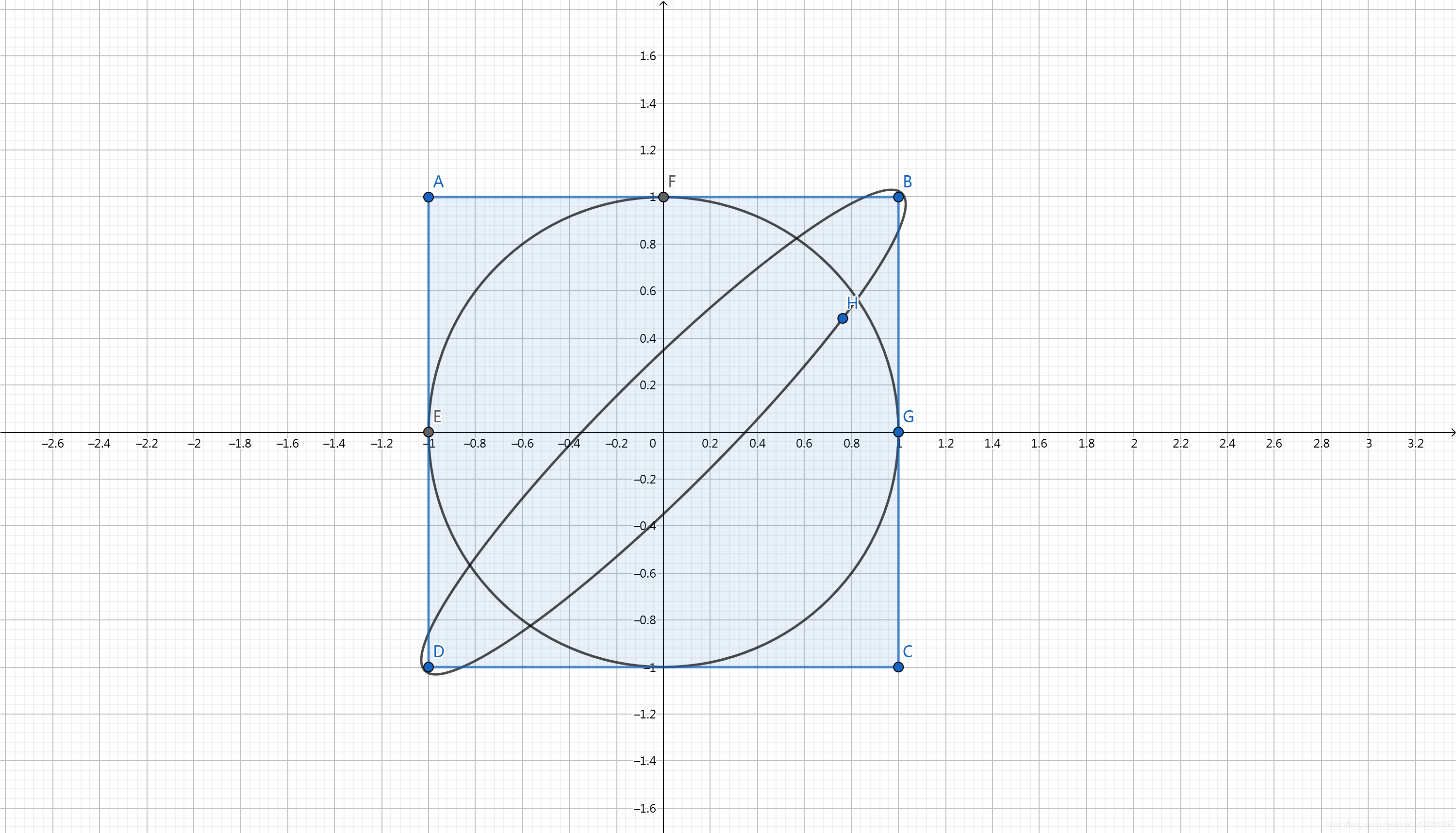
fXY(x,y)={14∣x∣≤1,∣y∣≤10otherwisef_{XY}(x,y)=\left\{ \begin{aligned} \frac{1}{4} &&|x|\leq1, |y|\leq 1\\ 0 && otherwise \\ \end{aligned} \right. fXY?(x,y)=????41?0??∣x∣≤1,∣y∣≤1otherwise?


X在(-1,1) 之間任取一個確定的值時,Y的取值范圍都是(-1,1);所以,不難看出X的取值不影響Y的取值。即兩個隨機變量之間沒有任何關聯。
例子2
fXY(x,y)={1πx2+y2≤10otherwisef_{XY}(x,y)=\left\{ \begin{aligned} \frac{1}{\pi} &&x^2+y^2\leq1\\ 0 && otherwise \\ \end{aligned} \right. fXY?(x,y)=????π1?0??x2+y2≤1otherwise?

X在(-1,1) 之間取一個確定的值時,Y的取值范是在變化的;所以,不難看出X的取值會影響Y的取值。即兩個隨機變量之間有某種關系。
例子3
下例不考慮概率密度的嚴格形式,圖為概率等高線投影圖。直觀看來,此時X,Y之間的關系近似于線性。

三個例子小結:
概率密度投影(方->圓->橢圓),隨機變量X,Y之間的關系趨向于線性。那么兩者之間的關系可否寫出例如y=αxy=\alpha xy=αx的形式?
y=αx=>Y?=αX(Y(ω)?=αX(ω))y=\alpha x=>Y?=\alpha X(Y(\omega)?=\alpha X(\omega)) y=αx=>Y?=αX(Y(ω)?=αX(ω))
有兩種方法來研究此關系式。
4.3 兩種方法定性分析X,Y之間的關系
4.3.1方法1:
步驟1: Metric 明確度量
步驟2: Optimization 優化
要考慮上述關系式子是否成立,首先要考慮”=“是否成立;其次比例系數α\alphaα是多少。用d(Y,αX)d(Y,\alpha X)d(Y,αX)表示Y,αXY,\alpha XY,αX之間的距離,則目標是將此距離控制在盡可能小的范圍內。如果采用均方距離,目標函數為:
min?α(d(Y,αX))=min?α(E∣Y?αX∣2)\min_{\alpha}(d(Y,\alpha X))=\min_{\alpha}(E|Y-\alpha X|^2) αmin?(d(Y,αX))=αmin?(E∣Y?αX∣2)
g(α)=E∣Y?αX∣2g(\alpha)=E|Y-\alpha X|^2 g(α)=E∣Y?αX∣2
▽αg(α)=▽α(E∣Y∣2+α2E∣X∣2?2αE∣XY∣)=2αE∣X∣2?2E∣XY∣=0\bigtriangledown _\alpha g(\alpha)=\bigtriangledown _\alpha(E|Y|^2+\alpha ^2E|X|^2-2\alpha E|XY|)=2\alpha E|X|^2-2E|XY|=0 ▽α?g(α)=▽α?(E∣Y∣2+α2E∣X∣2?2αE∣XY∣)=2αE∣X∣2?2E∣XY∣=0
=>α=E∣XY∣E∣X∣2=>\alpha =\frac{E|XY|}{E|X|^2} =>α=E∣X∣2E∣XY∣?
α\alphaα中的E(XY)表征了 隨機變量XY之間的相關關系,E(XY)為二元函數H?H?>RH*H->RH?H?>R,具有:非負、對稱、雙線性三個性質(三個性質的展示缺失)。與此同時,以上三個性質符合內積的定義。所以E(XY)的幾何含義為:
E(XY)=<X,Y>E(XY)=<X,Y> E(XY)=<X,Y>
仿照兩向量間夾角公式:
cos?∠(x,y)=<x,y><x,x><y,y>=xTy∣∣x∣∣2∣∣y∣∣2\cos \angle(x,y)=\frac{<x,y>}{<x,x><y,y>}=\frac{x^Ty}{||x||_2||y||_2} cos∠(x,y)=<x,x><y,y><x,y>?=∣∣x∣∣2?∣∣y∣∣2?xTy?
cos?∠(X,Y)=E(XY)E∣X∣2E∣Y∣2(CorrelationCoefficient)\cos \angle(X,Y)=\frac{E(XY)}{\sqrt{ E|X|^2E|Y|^2}}(Correlation Coefficient) cos∠(X,Y)=E∣X∣2E∣Y∣2?E(XY)?(CorrelationCoefficient)
如果E(XY)=0
=>cos?∠(X,Y)=π2=>Orthogonality=>\cos \angle(X,Y)=\frac{\pi}{2}=>Orthogonality =>cos∠(X,Y)=2π?=>Orthogonality
4.3.2 方法2
從幾何的角度解釋X,Y之間的關系:
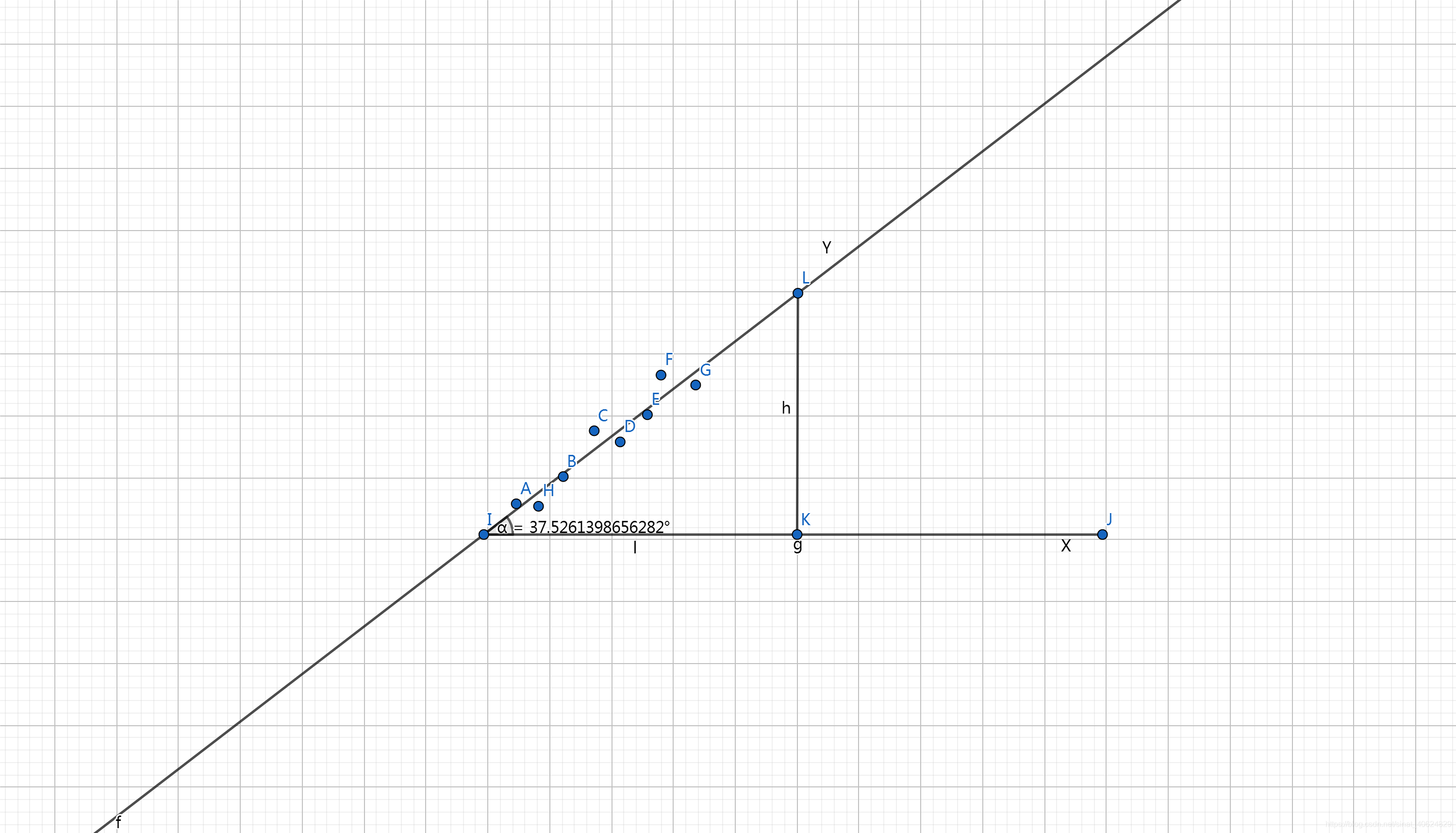
變量Y擬合直線在水平坐標軸上的投影為:
l=∣∣Y∣∣cosα=∣∣Y∣∣<X,Y>∣∣X∣∣∣∣Y∣∣=<X,Y>∣∣X∣∣l=||Y||cos\alpha=||Y||\frac{<X,Y>}{||X||||Y||}=\frac{<X,Y>}{||X||} l=∣∣Y∣∣cosα=∣∣Y∣∣∣∣X∣∣∣∣Y∣∣<X,Y>?=∣∣X∣∣<X,Y>?
l?=lX∣∣X∣∣=<X,Y>∣∣X∣∣X∣∣X∣∣=<X,Y>∣∣X∣∣2X=E(X,Y)E∣X∣2X\vec l=l\frac{X}{||X||}=\frac{<X,Y>}{||X||}\frac{X}{||X||}=\frac{<X,Y>}{||X||^2}X=\frac{E(X,Y)}{E|X|^2}X l=l∣∣X∣∣X?=∣∣X∣∣<X,Y>?∣∣X∣∣X?=∣∣X∣∣2<X,Y>?X=E∣X∣2E(X,Y)?X
5.總結
隨機過程主要研究多個隨機變量之間關系,通過各種方法表示這些關系。此文對隨機過程的實際應用討論缺失,希望能在此后的文章中填補此塊空白。(6h)
)
)
-touch,mkdir,rm,mv,cp,ls,cd,cat)
)
-大數據知識框圖)

)
-大數據概述)
)

)

-概述)
-Hadoop的介紹與安裝)


-Hadoop安裝教程-單機模式和偽分布模式(Ubuntu14.04LTS))


)