文章目錄

哈希
哈希（散列）函數
- 常見的哈希函數
- 字符串哈希函數
哈希沖突
- 閉散列（開放地址法）
- 開散列（鏈地址法/拉鏈法）
- 負載因子以及增容
- - 對于閉散列
- 對于開散列結構
具體實現
- 哈希表（閉散列）
- - 創建
  - 插入
  - 查找
  - 刪除
  - 完整代碼
- 哈希桶（開散列）
- - 插入
  - 查找
  - 刪除
  - 完整代碼

哈希

哈希（散列）是一種數據結構，通過散列算法將元素值轉換為散列值進行存儲。使得元素存儲的位置與元素本身建立起了映射關系，如果要查、改數據，就可以直接到對應的位置去，使得時間復雜度達到了 O(1) ，原因如下：

若結構中存在和 關鍵字K 相等的記錄，則必定在 f(K) 的存儲位置上。由此，不需比較便可直接取得所查記錄。

稱上面的對應關系 f 為 散列函數（Hash function），按這個映射關系事先建立的表為散列表，這一映象過程稱為 散列造表 或散列，最終所得的存儲位置稱 散列地址 。

哈希（散列）函數

哈希函數用來建立元素與其存儲位置的映射關系。

對于哈希函數來說，必須具有以下特點：

哈希函數的定義域必須包括需要存儲的全部關鍵碼，而如果散列表允許有 m 個地址時，其值域必須在 0 到 m-1 之間。
哈希函數計算出來的地址能均勻分布在整個空間中（防止產生密集的哈希沖突）

哈希沖突大量出現往往都是因為哈希函數設計的不夠合理，但是即使再優秀的哈希函數，也只能盡量減少哈希沖突的次數，無法避免哈希沖突。

常見的哈希函數

直接定址法（常見）
哈希函數：Hash(Key) = A * Key + B
這是最簡單的哈希函數，直接取關鍵字本身或者他的線性函數來作為散列地址。
除留余數法（常見）
哈希函數：Hash(key) = key % capacity
幾乎是最常用的哈希函數，用一個數來對 key 取模，一般來說這個數都是容量。
平方取中法
對關鍵字進行平方，然后取中間的幾位來作為地址。
折疊法
折疊法是將關鍵字從左到右分割成位數相等的幾部分（最后一部分位數可以短些），然后將這幾部分疊加求和（去除進位），并按散列表表長，取后幾位作為散列地址。
折疊法適合事先不需要知道關鍵字的分布，適合關鍵字位數比較多的情況.
隨機數法
選擇一個隨機函數，取關鍵字的隨機函數值為它的哈希地址，即 H(key) = random(key)，其中 random 為隨機數函數。通常應用于關鍵字長度不等時。
數學分析法
分析一組數據，比如一組員工的出生年月日，這時我們發現出生年月日的前幾位數字大體相同，這樣的話，出現沖突的幾率就會很大，但是我們發現年月日的后幾位表示月份和具體日期的數字差別很大，如果用后面的數字來構成散列地址，則沖突的幾率會明顯降低。因此數字分析法就是找出數字的規律，盡可能利用這些數據來構造沖突幾率較低的散列地址。

字符串哈希函數

因為哈希函數的常用方法如直接定址、除留余數、平方取中等方法需要用的 key值 為整型，而大部分時候我們的 key 都是 string，由于無法對 string 進行算數運算，所以需要考慮新的方法。

常見的字符串哈希算法有 BKD、SDB、RS 等，這些算法大多通過一些公式來對字符串每一個 字符的 ascii值 或者 字符串的大小 進行計算，來推導出一個不容易產生沖突的 key值 。

例如 BKDHash ：

struct _Hash<std::string>
{const size_t& operator()(const std::string& key){// BKDR字符串哈希函數size_t hash = 0;for (size_t i = 0; i < key.size(); i++){hash *= 131;hash += key[i];}return hash;}
};

這里推薦兩篇文章，一篇具體對比各類字符串哈希函數的效率，一篇是實現：

字符串Hash函數對比
各種字符串Hash函數

哈希沖突

對不同的關鍵字可能得到同一散列地址，即 key1≠key2 ，而 f(key1)=f(key2) ，這種現象稱碰撞（哈希沖突）。

哈希沖突使得多個數據映射的位置相同，但是每個位置又只能存儲一個數據，所以就需要通過某種方法來解決哈希沖突。

查找過程中，關鍵碼的比較次數，取決于產生沖突的多少，產生的沖突少，查找效率就高；產生的沖突多，查找效率就低。因此，影響產生沖突多少的因素，也就是影響查找效率的因素。影響產生沖突多少有以下三個因素：

散列函數是否均勻；
處理沖突的方法；
散列表的負載因子（裝填因子）。

第一點取決于上面講過的哈希函數，不再贅述，下面詳細講一下2、3點。

處理沖突的方法可分為兩類：開散列方法( open hashing，也稱為拉鏈法，separate chaining ) 和 閉散列方法( closed hashing，也稱為開地址方法，open addressing )。這兩種方法的不同之處在于：開散列法把發生沖突的關鍵碼存儲在散列表主表之外，而閉散列法把發生沖突的關鍵碼存儲在表中另一個槽內。

閉散列（開放地址法）

因為閉散列是順序的結構，所以可以通過遍歷哈希表，來將沖突的數據放到空的位置上。

線性探測
線性探測即為從發生沖突的位置開始，依次向后探測，直到尋找到下一個空位置為止。
這種方法實現起來極為簡單，但是效率也不高，因為如果同一位置產生了大量的哈希沖突，就會導致每次都在同一個位置進行探測，例如我在10這里連續沖突100次，此時所有探測的次數加起來就會高達100！
二次探測
二次探測即為從發生沖突的位置開始，每次往后探測 ±k²(k<=m/2，m為散列表長) 個位置，如：1²，-(1²)，2²，-(2²) 等。
這樣的話就將每次探測的效率從 O(N) 提升到了 O(logN) ，即使有著大量的沖突堆積，也不會導致效率過低。
偽隨機數探測
這種方法并不常見，實現方法是：創建一個偽隨機數序列，根據序列內容決定每次往后探測的長度。

開散列（鏈地址法/拉鏈法）

先用哈希函數計算每個數據的散列地址，把具有相同地址的元素歸于同一個集合之中，把該集合處理為一個鏈表，鏈表的頭節點存儲于哈希表之中。

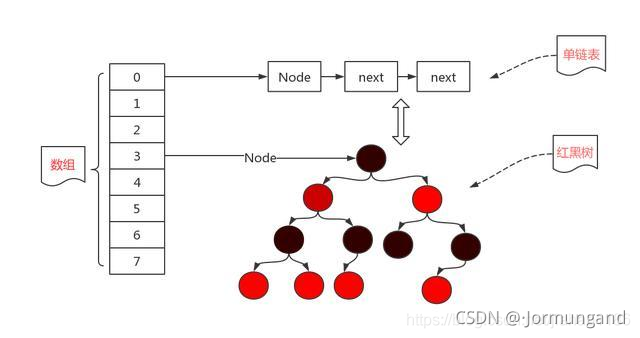
在這里插入圖片描述

鏈地址法在每一個映射位置都建立起一個鏈表（數據過多時可能會轉為建立紅黑樹），將每次插入的數據都直接連接上這個鏈表，這樣就不會像閉散列一樣進行大量的探測，但是如果鏈表過長也會導致效率低下。

負載因子以及增容

哈希沖突出現的較為密集，往往代表著此時數據過多，而能夠映射的地址過少，而要想解決這個問題，就需要通過 負載因子（裝填因子） 的判斷來進行增容。

負載因子的大小 = 表中數據個數 / 表的容量（長度）

對于閉散列

對于閉散列來說，因為其是一種線性的結構，所以一旦負載因子過高，就很容易出現哈希沖突的堆積，所以當負載因子達到一定程度時就需要進行增容，并且增容后，為了保證映射關系，還需要將數據重新映射到新位置。

經過算法科學家的計算，負載因子應當嚴格的控制在 0.7-0.8 以下，所以一旦負載因子到達這個范圍，就需要進行增容。

因為除留余數法等方法通常是按照表的容量來計算，所以科學家的計算，當對一個質數取模時，沖突的幾率會大大的降低，并且因為增容的區間一般是 1.5-2 倍，所以算法科學家列出了一個增容質數表，按照這樣的規律增容，沖突的幾率會大大的降低。

這也是 STL 中 unordered_map/unordered_set 使用的增容方法。

//算法科學家總結出的一個增容質數表，按照這樣增容的效率更高const int PRIMECOUNT = 28;const size_t primeList[PRIMECOUNT] = {53ul, 97ul, 193ul, 389ul, 769ul,1543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul, 98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,1610612741ul, 3221225473ul, 4294967291ul};

hashmap 的負載因子為什么默認是 0.75 ？

比如說當前的容器容量是 16，負載因子是 0.75,16*0.75=12，也就是說，當容量達到了 12 的時候就會進行擴容操作。而負載因子定義為 0.75 的原因是：

當負載因子是 1.0 的時候，也就意味著，只有當散列地址全部填充了，才會發生擴容。意味著隨著數據增長，最后勢必會出現大量的沖突，底層的紅黑樹變得異常復雜。雖然空間利用率上去了，但是查詢時間效率降低了。
負載因子是 0.5 的時候，這也就意味著，當數組中的元素達到了一半就開始擴容。雖然時間效率提升了，但是空間利用率降低了。 誠然，填充的元素少了，Hash沖突也會減少，那么底層的鏈表長度或者是紅黑樹的高度就會降低。查詢效率就會增加。但是，這時候空間利用率就會大大的降低，原本存儲 1M 的數據，現在就意味著需要 2M 的空間。

對于開散列結構

因為哈希桶是開散列的鏈式結構，發生了哈希沖突是直接在對應位置位置進行頭插，而桶的個數是固定的，而插入的數據會不斷增多，隨著數據的增多，就可能會導致某一個桶過重，使得效率過低。

所以最理想的情況，就是每個桶都有一個數據。這種情況下，如果往任何一個地方插入，都會產生哈希沖突，所以當數據個數與桶的個數相同時，也就是負載因子為 1 時就需要進行擴容。

具體實現

哈希表（閉散列）

創建

對于閉散列，我們需要通過狀態來記錄一個數據是否在表中，所以這里會使用枚舉來實現。

enum State
{EMPTY,//空EXITS,//存在DELETE,//已經刪除
};template<class T>
struct HashData
{HashData(const T& data = T(), const State& state = EMPTY): _data(data), _state(state){}T _data;State _state;
};

插入

插入的思路很簡單，計算出映射的地址后，開始遍歷判斷下面幾種狀態：

如果映射位置已存在數據，并且值與當前數據不同，則說明產生沖突，繼續往后查找
如果映射位置的數據與插入的數據相同，則說明此時數據已經插入過，此時就不需要再次插入
如果映射位置的狀態為刪除或者空，則代表著此時表中沒有這個數據，在這個位置插入即可

bool Insert(const T& data)
{KeyOfT koft;//判斷此時是否需要增容//當裝填因子大于0.7時增容if (_size * 10 / _table.size() >= 7){//增容的大小按照別人算好的近似兩倍的素數來增，這樣效率更高，也可以直接2倍或者1.5倍。std::vector<HashData> newTable(getNextPrime(_size));for (size_t i = 0; i < _table.size(); i++){//將舊表中的數據全部重新映射到新表中if (_table[i]._state == EXITS){//如果產生沖突，則找到一個合適的位置size_t index = HashFunc(koft(_table[i]._data));while (newTable[i]._state == EXITS){i++;if (i == _table.size()){i = 0;}}newTable[i] = _table[i];}}//最后直接將數據進行交換即可，原來的數據會隨著函數棧幀一起銷毀_table.swap(newTable);}//用哈希函數計算出映射的位置size_t index = HashFunc(koft(data));//從那個位置開始探測, 如果該位置已經存在時，有兩種情況，一種是已經存在，一種是沖突，這里使用的是線性探測while (_table[index]._state == EXITS){//如果已經存在了，則說明不用插入if (koft(_table[index]._data) == koft(data)){return false;}else{index++;index = HashFunc(index);}}//如果走到這里，說明這個位置是空的或者已經被刪除的位置，可以在這里插入_table[index]._data = data;_table[index]._state = EXITS;_size++;return true;
}

查找

查找也分幾種情況

如果映射的位置為空，則說明查找失敗。
如果映射的位置的數據不同，則說明產生沖突，繼續向后查找
如果映射的位置的數據相同，如果狀態為刪除，則說明數據已經刪除，查找失敗；而如果數據為存在，則說明查找成功。

HashData* Find(const K& key)
{KeyOfT koft;size_t index = HashFunc(key);//遍歷，如果查找的位置為空，則說明查找失敗while (_table[index]._state != EMPTY){//此時判斷這個位置的數據是否相同，如果不同則說明出現哈希沖突，繼續往后查找if (koft(_table[index]._data) == key){//此時有兩個狀態，一種是數據已經被刪除，一種是數據存在。if (_table[index]._state == EXITS){return &_table[index];}else if (_table[index]._state == DELETE){return nullptr;}}index++;//如果index越界，則歸零if (index == _table.size()){index = 0;}}return nullptr;
}

刪除

直接遍歷查找數據，如果找不到則說明已經被刪除，如果找到了則直接將狀態改為刪除即可。

bool Erase(const K& key)
{HashData* del = Find(key);//如果找不到則說明已經被刪除if (del == nullptr){return false;}else{//找到了則直接更改狀態即可del->_state = DELETE;_size--;return true;}
}

完整代碼

#pragma once
#include<vector>namespace lee
{//算法科學家總結出的一個增容質數表，按照這樣增容的效率更高const int PRIMECOUNT = 28;const size_t primeList[PRIMECOUNT] = {53ul, 97ul, 193ul, 389ul, 769ul,1543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul, 98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,1610612741ul, 3221225473ul, 4294967291ul};enum State{EMPTY,EXITS,DELETE,};template<class T>struct HashData{HashData(const T& data = T(), const State& state = EMPTY): _data(data), _state(state){}T _data;State _state;};template<class K, class T, class KeyOfT>class HashTable{public:typedef HashData<T> HashData;HashTable(size_t capacity = 10): _table(capacity), _size(0){}size_t getNextPrime(size_t num){size_t i = 0;for (i = 0; i < PRIMECOUNT; i++){//返回比那個數大的下一個質數 if (primeList[i] > num){return primeList[i];}}//如果比所有都大，還是返回最后一個，因為最后一個已經是32位最大容量return primeList[PRIMECOUNT - 1];}//除留余數法size_t HashFunc(const K& key){return key % _table.size();}bool Insert(const T& data){KeyOfT koft;//判斷此時是否需要增容//當裝填因子大于0.7時增容if (_size * 10 / _table.size() >= 7){//增容的大小按照別人算好的近似兩倍的素數來增，這樣效率更高，也可以直接2倍或者1.5倍。std::vector<HashData> newTable(getNextPrime(_size));for (size_t i = 0; i < _table.size(); i++){//將舊表中的數據全部重新映射到新表中if (_table[i]._state == EXITS){//如果產生沖突，則找到一個合適的位置size_t index = HashFunc(koft(_table[i]._data));while (newTable[i]._state == EXITS){i++;if (i == _table.size()){i = 0;}}newTable[i] = _table[i];}}//最后直接將數據進行交換即可，原來的數據會隨著函數棧幀一起銷毀_table.swap(newTable);}//用哈希函數計算出映射的位置size_t index = HashFunc(koft(data));//從那個位置開始探測, 如果該位置已經存在時，有兩種情況，一種是已經存在，一種是沖突，這里使用的是線性探測while (_table[index]._state == EXITS){//如果已經存在了，則說明不用插入if (koft(_table[index]._data) == koft(data)){return false;}else{index++;index = HashFunc(index);}}//如果走到這里，說明這個位置是空的或者已經被刪除的位置，可以在這里插入_table[index]._data = data;_table[index]._state = EXITS;_size++;return true;}HashData* Find(const K& key){KeyOfT koft;size_t index = HashFunc(key);//遍歷，如果查找的位置為空，則說明查找失敗while (_table[index]._state != EMPTY){//此時判斷這個位置的數據是否相同，如果不同則說明出現哈希沖突，繼續往后查找if (koft(_table[index]._data) == key){//此時有兩個狀態，一種是數據已經被刪除，一種是數據存在。if (_table[index]._state == EXITS){return &_table[index];}else if (_table[index]._state == DELETE){return nullptr;}}index++;//如果index越界，則歸零if (index == _table.size()){index = 0;}}return nullptr;}bool Erase(const K& key){HashData* del = Find(key);//如果找不到則說明已經被刪除if (del == nullptr){return false;}else{//找到了則直接更改狀態即可del->_state = DELETE;_size--;return true;}}private:std::vector<HashData> _table;size_t _size;};
};

哈希桶（開散列）

開散列也叫哈希桶，桶為每一個映射的位置，桶一般用鏈表或者紅黑樹實現（這里我用的是鏈表）。當我們通過映射的地址，找到存放數據的桶，再對桶進行插入或者刪除操作即可。

插入

通過計算映射位置找到對應的桶，再判斷數據是否存在后將數據頭插進去即可（也可以尾插）

bool Insert(const T& data)
{KeyofT koft;/*因為哈希桶是開散列的鏈式結構，發生了哈希沖突是直接在對應位置位置進行頭插，而桶的個數是固定的，而插入的數據會不斷增多，隨著數據的增多，就可能會導致某一個桶過重，使得效率過低。所以最理想的情況，就是每個桶都有一個數據。這種情況下，如果往任何一個地方插入，都會產生哈希沖突，所以當數據個數與桶的個數相同時，也就是負載因子為1時就需要進行擴容。*/if (_size == _table.size()){//按照素數表來增容size_t newSize = getNextPrime(_table.size());size_t oldSize = _table.size();std::vector<Node*> newTable(newSize);_table.resize(newSize);//接著將數據重新映射過去for (size_t i = 0; i < oldSize; i++){Node* cur = _table[i];while (cur){//重新計算映射的位置size_t pos = HashFunc(koft(cur->_data));//找到位置后頭插進對應位置Node* next = cur->_next;cur->_next = newTable[pos];newTable[pos] = cur;cur = next;}//原數據置空_table[i] == nullptr;}//直接和新表交換，交換過去的舊表會和函數棧幀一塊銷毀。_table.swap(newTable);}size_t pos = HashFunc(koft(data));Node* cur = _table[pos];//因為哈希桶key值唯一，如果已經在桶中則返回falsewhile (cur){if (koft(cur->_data) == koft(data)){return false;}else{cur = cur->_next;}}//檢查完成，此時開始插入，這里選擇的是頭插，這樣就可以減少數據遍歷的次數。Node* newNode = new Node(data);newNode->_next = _table[pos];_table[pos] = newNode;++_size;return true;
}

查找

直接根據映射的位置到桶中查找數據即可

Node* Find(const K& key)
{KeyofT koft;size_t pos = HashFunc(key);Node* cur = _table[pos];while (cur){if (koft(cur->_data) == key){return cur;}else{cur = cur->_next;}}return nullptr;
}

刪除

bool Erase(const K& key)
{KeyofT koft;size_t pos = HashFunc(key);Node* cur = _table[pos];Node* prev = nullptr;while (cur){if (koft(cur->_data) == key){//如果要刪除的是第一個節點，就讓下一個節點成為新的頭節點，否則直接刪除。if (prev == nullptr){_table[pos] = cur->_next;}else{prev->_next = cur->_next;}delete cur;--_size;return true;}else{prev = cur;cur = cur->_next;}}return false;
}

完整代碼

#pragma once
#include<vector>
#include<string>namespace lee
{//算法科學家總結出的一個增容質數表，按照這樣增容的效率更高const int PRIMECOUNT = 28;const size_t primeList[PRIMECOUNT] = {53ul, 97ul, 193ul, 389ul, 769ul,1543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul, 98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,1610612741ul, 3221225473ul, 4294967291ul};/*因為哈希函數的常用方法如直接定地、除留余數、平方取中等方法需要用的key值為整型，而大部分時候我們的key都是string，或者某些自定義類型，這個時候就可以提供一個仿函數的接口給外部，讓他自己處理如何將key轉換成我們需要的整型*/template<class K>struct Hash{const K& operator()(const K& key){return key;}};template<>struct Hash<std::string>{const size_t & operator()(const std::string& key){//BKDR字符串哈希函數size_t hash = 0;for (size_t i = 0; i < key.size(); i++){hash *= 131;hash += key[i];}return hash;}};template<class T>struct HashNode{HashNode(const T& data = T()): _data(data), _next(nullptr){}T _data;HashNode<T>* _next;};template<class K, class T, class KeyofT, class Hash = Hash<K>>class HashBucket{public:typedef HashNode<T> Node;HashBucket(size_t capacity = 10): _table(capacity), _size(0){}~HashBucket(){Clear();}size_t getNextPrime(size_t num){size_t i = 0;for (i = 0; i < PRIMECOUNT; i++){//返回比那個數大的下一個質數 if (primeList[i] > num){return primeList[i];}}//如果比所有都大，還是返回最后一個，因為最后一個已經是32位最大容量return primeList[PRIMECOUNT - 1];}size_t HashFunc(const K& key){Hash hash;return hash(key) % _table.size();}bool Insert(const T& data){KeyofT koft;/*因為哈希桶是開散列的鏈式結構，發生了哈希沖突是直接在對應位置位置進行頭插，而桶的個數是固定的，而插入的數據會不斷增多，隨著數據的增多，就可能會導致某一個桶過重，使得效率過低。所以最理想的情況，就是每個桶都有一個數據。這種情況下，如果往任何一個地方插入，都會產生哈希沖突，所以當數據個數與桶的個數相同時，也就是負載因子為1時就需要進行擴容。*/if (_size == _table.size()){//按照素數表來增容size_t newSize = getNextPrime(_table.size());size_t oldSize = _table.size();std::vector<Node*> newTable(newSize);_table.resize(newSize);//接著將數據重新映射過去for (size_t i = 0; i < oldSize; i++){Node* cur = _table[i];while (cur){//重新計算映射的位置size_t pos = HashFunc(koft(cur->_data));//找到位置后頭插進對應位置Node* next = cur->_next;cur->_next = newTable[pos];newTable[pos] = cur;cur = next;}//原數據置空_table[i] == nullptr;}//直接和新表交換，交換過去的舊表會和函數棧幀一塊銷毀。_table.swap(newTable);}size_t pos = HashFunc(koft(data));Node* cur = _table[pos];//因為哈希桶key值唯一，如果已經在桶中則返回falsewhile (cur){if (koft(cur->_data) == koft(data)){return false;}else{cur = cur->_next;}}//檢查完成，此時開始插入，這里選擇的是頭插，這樣就可以減少數據遍歷的次數。Node* newNode = new Node(data);newNode->_next = _table[pos];_table[pos] = newNode;++_size;return true;}bool Erase(const K& key){KeyofT koft;size_t pos = HashFunc(key);Node* cur = _table[pos];Node* prev = nullptr;while (cur){if (koft(cur->_data) == key){//如果要刪除的是第一個節點，就讓下一個節點成為新的頭節點，否則直接刪除。if (prev == nullptr){_table[pos] = cur->_next;}else{prev->_next = cur->_next;}delete cur;--_size;return true;}else{prev = cur;cur = cur->_next;}}return false;}Node* Find(const K& key){KeyofT koft;size_t pos = HashFunc(key);Node* cur = _table[pos];while (cur){if (koft(cur->_data) == key){return cur;}else{cur = cur->_next;}}return nullptr;}void Clear(){//刪除所有節點for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_table[i] = nullptr;}}private:std::vector<Node*> _table;size_t _size;};
};