圖像理想低通濾波_圖像處理之濾波（下）

[toc]目錄

一、常規濾波

低通
高通
帶通
帶阻

二、非局部均值濾波

三、維納濾波

四、卡爾曼濾波

前言

所謂濾波，其實就是從混合在一起的諸多信號中提取出所需要的信號。

信號的分類：

確定型信號，可以表示為確定的時間函數，可確定其在任何時刻的量值。（具有確定的頻譜）；一般可通過低通、高通、帶通、帶阻等模擬濾波器或其他常規濾波算法實現。
隨機信號，不能用確定的數學關系式描述，不能預測其未來任何瞬時值，其值的變化服從統計規律。（頻譜不確定，功率譜確定）；根據有用信號和干擾信號的功率譜設計濾波器——維納濾波（Wiener Filtering）或卡爾曼濾波（Kalman Filter）。

一、常規濾波

在圖像處理或者計算機應用中，在正式對圖像愛那個進行分析處理前一般需要一個預處理的過程。預處理是對圖像作一些諸如降維、降噪的操作，主要是為后續處理提供一個體積合適、只包含所需信息的圖像，通常會用到一些濾波處理手法。濾波，實際上就是信號處理，而圖像本身可以看作是一個二維信號，其中像素點灰度的高低代表信號的強弱。對應的高低頻的意義：

高頻：圖像中灰度變化強烈的點，一般是輪廓或者是噪聲。

低頻：圖像中平坦的，灰度變化不大的點，圖像中的大部各區域。

而根據圖像的高頻與低頻的特征，可以設計相應的高通和低通濾波器，高通濾波可以檢測圖像中尖銳、變化明顯的地方，而低通濾波可以讓圖像變得光滑，濾除圖像中的噪聲、OpenCv中提供的低通濾波有線性的均值濾波器、高斯濾波器，非線性的雙邊濾波器、中值濾波器；高通濾波有基于Canny，Sobel算子的各種濾波。其實很多時候低通濾波和高通濾波其實是相互矛盾的，很多時候在邊緣檢測前需要通過低通濾波降噪，這里就需要調節參數在保證高頻的邊緣不丟失的前提下盡可能多的去處圖像的噪點。

這里使用頻域的高通和低通濾波。

低通

理想的低通濾波器的模版為：

$equation?tex=H%28u%2Cv%29+%3D+%5Cbegin%7Bequation%7D+%5Cleft%5C%7B+%5Cbegin%7Barray%7D%7Blr%7D+1%2C+%5Cquad+D%28u%2C+v%29+%5Cle+D_0+%5C%5C++0%2C+%5Cquad+D%28u%2C+v%29+%5Cge+D_0+%5Cend%7Barray%7D+%5Cright.+%5Cend%7Bequation%7D$

其中，

$equation?tex=D_0$ 表示通帶半徑，

$equation?tex=D%28u%2C+v%29$ 是到頻譜中心的距離（歐式距離），計算公式如下：

$equation?tex=D%28u%2C+v%29+%3D+%5Csqrt+%7B%28u+-+M%2F+2%29%5E2+%2B+%28v-N%2F2%29%5E2%7D$ ，M和N表示頻譜圖像的大小，

$equation?tex=%28M%2F2%2C+N%2F2%29$ 即為頻譜中心。

def low_pass_filter(img, radius=100):r = radiusrows, cols = img.shapecenter = int(rows / 2), int(cols / 2)mask = np.zeros((rows, cols, 2), np.uint8)x, y = np.ogrid[:rows, :cols]mask_area = (x - center[0]) ** 2 + (y - center[1]) ** 2 <= r * rmask[mask_area] = 1return mask

Butterworth低通濾波器為：

$equation?tex=H%28u%2Cv%29+%3D+%5Cfrac%7B1%7D%7B1%2B%5B%5Cfrac%7BD%28u%2Cv%29%7D%7BD_0%7D%5D%5E%7B2n%7D%7D$

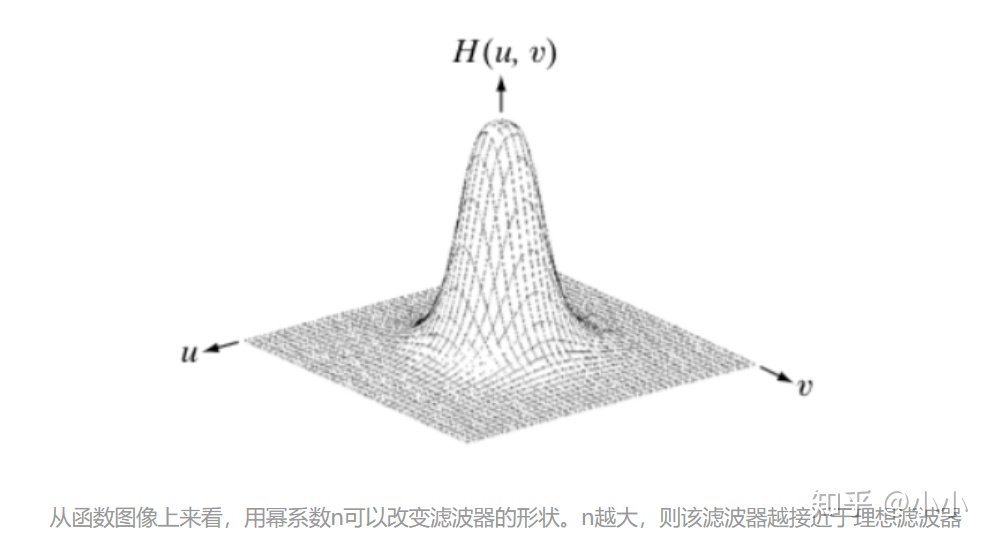
def Butterworth(src, d0, n, ftype):template = np.zeros(src.shape, dtype=np.float32)  # 構建濾波器r, c = src.shapefor i in np.arange(r):for j in np.arange(c):distance = np.sqrt((i - r/2)**2 + (j - c/2)**2)template[i, j] = 1/(1 + (distance/d0)**(2*n))  # Butterworth 濾波函數template[i, j] = np.e ** (-1 * (distance**2 / (2 * d0**2)))  # Gaussian濾波函數if ftype == 'high':template = 1 - templatereturn template

高斯低通濾波器：

$equation?tex=H%28u%2Cv%29+%3D+e%5E%7B%5Cfrac%7B-D%5E2%28u%2C+v%29%7D%7B2D_0%5E2%7D%7D$ ,1減去低通濾波器模板即可得到高通濾波器。

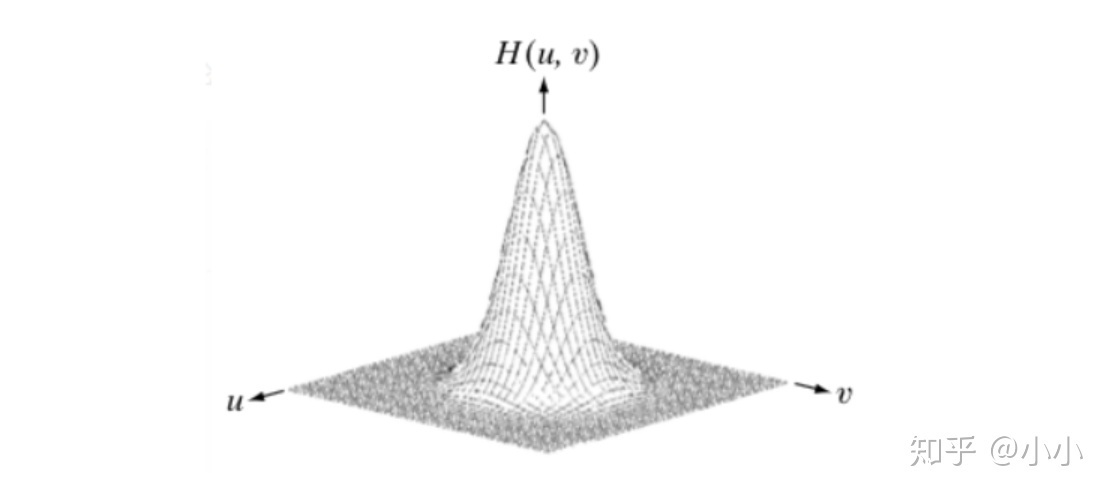
# 定義函數，高斯高/低通濾波模板
def Gaussian(src, d0, ftype):template = np.zeros(src.shape, dtype=np.float32)  # 構建濾波器r, c = src.shapefor i in np.arange(r):for j in np.arange(c):distance = np.sqrt((i - r / 2) ** 2 + (j - c / 2) ** 2)template[i, j] = np.e ** (-1 * (distance ** 2 / (2 * d0 ** 2)))  # Gaussian濾波函數if ftype == 'high':template = 1 - templatereturn template

帶通
帶阻

def bandreject_filters(img, r_out=300, r_in=35):rows, cols = img.shapecrow, ccol = int(rows / 2), int(cols / 2)radius_out = r_outradius_in = r_inmask = np.zeros((rows, cols, 2), np.uint8)center = [crow, ccol]x, y = np.ogrid[:rows, :cols]mask_area = np.logical_and(((x - center[0]) ** 2 + (y - center[1]) ** 2 >= r_in ** 2),((x - center[0]) ** 2 + (y - center[1]) ** 2 <= r_out ** 2))mask[mask_area] = 1mask = 1 - maskreturn mask

二、非局部均值濾波

圖像中的像素點之間不是孤立存在的，某一點的像素與別處的像素點一定存在著某種關聯，可以概括為灰度相關性和幾何結構相似性。

#coding:utf8
import cv2
import numpy as np
def psnr(A, B):return 10*np.log(255*255.0/(((A.astype(np.float)-B)**2).mean()))/np.log(10)def double2uint8(I, ratio=1.0):return np.clip(np.round(I*ratio), 0, 255).astype(np.uint8)def make_kernel(f):kernel = np.zeros((2*f+1, 2*f+1))for d in range(1, f+1):kernel[f-d:f+d+1, f-d:f+d+1] += (1.0/((2*d+1)**2))return kernel/kernel.sum()def NLmeansfilter(I, h_=10, templateWindowSize=5,  searchWindowSize=11):f = templateWindowSize/2t = searchWindowSize/2height, width = I.shape[:2]padLength = t+fI2 = np.pad(I, padLength, 'symmetric')kernel = make_kernel(f)h = (h_**2)I_ = I2[padLength-f:padLength+f+height, padLength-f:padLength+f+width]average = np.zeros(I.shape)sweight = np.zeros(I.shape)wmax =  np.zeros(I.shape)for i in range(-t, t+1):for j in range(-t, t+1):if i==0 and j==0:continueI2_ = I2[padLength+i-f:padLength+i+f+height, padLength+j-f:padLength+j+f+width]w = np.exp(-cv2.filter2D((I2_ - I_)**2, -1, kernel)/h)[f:f+height, f:f+width]sweight += wwmax = np.maximum(wmax, w)average += (w*I2_[f:f+height, f:f+width])return (average+wmax*I)/(sweight+wmax)if __name__ == '__main__':I = cv2.imread('lena.jpg', 0)sigma = 20.0I1 = double2uint8(I + np.random.randn(*I.shape) *sigma)print u'噪聲圖像PSNR',psnr(I, I1)R1  = cv2.medianBlur(I1, 5)print u'中值濾波PSNR',psnr(I, R1)R2 = cv2.fastNlMeansDenoising(I1, None, sigma, 5, 11)print u'opencv的NLM算法',psnr(I, R2)R3 = double2uint8(NLmeansfilter(I1.astype(np.float), sigma, 5, 11))print u'NLM PSNR',psnr(I, R3)

盡管opencv中已經有實現，對于彩色圖像，首先要先轉換到CIELAB顏色空間，然后對L和AB成分分別去噪。而且據說上面的實現會比opencv自帶的實現要好一些。

cv2.fastNlMeansDenoising() - 使用單個灰度圖像
cv2.fastNlMeansDenoisingColored() - 使用彩色圖像。
cv2.fastNlMeansDenoisingMulti() - 用于在短時間內捕獲的圖像序列（灰度圖像）
cv2.fastNlMeansDenoisingColoredMulti() - 與上面相同，但用于彩色圖像。fastNlMeansDenoisingColored( InputArray src, OutputArray dst,float h = 3, float hColor = 3,int templateWindowSize = 7, int searchWindowSize = 21)
參數：
? h : 決定過濾器強度。h 值高可以很好的去除噪聲,但也會把圖像的細節抹去。(取 10 的效果不錯)
? hForColorComponents : 與 h 相同,但使用與彩色圖像。(與 h 相同,10)
? templateWindowSize : 奇數。(推薦值為 7)
? searchWindowSize : 奇數。(推薦值為 21)

三、維納濾波

對于運動引起的模糊，最簡單的方法就是直接作逆濾波，但是逆濾波對于加性噪聲特別敏感，使得恢復的圖像幾乎不可用。最小均方差（維納）濾波用來去處含有噪聲的模糊圖像，其目標是找到未污染圖像的一個估計，使得他們之間的均方誤差最小，可以去除噪聲，同時清晰化模糊圖像。

主要參考：寫的不錯，有公式又證明！里面還有約束最小二乘方濾波！

https://blog.csdn.net/wsp_1138886114/article/details/95024180?blog.csdn.net

import matplotlib.pyplot as plt
import numpy as np
from numpy import fft
import math
import cv2# 仿真運動模糊
def motion_process(image_size, motion_angle):PSF = np.zeros(image_size)print(image_size)center_position = (image_size[0] - 1) / 2print(center_position)slope_tan = math.tan(motion_angle * math.pi / 180)slope_cot = 1 / slope_tanif slope_tan <= 1:for i in range(15):offset = round(i * slope_tan)  # ((center_position-i)*slope_tan)PSF[int(center_position + offset), int(center_position - offset)] = 1return PSF / PSF.sum()             # 對點擴散函數進行歸一化亮度else:for i in range(15):offset = round(i * slope_cot)PSF[int(center_position - offset), int(center_position + offset)] = 1return PSF / PSF.sum()# 對圖片進行運動模糊
def make_blurred(input, PSF, eps):input_fft = fft.fft2(input)             # 進行二維數組的傅里葉變換PSF_fft = fft.fft2(PSF) + epsblurred = fft.ifft2(input_fft * PSF_fft)blurred = np.abs(fft.fftshift(blurred))return blurreddef inverse(input, PSF, eps):                # 逆濾波input_fft = fft.fft2(input)PSF_fft = fft.fft2(PSF) + eps            # 噪聲功率，這是已知的，考慮epsilonresult = fft.ifft2(input_fft / PSF_fft)  # 計算F(u,v)的傅里葉反變換result = np.abs(fft.fftshift(result))return resultdef wiener(input, PSF, eps, K=0.01):        # 維納濾波，K=0.01input_fft = fft.fft2(input)PSF_fft = fft.fft2(PSF) + epsPSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + K)result = fft.ifft2(input_fft * PSF_fft_1)result = np.abs(fft.fftshift(result))return resultdef normal(array):array = np.where(array < 0,  0, array)array = np.where(array > 255, 255, array)array = array.astype(np.int16)return arraydef main(gray):channel = []img_h, img_w = gray.shape[:2]PSF = motion_process((img_h, img_w), 60)      # 進行運動模糊處理blurred = np.abs(make_blurred(gray, PSF, 1e-3))result_blurred = inverse(blurred, PSF, 1e-3)  # 逆濾波result_wiener = wiener(blurred, PSF, 1e-3)    # 維納濾波blurred_noisy = blurred + 0.1 * blurred.std() * np.random.standard_normal(blurred.shape)  # 添加噪聲,standard_normal產生隨機的函數inverse_mo2no = inverse(blurred_noisy, PSF, 0.1 + 1e-3)   # 對添加噪聲的圖像進行逆濾波wiener_mo2no = wiener(blurred_noisy, PSF, 0.1 + 1e-3)     # 對添加噪聲的圖像進行維納濾波channel.append((normal(blurred),normal(result_blurred),normal(result_wiener),normal(blurred_noisy),normal(inverse_mo2no),normal(wiener_mo2no)))return channelif __name__ == '__main__':image = cv2.imread('./gggg/001.png')b_gray, g_gray, r_gray = cv2.split(image.copy())Result = []for gray in [b_gray, g_gray, r_gray]:channel = main(gray)Result.append(channel)blurred = cv2.merge([Result[0][0][0], Result[1][0][0], Result[2][0][0]])result_blurred = cv2.merge([Result[0][0][1], Result[1][0][1], Result[2][0][1]])result_wiener = cv2.merge([Result[0][0][2], Result[1][0][2], Result[2][0][2]])blurred_noisy = cv2.merge([Result[0][0][3], Result[1][0][3], Result[2][0][3]])inverse_mo2no = cv2.merge([Result[0][0][4], Result[1][0][4], Result[2][0][4]])wiener_mo2no = cv2.merge([Result[0][0][5],  Result[1][0][5], Result[2][0][5]])#========= 可視化 ==========plt.figure(1)plt.xlabel("Original Image")plt.imshow(np.flip(image, axis=2))                         # 顯示原圖像plt.figure(2)plt.figure(figsize=(8, 6.5))imgNames = {"Motion blurred":blurred,"inverse deblurred":result_blurred,"wiener deblurred(k=0.01)":result_wiener,"motion & noisy blurred":blurred_noisy,"inverse_mo2no":inverse_mo2no,'wiener_mo2no':wiener_mo2no}for i,(key,imgName) in enumerate(imgNames.items()):plt.subplot(231+i)plt.xlabel(key)plt.imshow(np.flip(imgName, axis=2))plt.show()
OpenCV-Python 圖像去模糊（維納濾波，約束最小二乘方濾波）import matplotlib.pyplot as plt
import numpy as np
from numpy import fft
import math
import cv2# 仿真運動模糊
def motion_process(image_size, motion_angle):PSF = np.zeros(image_size)print(image_size)center_position = (image_size[0] - 1) / 2print(center_position)slope_tan = math.tan(motion_angle * math.pi / 180)slope_cot = 1 / slope_tanif slope_tan <= 1:for i in range(15):offset = round(i * slope_tan)  # ((center_position-i)*slope_tan)PSF[int(center_position + offset), int(center_position - offset)] = 1return PSF / PSF.sum()             # 對點擴散函數進行歸一化亮度else:for i in range(15):offset = round(i * slope_cot)PSF[int(center_position - offset), int(center_position + offset)] = 1return PSF / PSF.sum()# 對圖片進行運動模糊
def make_blurred(input, PSF, eps):input_fft = fft.fft2(input)             # 進行二維數組的傅里葉變換PSF_fft = fft.fft2(PSF) + epsblurred = fft.ifft2(input_fft * PSF_fft)blurred = np.abs(fft.fftshift(blurred))return blurreddef inverse(input, PSF, eps):                # 逆濾波input_fft = fft.fft2(input)PSF_fft = fft.fft2(PSF) + eps            # 噪聲功率，這是已知的，考慮epsilonresult = fft.ifft2(input_fft / PSF_fft)  # 計算F(u,v)的傅里葉反變換result = np.abs(fft.fftshift(result))return resultdef wiener(input, PSF, eps, K=0.01):        # 維納濾波，K=0.01input_fft = fft.fft2(input)PSF_fft = fft.fft2(PSF) + epsPSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + K)result = fft.ifft2(input_fft * PSF_fft_1)result = np.abs(fft.fftshift(result))return resultdef normal(array):array = np.where(array < 0,  0, array)array = np.where(array > 255, 255, array)array = array.astype(np.int16)return arraydef main(gray):channel = []img_h, img_w = gray.shape[:2]PSF = motion_process((img_h, img_w), 60)      # 進行運動模糊處理blurred = np.abs(make_blurred(gray, PSF, 1e-3))result_blurred = inverse(blurred, PSF, 1e-3)  # 逆濾波result_wiener = wiener(blurred, PSF, 1e-3)    # 維納濾波blurred_noisy = blurred + 0.1 * blurred.std() * np.random.standard_normal(blurred.shape)  # 添加噪聲,standard_normal產生隨機的函數inverse_mo2no = inverse(blurred_noisy, PSF, 0.1 + 1e-3)   # 對添加噪聲的圖像進行逆濾波wiener_mo2no = wiener(blurred_noisy, PSF, 0.1 + 1e-3)     # 對添加噪聲的圖像進行維納濾波channel.append((normal(blurred),normal(result_blurred),normal(result_wiener),normal(blurred_noisy),normal(inverse_mo2no),normal(wiener_mo2no)))return channelif __name__ == '__main__':image = cv2.imread('./gggg/001.png')b_gray, g_gray, r_gray = cv2.split(image.copy())Result = []for gray in [b_gray, g_gray, r_gray]:channel = main(gray)Result.append(channel)blurred = cv2.merge([Result[0][0][0], Result[1][0][0], Result[2][0][0]])result_blurred = cv2.merge([Result[0][0][1], Result[1][0][1], Result[2][0][1]])result_wiener = cv2.merge([Result[0][0][2], Result[1][0][2], Result[2][0][2]])blurred_noisy = cv2.merge([Result[0][0][3], Result[1][0][3], Result[2][0][3]])inverse_mo2no = cv2.merge([Result[0][0][4], Result[1][0][4], Result[2][0][4]])wiener_mo2no = cv2.merge([Result[0][0][5],  Result[1][0][5], Result[2][0][5]])#========= 可視化 ==========plt.figure(1)plt.xlabel("Original Image")plt.imshow(np.flip(image, axis=2))                         # 顯示原圖像plt.figure(2)plt.figure(figsize=(8, 6.5))imgNames = {"Motion blurred":blurred,"inverse deblurred":result_blurred,"wiener deblurred(k=0.01)":result_wiener,"motion & noisy blurred":blurred_noisy,"inverse_mo2no":inverse_mo2no,'wiener_mo2no':wiener_mo2no}for i,(key,imgName) in enumerate(imgNames.items()):plt.subplot(231+i)plt.xlabel(key)plt.imshow(np.flip(imgName, axis=2))plt.show()

四、卡爾曼濾波

Kalman filtering是一種利用線性系統狀態方程，通過系統輸入輸出觀測數據，對系統狀態進行最優估計的算法。Kalman濾波在測量方差已知的情況下能夠從一系列存在測量噪聲的數據中，估計動態系統的狀態。A Kalman filter is an optimal estimation algorithm. （最優化自回歸數據數據算法）

這都是百度百科的東西，搞得跟數學書上公式定理一樣，說的都不是人話！關鍵是字我都認識，但我沒懂什么意思。

1.1 是什么？

舉個例子：在海圖作業中，航海張通常以前一時刻的船位為基準，根據航向、船速和海流等一系列因素推算下一個船位，這個稱之為觀測船位；另外還會選擇適當的方法，通過儀器得到另一個推算船位，這個稱之為推算船位；觀測船位和推算船位一般都不重合，航海長需要通過分析和判斷選擇一個可靠的船位，作為船艦當前的位置。

由此得出卡爾曼濾波思想：以

$equation?tex=K-1$ 時刻的最有估計

$equation?tex=x_%7Bk-1%7D$ 為準，預測

$equation?tex=K$ 時刻的狀態變量

$equation?tex=%5Chat+x_%7Bk%2Fk-1%7D$ ，同時又對該狀態進行觀測，得到觀測變量

$equation?tex=z_k$ ，再在預測與預測之間進行分析，或者說是以觀測量對預測量進行修正，從而得到

$equation?tex=K$ 時刻的最有狀態估計

$equation?tex=x_k$ 。

卡爾曼濾波算法在控制領域有著極廣泛的應用，比如自動駕駛汽車，想象一下，一個雷達傳感器告訴你另一輛車距離15米，一個激光傳感器說車輛距離20米，那么如何協調這些傳感器測量。再比如，在發動機燃油噴射控制中，可以應用擴展的卡爾曼濾波理論研究瞬態工況下發動機循環進氣量的最有估計算法；在雷達中，人們最感興趣的是跟蹤目標，但目標的位置、速度、加速度的測量往往在任何時候都有噪聲，而卡爾曼濾波則是利用目標的動態信息，設法去除噪聲，得到一個關于目標位置的最好估計。

1.2 怎么回事？

再舉個例子：假設要研究一個房間的溫度，以一分鐘位時間單位，根據經驗判斷，這個房間的溫度是恒定的，但是對于我們的經驗不是完全相信，可能存在上下幾度的偏差，我們把該偏差看作是高斯白噪聲。另外，在房間里放一個溫度計，而溫度計也不準確，測量值會與實際值存在偏差，我們也把這偏差看作是高斯白噪聲。那么現在，我們要根據經驗溫度和溫度計的測量值以及他們各自的噪聲來估算出放房間的實際溫度。

那么接下來該如何解決呢？假如我們要估算

$equation?tex=k$ 時刻的實際溫度，首先要根據

$equation?tex=k-1$ 時刻的溫度值，來預測

$equation?tex=k$ 時刻的溫度（

$equation?tex=K$ 時刻的經驗溫度）。因為我們的經驗認為溫度是恒定的，所以會得到

$equation?tex=k$ 時刻的溫度和

$equation?tex=k-1$ 時刻是一樣的，假設是23度，同時該值（預測值）的高斯白噪聲為5度，（5是這樣得到的。如果k-1時刻估算出的最優溫度值的偏差是3，對自己預測的不確定度是4度，他們平方相加再開方，就是5），而溫度計得到的溫度值為25度，同時該值的偏差為4，此時，對于K時刻房間的溫度值有兩個：估計值23度和測量值25度，那么究竟相信誰？用均方根誤差判斷，

$equation?tex=H%5E2+%3D+%5Cfrac%7B5%5E2%7D%7B5%5E2+%2B+4%5E2%7D+%5CRightarrow+H+%3D+0.78$

所以估計K時刻最優溫度值為

$equation?tex=23%2B0.78%2A%2825-23%29%3D24.56$ 度，得到了K時刻的最優溫度，下一步就是對K+1時刻的溫度值進行最優估算，需要K時刻的最優溫度的偏差，

$equation?tex=%5Csqrt+%7B%281-H%29+%2A5%5E2%7D+%3D+2.35$

無控制離散型卡爾曼濾波基本方程

帶有控制的離散型卡爾曼濾波基本方程

詳情參照：[卡爾曼濾波器分類及其基本公式](卡爾曼濾波器分類及基本公式 - 百度文庫)

就這樣，卡爾曼濾波就能不斷吧均方誤差遞歸，從而估算出最優的溫度值，運行速度快，且只保留上一時刻的協方差。

總而言之，Kalman濾波用在當測量值與模型預測值均不準確的情況下，用來計算預測真值的一種濾波算法，在目標識別與追蹤任務中經常用到。

1.3 python代碼實現

def KalmanFilter(z, n_iter=20):# 這里是假設A=1，H=1的情況# intial parameterssz = (n_iter,)  # size of array# Q = 1e-5 # process varianceQ = 1e-6  # process variance# allocate space for arraysxhat = numpy.zeros(sz)  # a posteri estimate of xP = numpy.zeros(sz)  # a posteri error estimatexhatminus = numpy.zeros(sz)  # a priori estimate of xPminus = numpy.zeros(sz)  # a priori error estimateK = numpy.zeros(sz)  # gain or blending factorR = 0.1 ** 2  # estimate of measurement variance, change to see effect# intial guessesxhat[0] = 0.0P[0] = 1.0A = 1H = 1for k in range(1, n_iter):# time updatexhatminus[k] = A * xhat[k - 1]  # X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0Pminus[k] = A * P[k - 1] + Q  # P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1# measurement updateK[k] = Pminus[k] / (Pminus[k] + R)  # Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1xhat[k] = xhatminus[k] + K[k] * (z[k] - H * xhatminus[k])  # X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1P[k] = (1 - K[k] * H) * Pminus[k]  # P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1return xhat