我們知道,指數函數
![]()
,對于每一個確定值x,都有一個y值與它相對應。并且當x取不同值時,得到的函數值y也是不同的。也就是說指數函數的自變量與因變量是一一對應的。
對于任意的
![]()
,在R中都有唯一的數x滿足
![]()
。如果把y看做自變量,那么x就是y的函數。由對數的定義可知,這個函數可以表示為
![]()
。
通常習慣將自變量用x表示,所以這個函數可以寫成
![]()
。這種形式的函數稱為
其中函數的定義域為
![]()
,a叫做對數函數的
。
以10為底數的對數函數為常用對數函數,記作
![]()
;以無理數e為底的對數函數稱為
,記作
![]()
。
指數函數
![]()
和對數函數
![]()
描述同一對變量x,y之間的關系。在指數函數
![]()
中,函數定義域為實數集R,值域為
![]()
。在對數函數
![]()
中,定義域為
![]()
,值域為實數集R。像這樣的兩個函數稱作互為
。即對數函數
![]()
是指數函數
![]()
的反函數,指數函數
![]()
是對數函數
![]()
的反函數。
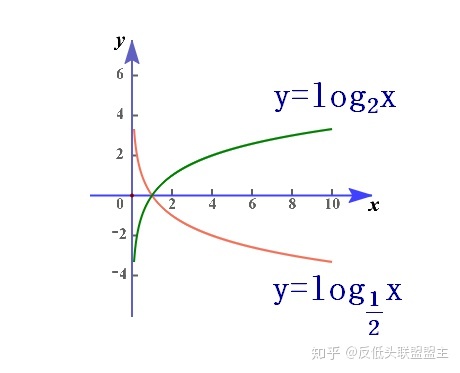
下面研究對數函數的性質,從特殊到一般,首先觀察a=2以及a=1/2時對數函數的圖像,如下所示:
可以看到,這兩根曲線只在y軸右側有值,且都經過點(1,0)。不同的是當a=2時,函數是上升的;當a=1/2時,函數是下降的。
對數函數
![]()
,當底數a>1或者0<a<1時函數的性質總結如下:
(1)兩者的定義域都為
![]()
,值域都為實數集。并且都經過點(1,0)
(2)當a>1時,函數為增函數;當0<a<1時,函數為減函數。
(3)當a>1時,若x>1,則y>0,若0<x<1,則y<0;當0<a<1時,若x>1,則y<0,若0<x<1,則y>0。
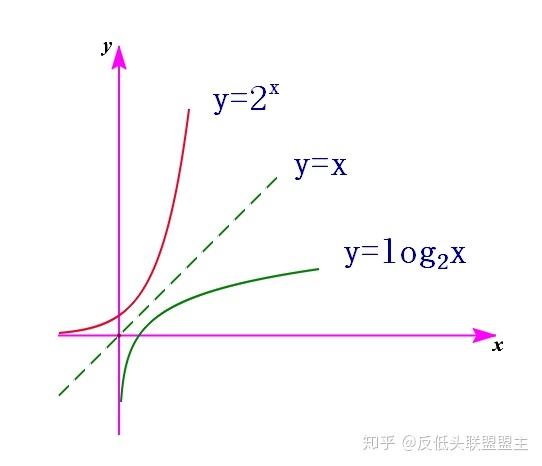
最后還應該看到,由于指數函數
![]()
和對數函數
![]()
互為反函數,其函數圖像關于直線y=x對稱。假設a=2,兩個函數圖像如下圖所示,可以看到這兩個函數的圖像關于y=x對稱。
由于函數
![]()
和函數
![]()
的圖像關于直線y=x對稱,所以只要記住了指數函數的特性,通過類比就能知道對數函數的特性。
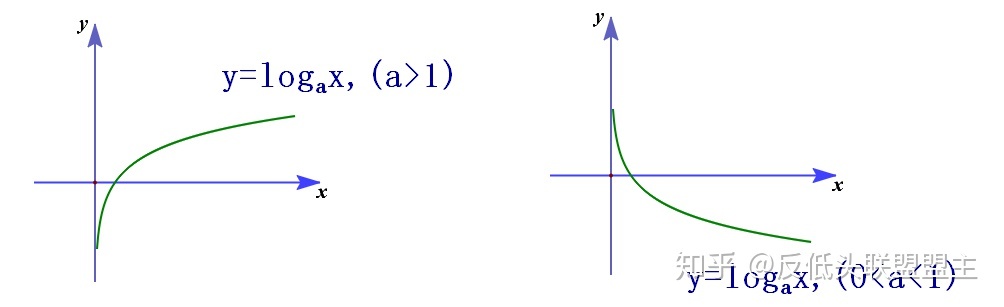













![mysql not in 轉化_[轉]mysql里not in語句怎么寫 | 學步園](http://pic.xiahunao.cn/mysql not in 轉化_[轉]mysql里not in語句怎么寫 | 學步園)

)
![如何判斷輸入的是字符還是數字_[Leetgo]判斷字符串是否為數字](http://pic.xiahunao.cn/如何判斷輸入的是字符還是數字_[Leetgo]判斷字符串是否為數字)


)