符號表的增刪查操作，隨著元素個數N的增多，其耗時也是線性增多的，時間復雜度都是O(n)，為了提高運算效率，我們學習樹這種數據結構。

目錄

一.樹的基本定義

二.樹的相關術語

三.二叉樹的基本定義

四.二叉樹的鏈表實現

1.二叉樹結點類：

結點類API設計

代碼實現

2.二叉樹API設計

3.二叉樹實現思想

五.二叉樹的基礎遍歷

前序遍歷

中序遍歷

后序遍歷

六.二叉樹的層序遍歷

七.二叉樹的最大深度問題

總結

---

一.樹的基本定義

樹是由n（n>=1）個有限結點組成一個具有層次關系的集合。把它叫做樹是因為它看起來像一顆倒掛的樹，也就是說它是根朝上，而葉朝下的。

?樹具有以下特點：
1.每個結點有零個或多個子結點；
2.沒有父結點的結點為根節點；
3.每一個非根結點只有一個父結點；
4.每個結點及其后代結點整體上可以看做是一棵樹，成為當前結點的父結點的一個子樹；

二.樹的相關術語

結點的度：
一個結點含有的子樹的個數稱為該結點的度
葉結點：
度為0的結點稱為葉結點，也可以叫做終端結點；
分支結點：
度不為0的結點稱為分支結點，也可以叫做非終端結點
結點的層次：
從根結點開始，根結點的層次為1，根的直接后繼層次為2，以此類推
結點的層序編號：
從樹中的結點，按照從上層到下層，同層從左到右的次序排成一個線性序列，把他們編成連續的自然數。
樹的度：
樹中所有結點的度的最大值
樹的高度(深度)：
樹中結點的最大層次
森林：
m（m>=0）個互不相交的樹的集合，將一個非空樹的根結點刪去，樹就變成了一個森林；給森林增加一個統一的根結點，森林就變成了一棵樹。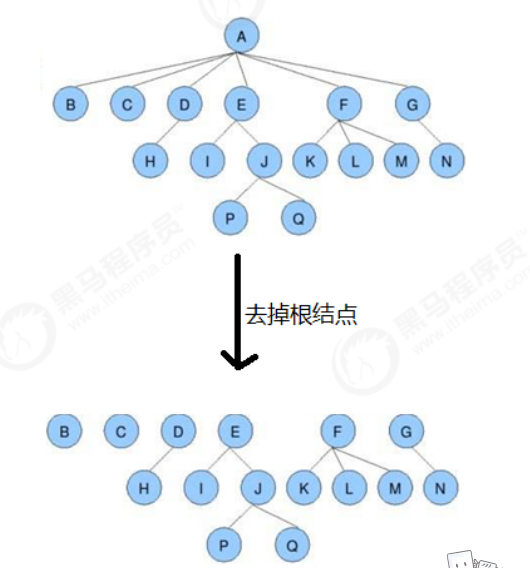

孩子結點：
一個結點的直接后繼結點稱為該結點的孩子結點
雙親結點（父節點）：
一個結點的直接前驅稱為該結點的雙親結點
兄弟結點：
同一雙親結點的孩子結點間互稱兄弟結點

三.二叉樹的基本定義

二叉樹就是度不超過2的樹（每個結點最多有兩個子結點）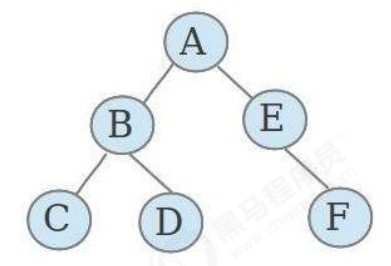

滿二叉樹：
一個二叉樹，如果每一個層的結點樹都達到最大值，則這個二叉樹就是滿二叉樹。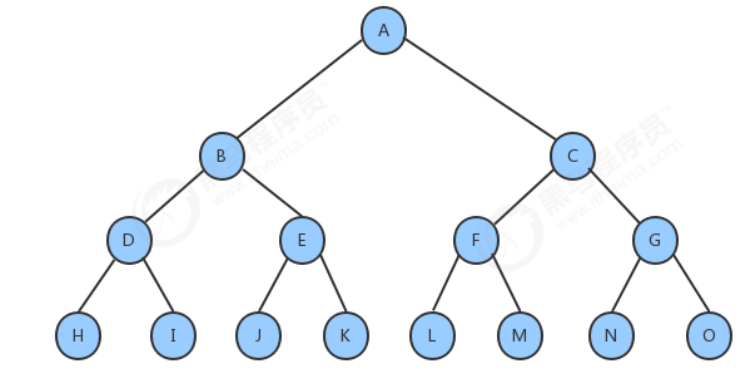

完全二叉樹：
葉節點只能出現在最下層和次下層，并且最下面一層的結點都集中在蓋層最左邊的若干位置的二叉樹。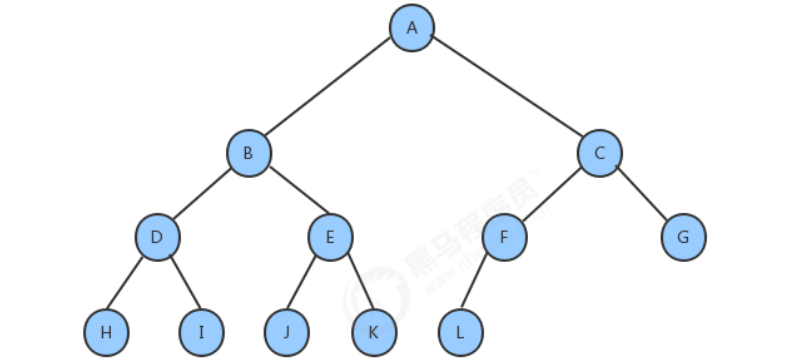

四.二叉樹的鏈表實現

1.二叉樹結點類：

按照面向對象的思想，我們設計一個結點類來描述結點這個事物。

結點類API設計:

代碼實現：

public class Node <Key,Vaule>{//存儲鍵public Key key;//存儲值public Value vaule;//記錄左子結點public Node left;//記錄右子結點public Node right;public Node(Key key, Value value, Node left, Node right){this.key=key;this.vaule=value;this.left=left;this.right=right;}
}

2.二叉樹API設計：

其他補充api：
private Node min(Node x)? ? ? ? 找出指定樹x中，最小鍵所在的結點
private Node max(Node x)? ? ? ? 找出指定樹x中，最大鍵所在的結點

3.二叉樹實現思想

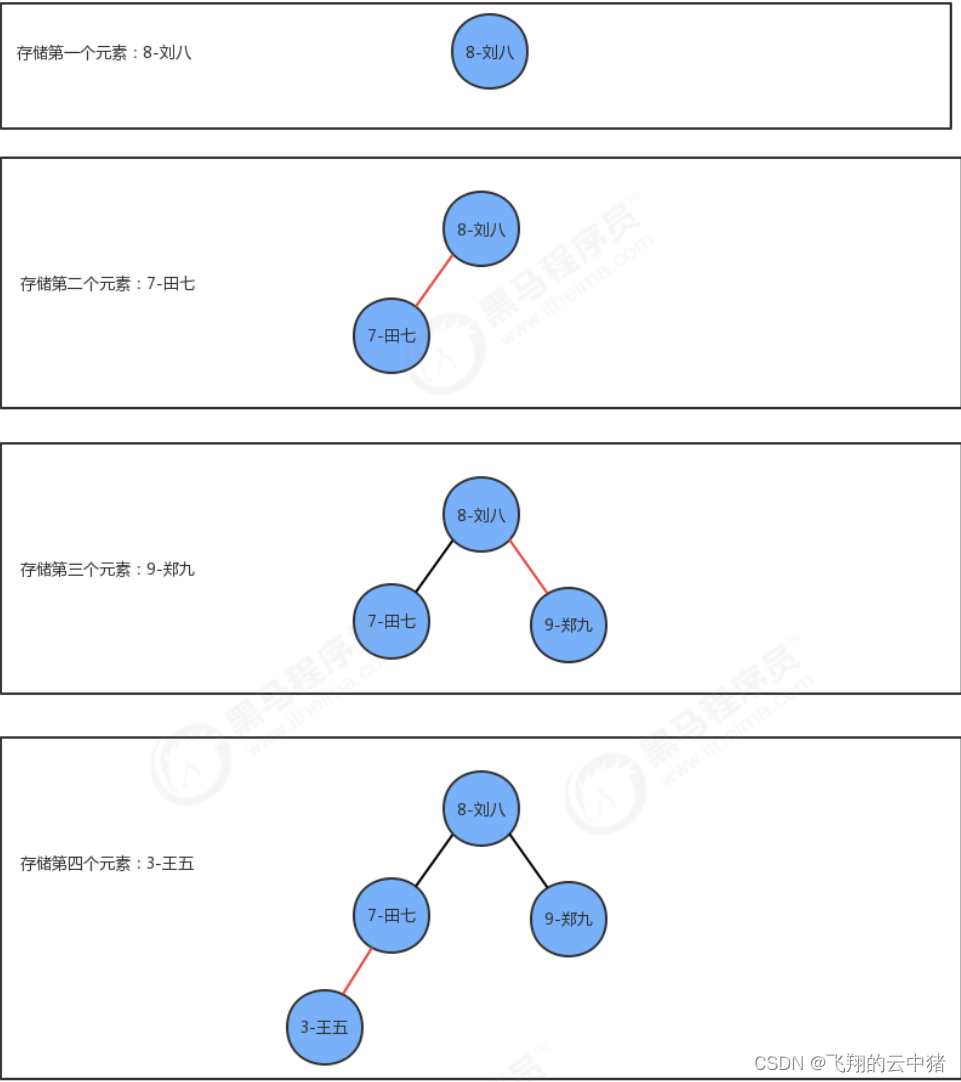
插入方法put實現思想：
1.如果當前樹中沒有任何一個結點，則直接把新結點當做根結點使用
2.如果當前樹不為空，則從根結點開始：
2.1 如果新結點的key小于當前結點的key，則繼續找當前結點的左子結點
2.2 如果新結點的key大于當前結點的key，則繼續找當前結點的右子結點
2.3 如果新結點等于當前結點的key，則樹中已經存在這樣的結點，替換該結點的value值即可。

查詢方法get實現思想：

從根節點開始：
1.如果要查詢的key小于當前結點的key，則繼續找當前結點的左子結點；
2.如果要查詢的key大于當前結點的key，則繼續找當前結點的右子結點；
3.如果要查詢的key等于當前結點的key，則樹中返回當前結點的value。

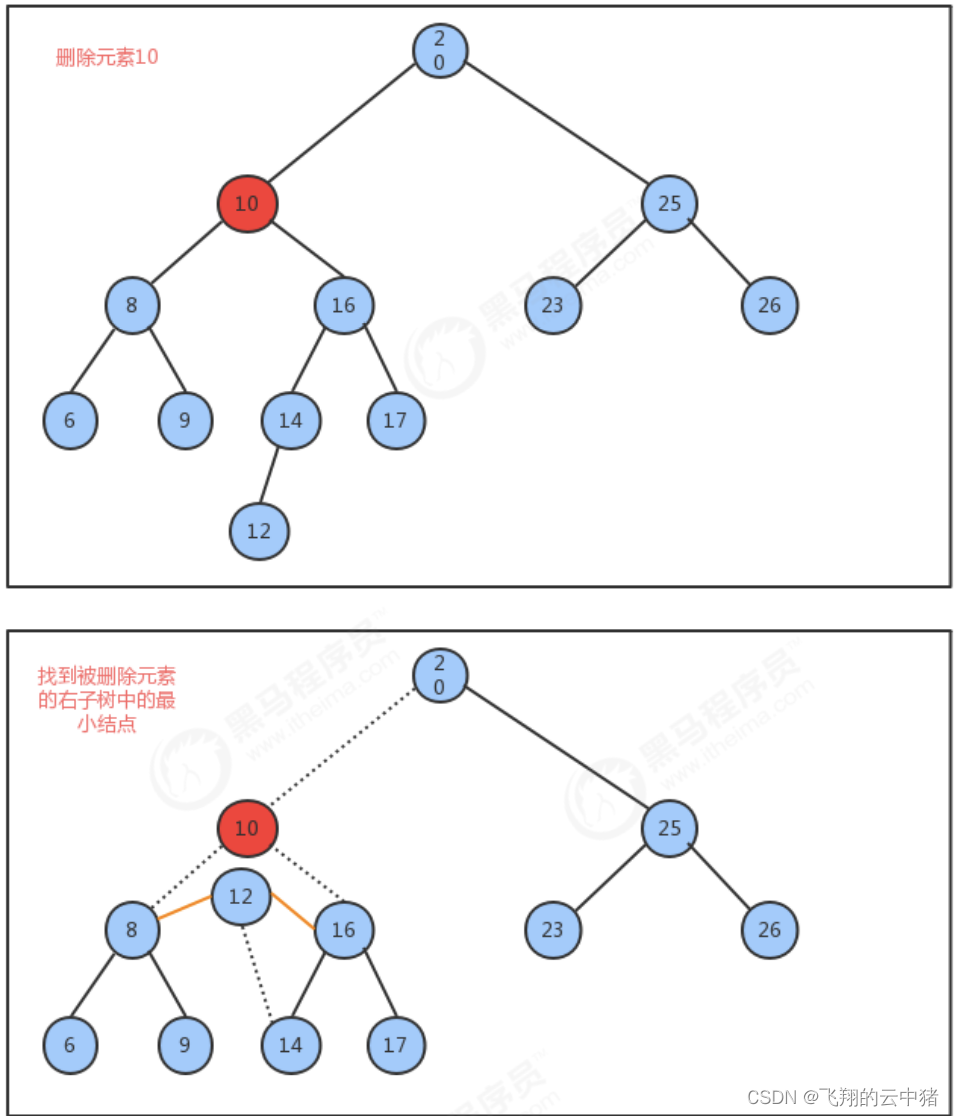
刪除方法delete實現思想：

1.找到被刪除結點
2.找到被刪除結點右子樹中的最小結點minNode
3.刪除右子樹中的最小結點
4.讓被刪除結點的左子樹稱為最小結點minNode的左子樹，讓被刪除結點的右子樹稱為最小結點minNode的右子樹
5.讓被刪除結點的父節點指向最小結點minNode

?

五.二叉樹的基礎遍歷

樹的結構和線性表結構不一樣，沒有辦法從頭開始依次向后遍歷，所以存在按照什么樣的搜索路徑進行遍歷的問題。

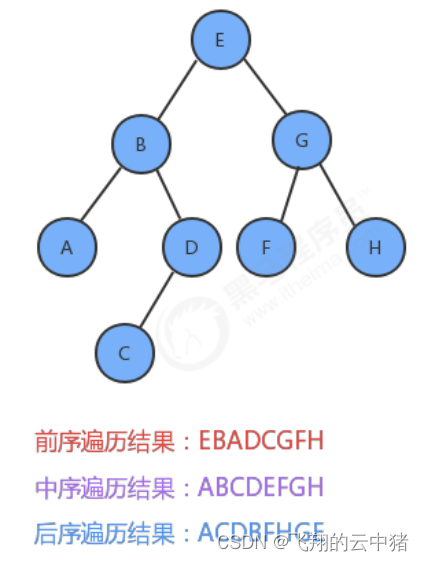
我們可以把二叉樹的遍歷分為以下三種（簡單說就是按什么時候訪問根節點進而分為前中后）：
1.前序遍歷：先訪問根節點，然后訪問左子樹，最后訪問右子樹。
2.中序遍歷：先訪問左子樹，中間訪問根節點，最后訪問右子樹。
3.后序遍歷：先訪問左子樹，再訪問右子數，最后訪問根節點。

可以看到其實就是三種操作變換順序罷了。

前序遍歷

實現步驟：
1.把當前結點的key放入到隊列中；
2.找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹；
3.找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹。

相關題目鏈接：

力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

中序遍歷

實現步驟：
1.找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹；
2.把當前結點的key放入到隊列中；
3.找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹。

相關題目鏈接：

力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

后序遍歷

實現步驟：
1.找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹；
2.把當前結點的key放入到隊列中；
3.找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹。

相關題目鏈接：
力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

六.二叉樹的層序遍歷

所謂層序遍歷，就是從根節點（第一層開始），依次向下，獲取每一層所有節點的值，
有二叉樹如下：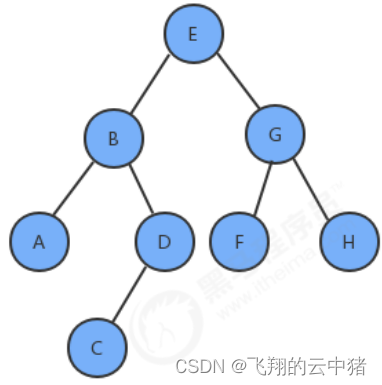

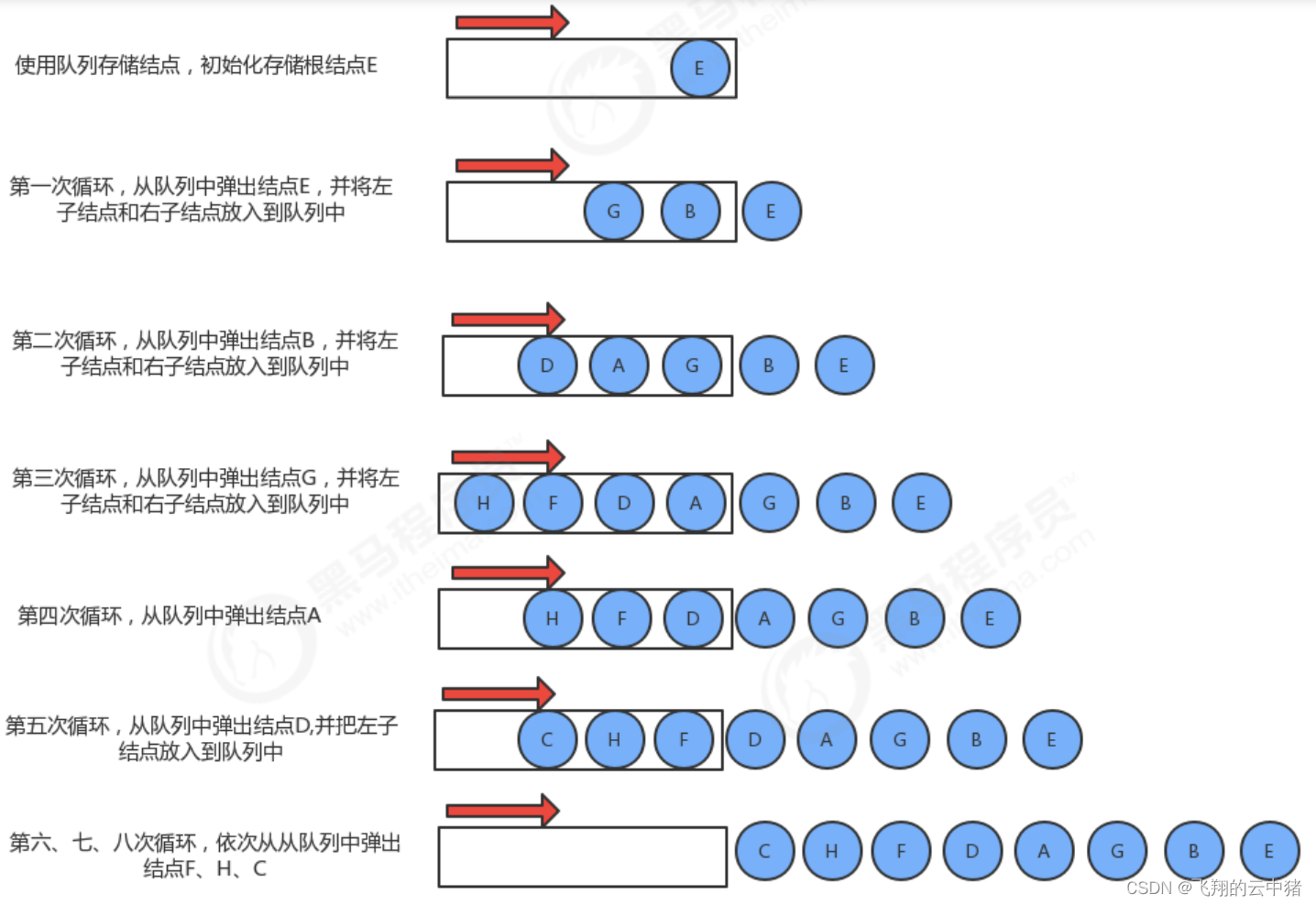
那么層序遍歷的結果是：EBGADFHC。

實現步驟：
1.創建隊列，存儲每一層的結點；
2.使用循環從隊列中彈出一個結點；
2.1獲取當前結點的key；
2.2如果當前結點的左子結點不為空，則把左子結點放入到隊列中；
2.3如果當前結點的右子結點不為空，則把右子結點放入到隊列中。

題目鏈接：
力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

七.二叉樹的最大深度問題

需求：給定一顆樹，計算樹的最大深度（樹的根節點到最遠葉子結點的最長路徑上的結點數）。

實現步驟：
1.如果根結點為空，則最大深度為0；
2.計算左子樹的最大深度；
3.計算右子樹的最大深度；
4.當前樹的最大深度=左子樹的最大深度和右子樹的最大深度中的較大者+1

題目鏈接：
力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

總結

可以看到關于樹的很多操作都要用到遞歸。