?
📙作者簡介:?清水加冰,目前大二在讀,正在學習C/C++、Python、操作系統、數據庫等。
📘相關專欄:C語言初階、C語言進階、C語言刷題訓練營、數據結構刷題訓練營、有感興趣的可以看一看。
歡迎點贊 👍 收藏 ?留言 📝 如有錯誤還望各路大佬指正!
?每一次努力都是一種收獲,每一次堅持都是一種成長?? ? ? ?
?

目錄
?
?前言
1. 特殊二叉樹
1.1 滿二叉樹
1.2 完全二叉樹
1.3 二叉樹的性質
2. 搜索二叉樹
3. 練習
📖?題目一
📖?題目二
📖?題目三?
總結
?
?
?前言
????????在計算機科學領域中,二叉樹作為一種重要的數據結構,被廣泛應用于各種算法和問題的解決方案中。然而,對于許多人來說,二叉樹仍然是一個神秘而復雜的概念。本篇博客將帶領你一同深入探索二叉樹的內在結構和特性,幫助你建立起對二叉樹的全面理解。
1. 特殊二叉樹
?????????前邊我們已經介紹了樹的結構,也了解了普通二叉樹,以及二叉樹的遍歷,今天我們將會繼續深入學習二叉樹。
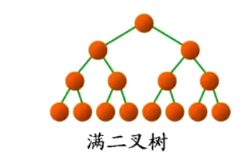
1.1 滿二叉樹
????????一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。也就是說,如果一個二叉樹的層數為K,且結點總數是 ,則它就是滿二叉樹。如下圖:
?1.2 完全二叉樹
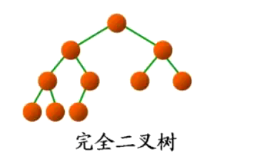
????????完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對于深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。(直白點說就是:假設有n層,前n-1層為滿二叉樹,最后一層的節點從左到右依次連接,不會出現一個節點連不滿的情況)
如下圖:
????????這樣的它就不屬于完全二叉樹:
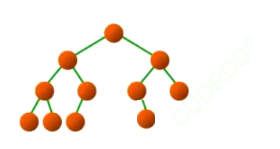
?因為從左到右,有節點沒有滿(從左到右節點必須連滿,不能出現有空)。
1.3 二叉樹的性質
- ?若規定根節點的層數為1,則一棵非空二叉樹的第i層上最多有 2???1?個結點.
- ?若規定根節點的層數為1,則深度為h的二叉樹的最大結點數是2?-1
- ?對任何一棵二叉樹, 如果度為0其葉結點個數為 , 度為2的分支結點個數為 ,則有?n?=n?+1(下標為二叉樹的度)
- ?若規定根節點的層數為1,具有n個結點的滿二叉樹的深度,h= log?(n+1)
????????對于具有n個結點的完全二叉樹,如果按照從上至下從左至右的數組順序對所有節點從0開始編號,則對于序號為i的結點有:
- 若i>0,i位置節點的雙親序號:(i-1)/2;i=0,i為根節點編號,無雙親節點
- ?若2i+1<n,左孩子序號:2i+1,2i+1>=n否則無左孩子
- ?若2i+2<n,右孩子序號:2i+2,2i+2>=n否則無右孩子
2. 搜索二叉樹
? ? ? ? 上述的二叉樹對于數據存儲沒什么特別規定與要求,屬于普通二叉樹大類,對于普通二叉樹來說,沒有增刪查改,普通二叉樹的增刪查改在現實應用中是沒有意義的(數據沒有特殊規定,無法確認新增節點的位置)。所以這里我們再來介紹一下其他的二叉樹——搜索二叉樹
?????????什么是搜索二叉樹?如下圖:
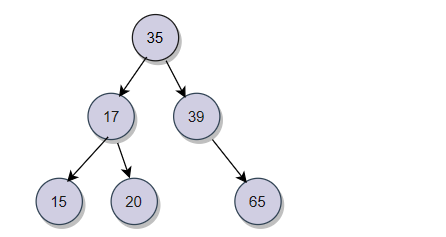
?????????任何一顆樹,左子樹都要比根小,右子樹都要比根大。搜索二叉樹的這個特性使得它的插入位置就可以確定。例如我們要插入一個數據38:

?????????從根開始,38比35大,就進入右子樹,38比39小,那就插入到39左子樹的位置。
例如我們再插入一個40:
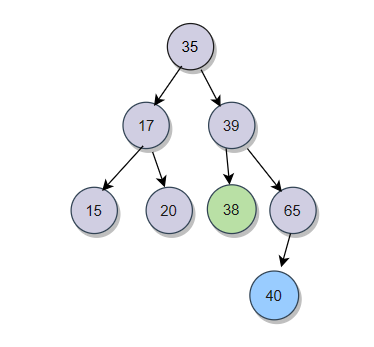
?????????從根開始,40比35大,就進入右子樹,40比39大,進入右子樹,40比65小,那就插入到65的左孩子節點位置。
????????如果我們要查找一個數,例如我們查找30,30比35小,進入左子樹,30比17大,進入右子樹,30比20大繼續進入到右子樹,但20沒有子節點,所以沒有30這個節點,到這里就停止尋找。通過這些例子我們可以發現,這樣的二叉樹很適合搜索。搜索二叉樹最多搜索高度次。
????????搜索的時間復雜度是O(N),細心的同學可能就會發現,搜素二叉樹最多搜素高度次,那二叉樹的高度不是有一個公式h= log?(n+1),時間復雜度為什么不是O(log N)?
? ? ? ? ?這里注意:這個二叉樹的高度公式針對的是滿二叉樹,而搜素二叉樹它可能出現退化的情況。如下圖:
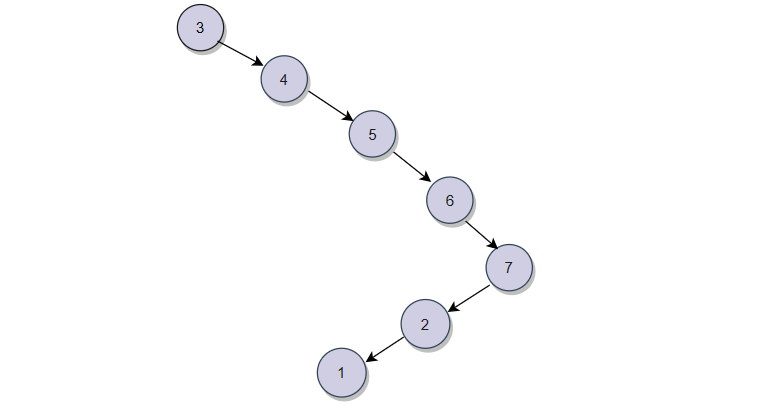
?最壞的情況:我們找1這個節點,它的時間復雜度就是O(N)。
那要如何避免這種情況的發生?使左右兩邊的節點數量均勻,又要保持這個特性。
?這里又可以引出一個新的概念——平衡樹
?平衡樹的特性就是:左右兩邊的節點數據比較均勻。
?平衡樹又可以分為:
- AVL樹
- 紅黑樹
?????????依照現在博客所講的水平,想要學會這兩種樹是不可能的,除此之外后續我們還會學習B樹,它是一種多叉搜索樹。數據庫的原理就與它有關。(此部分為了解)這部分的樹狀結構才是有用的東西,精髓就在這部分內容,這里我們后續會進行學習。
????????本期我們不會進行代碼的編寫介紹,我們要弄清楚二叉樹的性質,以及延申部分。接下來就是練習部分,幫助大家理解掌握二叉樹的性質。
?3. 練習
📖?題目一
1. 某二叉樹共有 399 個結點,其中有 199 個度為 2 的結點,則該二叉樹中的葉子結點數為 ?()
A、不存在這樣的二叉樹
B、200
C、198
D、199
?題目解析:
????????度為2的節點有199個,根據二叉樹的性質:n?=n?+1,度為0的節點個數等于度為2的節點個數+1。度為0的節點就為葉子節點。
?
正確答案:B
📖?題目二
2. 在具有 2n 個結點的完全二叉樹中,葉子結點個數為( )
A、n
B、n+1
C、n-1
D、n/2
?題目解析:
????????這道題目看似無解,突破口就在完全二叉樹。我們設度為0的節點個數為N0,度為1的節點個數為N1,度為2的節點個數為N2。根據性質可知:N0=N2+1,且N0+N1+N2=2n。
????????兩式聯合:N0+N1+N0-1=2n。
又因為這是一顆完全二叉樹,完全二叉樹度為1的節點只能有1個或沒有。但又要確保都為整數,所以度為1的節點就只要1個。即:N0+1+N0-1=2n
?
正確答案:A
📖?題目三?
3.一棵完全二叉樹的節點數位為531個,那么這棵樹的高度為( )
A、11
B、10
C、8
D、12
?題目解析:
????????題目要求這棵樹的高度,那就設樹的高度為h,最后一層缺了X個,根據定義我們可知:滿二叉樹是一種特殊的完全二叉樹。
? ? ? ? 由此可得出:2^h-1-X就是完全二叉樹的節點個數,即:2^h-1-X=531。到這里看似無解,但我們還可以根據性質進行推算,X的取值范圍是0? ~? 2^(h-1)-1,至少最后一層有1個節點,最多最后一次為滿(滿二叉樹),知道這些我們就可以帶選項進行推算了。代換:2^h-1-2^(h-1)+1。代入選項,看最終哪個選項的結果最接近500。
? ? ? ? 代入11,2的11次方:2048-1024=1024,如果高度是11那最少有1024個節點,A選項錯誤。這樣依次代入。
?
正確答案:B
總結
????????通過本篇博客我們對二叉樹的內在結構、特性,有了更全面的了解,希望通過本篇博客的閱讀,你已經掌握了深入理解二叉樹的關鍵知識。最后,感謝閱讀!
?












)





)
