注：此文只在個人總結 labuladong 動態規劃框架，僅限于學習交流，版權歸原作者所有；

也許有讀者看了前文 動態規劃詳解，學會了動態規劃的套路：找到了問題的「狀態」，明確了 dp 數組/函數的含義，定義了 base case；但是不知道如何確定「選擇」，也就是找不到狀態轉移的關系，依然寫不出動態規劃解法，怎么辦？

不要擔心，動態規劃的難點本來就在于尋找正確的狀態轉移方程，本文就借助經典的「最長遞增子序列問題」來講一講設計動態規劃的通用技巧：數學歸納思想。

最長遞增子序列（Longest Increasing Subsequence，簡寫 LIS）是非常經典的一個算法問題，比較容易想到的是動態規劃解法，時間復雜度 O(N^2)，我們借這個問題來由淺入深講解如何找狀態轉移方程，如何寫出動態規劃解法。比較難想到的是利用二分查找，時間復雜度是 O(NlogN)，我們通過一種簡單的紙牌游戲來輔助理解這種巧妙的解法。

力扣第 300 題「最長遞增子序列open in new window」就是這個問題：

輸入一個無序的整數數組，請你找到其中最長的嚴格遞增子序列的長度，函數簽名如下：

int lengthOfLIS(int[] nums);

比如說輸入 nums=[10,9,2,5,3,7,101,18]，其中最長的遞增子序列是 [2,3,7,101]，所以算法的輸出應該是 4。

注意「子序列」和「子串」這兩個名詞的區別，子串一定是連續的，而子序列不一定是連續的。下面先來設計動態規劃算法解決這個問題。

一、動態規劃解法

動態規劃的核心設計思想是數學歸納法。

相信大家對數學歸納法都不陌生，高中就學過，而且思路很簡單。比如我們想證明一個數學結論，那么我們先假設這個結論在 k < n 時成立，然后根據這個假設，想辦法推導證明出 k = n 的時候此結論也成立。如果能夠證明出來，那么就說明這個結論對于 k 等于任何數都成立。

類似的，我們設計動態規劃算法，不是需要一個 dp 數組嗎？我們可以假設 dp[0...i-1] 都已經被算出來了，然后問自己：怎么通過這些結果算出 dp[i]？

直接拿最長遞增子序列這個問題舉例你就明白了。不過，首先要定義清楚 dp 數組的含義，即 dp[i] 的值到底代表著什么？

我們的定義是這樣的：dp[i] 表示以 nums[i] 這個數結尾的最長遞增子序列的長度。

Info
為什么這樣定義呢？這是解決子序列問題的一個套路，后文 動態規劃之子序列問題解題模板 總結了幾種常見套路。你讀完本章所有的動態規劃問題，就會發現 dp 數組的定義方法也就那幾種。

根據這個定義，我們就可以推出 base case：dp[i] 初始值為 1，因為以 nums[i] 結尾的最長遞增子序列起碼要包含它自己。

舉兩個例子：

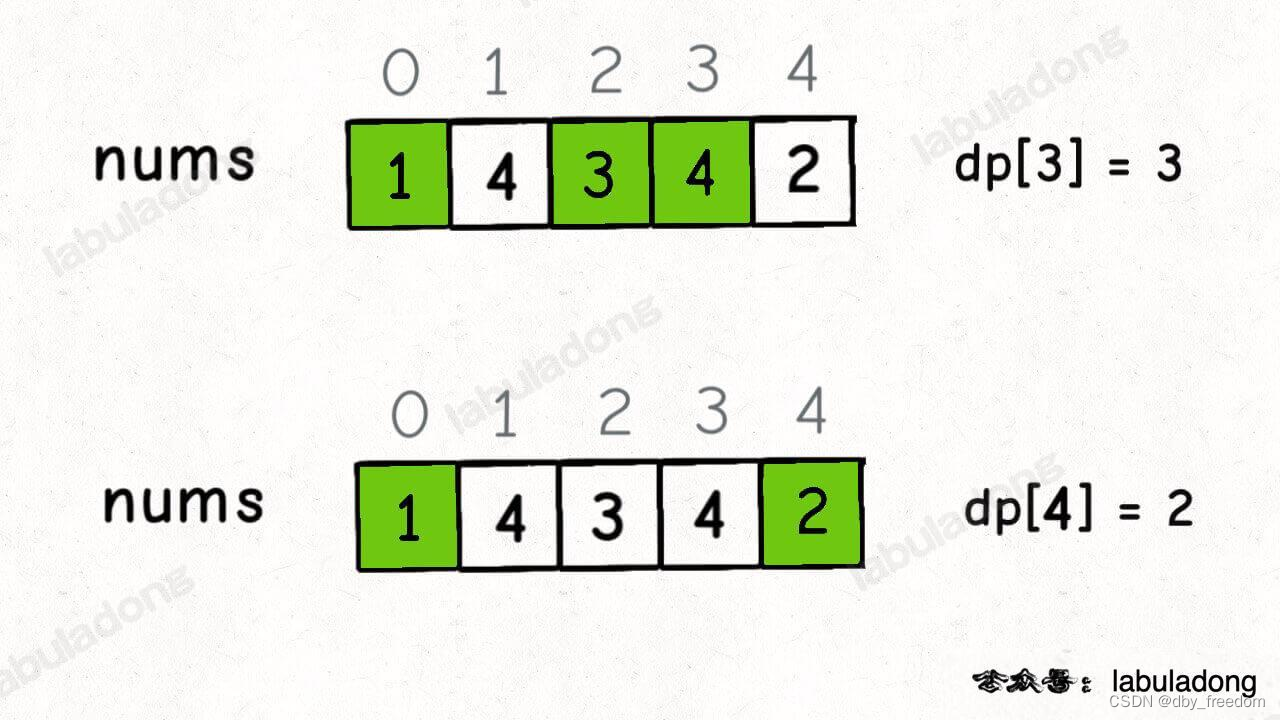
這個 GIF 展示了算法演進的過程：

根據這個定義，我們的最終結果（子序列的最大長度）應該是 dp 數組中的最大值。

int res = 0;
for (int i = 0; i < dp.length; i++) {res = Math.max(res, dp[i]);
}
return res;

讀者也許會問，剛才的算法演進過程中每個 dp[i] 的結果是我們肉眼看出來的，我們應該怎么設計算法邏輯來正確計算每個 dp[i] 呢？

這就是動態規劃的重頭戲，如何設計算法邏輯進行狀態轉移，才能正確運行呢？這里需要使用數學歸納的思想：

假設我們已經知道了 dp[0..4] 的所有結果，我們如何通過這些已知結果推出 dp[5] 呢？

根據剛才我們對 dp 數組的定義，現在想求 dp[5] 的值，也就是想求以 nums[5] 為結尾的最長遞增子序列。

nums[5] = 3，既然是遞增子序列，我們只要找到前面那些結尾比 3 小的子序列，然后把 3 接到這些子序列末尾，就可以形成一個新的遞增子序列，而且這個新的子序列長度加一。

nums[5] 前面有哪些元素小于 nums[5]？這個好算，用 for 循環比較一波就能把這些元素找出來。

以這些元素為結尾的最長遞增子序列的長度是多少？回顧一下我們對 dp 數組的定義，它記錄的正是以每個元素為末尾的最長遞增子序列的長度。

以我們舉的例子來說，nums[0] 和 nums[4] 都是小于 nums[5] 的，然后對比 dp[0] 和 dp[4] 的值，我們讓 nums[5] 和更長的遞增子序列結合，得出 dp[5] = 3：

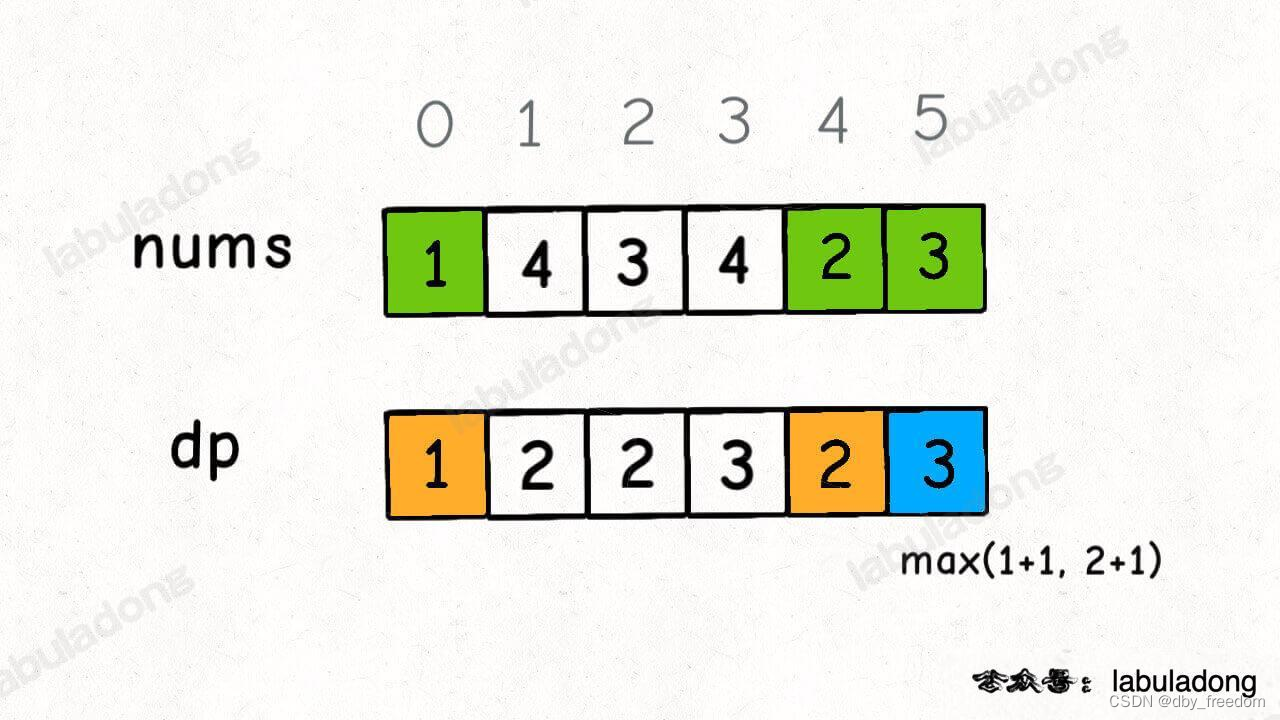
for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}
}

當 i = 5 時，這段代碼的邏輯就可以算出 dp[5]。其實到這里，這道算法題我們就基本做完了。

讀者也許會問，我們剛才只是算了 dp[5] 呀，dp[4], dp[3] 這些怎么算呢？類似數學歸納法，你已經可以算出 dp[5] 了，其他的就都可以算出來：

for (int i = 0; i < nums.length; i++) {for (int j = 0; j < i; j++) {// 尋找 nums[0..j-1] 中比 nums[i] 小的元素if (nums[i] > nums[j]) {// 把 nums[i] 接在后面，即可形成長度為 dp[j] + 1，// 且以 nums[i] 為結尾的遞增子序列dp[i] = Math.max(dp[i], dp[j] + 1);}}
}

結合我們剛才說的 base case，下面我們看一下完整代碼：

int lengthOfLIS(int[] nums) {// 定義：dp[i] 表示以 nums[i] 這個數結尾的最長遞增子序列的長度int[] dp = new int[nums.length];// base case：dp 數組全都初始化為 1Arrays.fill(dp, 1);for (int i = 0; i < nums.length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1);}}int res = 0;for (int i = 0; i < dp.length; i++) {res = Math.max(res, dp[i]);}return res;
}

---

至此，這道題就解決了，時間復雜度 O(N^2)。總結一下如何找到動態規劃的狀態轉移關系：

1、明確 dp 數組的定義。這一步對于任何動態規劃問題都很重要，如果不得當或者不夠清晰，會阻礙之后的步驟。

2、根據 dp 數組的定義，運用數學歸納法的思想，假設 dp[0...i-1] 都已知，想辦法求出 dp[i]，一旦這一步完成，整個題目基本就解決了。

但如果無法完成這一步，很可能就是 dp 數組的定義不夠恰當，需要重新定義 dp 數組的含義；或者可能是 dp 數組存儲的信息還不夠，不足以推出下一步的答案，需要把 dp 數組擴大成二維數組甚至三維數組。

目前的解法是標準的動態規劃，但對最長遞增子序列問題來說，這個解法不是最優的，可能無法通過所有測試用例了，下面講講更高效的解法。

注：核心問題是 2 個：

1. dp 數組的定義：最好能直接對應問題，如最長遞增子序列中 dp 數組表示以 nums[i] 結尾的最長的遞增最序列；
2. dp 數組的推理：即知道 dp[0...i-1] 都已知，如何求出 dp[i]；

其中 dp 數組如何定義很重要！

二、拓展到二維

我們看一個經常出現在生活中的有趣問題，力扣第 354 題「俄羅斯套娃信封問題open in new window」，先看下題目：

這道題目其實是最長遞增子序列的一個變種，因為每次合法的嵌套是大的套小的，相當于在二維平面中找一個最長遞增的子序列，其長度就是最多能嵌套的信封個數。

前面說的標準 LIS 算法只能在一維數組中尋找最長子序列，而我們的信封是由 (w, h) 這樣的二維數對形式表示的，如何把 LIS 算法運用過來呢？

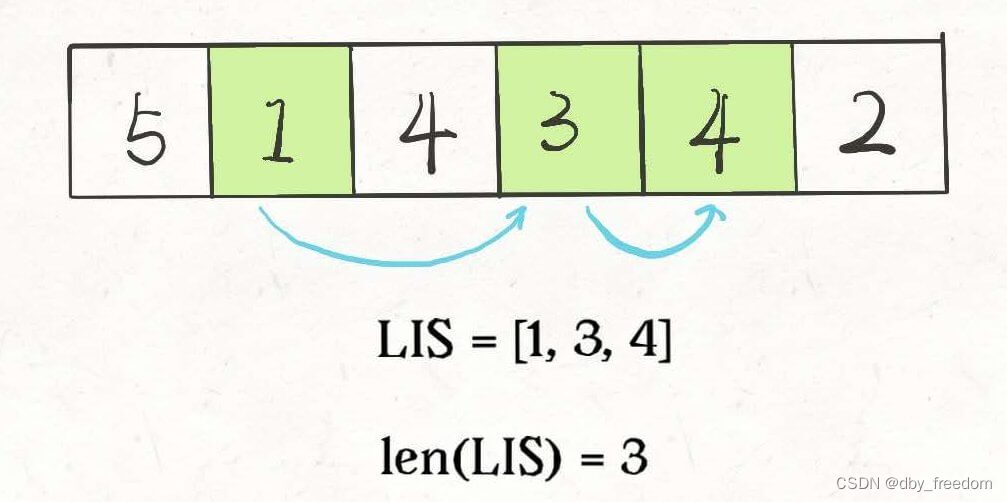
讀者也許會想，通過 w × h 計算面積，然后對面積進行標準的 LIS 算法。但是稍加思考就會發現這樣不行，比如 1 × 10 大于 3 × 3，但是顯然這樣的兩個信封是無法互相嵌套的。

這道題的解法比較巧妙：

先對寬度 w 進行升序排序，如果遇到 w 相同的情況，則按照高度 h 降序排序；之后把所有的 h 作為一個數組，在這個數組上計算 LIS 的長度就是答案。

畫個圖理解一下，先對這些數對進行排序：

然后在 h 上尋找最長遞增子序列，這個子序列就是最優的嵌套方案：

那么為什么這樣就可以找到可以互相嵌套的信封序列呢？稍微思考一下就明白了：

首先，對寬度 w 從小到大排序，確保了 w 這個維度可以互相嵌套，所以我們只需要專注高度 h 這個維度能夠互相嵌套即可。

其次，兩個 w 相同的信封不能相互包含，所以對于寬度 w 相同的信封，對高度 h 進行降序排序，保證二維 LIS 中不存在多個 w 相同的信封（因為題目說了長寬相同也無法嵌套）。

下面看解法代碼：

// envelopes = [[w, h], [w, h]...]
public int maxEnvelopes(int[][] envelopes) {int n = envelopes.length;// 按寬度升序排列，如果寬度一樣，則按高度降序排列Arrays.sort(envelopes, new Comparator<int[]>() {public int compare(int[] a, int[] b) {return a[0] == b[0] ? b[1] - a[1] : a[0] - b[0];}});// 對高度數組尋找 LISint[] height = new int[n];for (int i = 0; i < n; i++)height[i] = envelopes[i][1];return lengthOfLIS(height);
}int lengthOfLIS(int[] nums) {// 見前文
}

---

為了清晰，我將代碼分為了兩個函數， 你也可以合并，這樣可以節省下 height 數組的空間。

此處放上 Leetcode 官方答案，個人覺著解釋的更清晰一些：

根據題目的要求, 如果我們選擇了 $k$ 個信封, 它們的的寬度依次為 $w_0,w_1,?,w_{k?1}$, 高度依次為
$h_0,h_1,?,h_{k?1}$, 那么需要滿足: $$\{\begin{array}{l}{w}_0<w_1<?<w_{k?1}\\ h_0<h_1<?<h_{k?1}\end{array}$$
同時控制 $w$ 和 $h$ 兩個維度并不是那么容易, 因此我們考慮固定一個維度, 再在另一個維度上進行選 擇。例如, 我們固定 $w$
維度, 那么我們將數組 envelopes 中的所有信封按照 $w$ 升序排序。這樣一 來,
我們只要按照信封在數組中的出現順序依次進行選取, 就一定保證滿足: $$w_0\le w_1\le ?\le w_{k?1}$$ 了。然而小于等于 $\le$ 和小于 $<$ 還是有區別的，但我們不妨首先考慮一個簡化版本的問題:
如果我們保證所有信封的 w 值互不相同, 那么我們可以設計出一種得到答案的方法嗎? 在 $w$ 值互不相同的前提下，小于等于 $\le$
和小于 $<$ 是等價的，那么我們在排序后，就可以完全忽略 $w$ 維度, 只需要考慮 $h$ 維度了。此時, 我們需要解決的問題即為:
給定一個序列, 我們需要找到一個最長的子序列, 使得這個子序列中的元素嚴格單調遞增, 即上面 要求的:
$$h_0<h_1<?<h_{k?1}>$$ 那么這個問題就是經典的「最長嚴格遞增子序列」問題了, 讀者可以參考力扣平臺的 300 . 最長遞增 子序列 及其 官方題解。最長嚴格遞增子序列的詳細解決方法屬于解決本題的前置知識點, 不是本文分析的重點, 因此這里不再贅述,會在方法一和方法二中簡單提及。 當我們解決了簡化版本的問題之后, 我們來想一想使用上面的方法解決原問題, 會產生什么錯誤。當 $w$
值相同時，如果我們不規定 $h$ 值的排序順序，那么可能會有如下的情況： 排完序的結果為 $[(w,h)]=[(1,1),(1,2),(1,3),(1,4)]$, 由于這些信封的 $w$ 值都相同, 不存在一個 信封可以裝下另一個信封, 那么我們只能在其中選擇 1 個信封。然而如果我們完全忽略 $w$ 維度, 剩下的 $h$ 維度為 $[1,2,3,4]$,
這是一個嚴格遞增的序列, 那么我們就可以選擇所有的 4 個信封了, 這就產生了錯誤。 因此，我們必須要保證對于每一種 $w$ 值，我們最多只能選擇 1 個信封。 我們可以將 $h$ 值作為排序的第二關鍵字進行降序排序, 這樣一來, 對于每一種 $w$ 值, 其對應的信封 在排序后的數組中是按照 $h$ 值遞減的順序出現的, 那么這些 $h$ 值不可能組成長度超過 1 的嚴格遞增的序列，這就從根本上杜絕了錯誤的出現。 因此我們就可以得到解決本題需要的方法:

• 首先我們將所有的信封按照 $w$ 值第一關鍵字升序、 $h$ 值第二關鍵字降序進行排序;
• 隨后我們就可以忽略 $w$ 維度, 求出 $h$ 維度的最長嚴格遞增子序列, 其長度即為答案。 下面簡單提及兩種計算最長嚴格遞增子序列的方法, 更詳細的請參考上文提到的題目以及對應的官方 題解。

最后賦上個人題解：

    def maxEnvelopes(self, envelopes):""":type envelopes: List[List[int]]:rtype: int"""envelopes.sort(key = lambda x: (x[0], -x[1]))# heigth = [1] * len(envelopes)# for i in range(len(envelopes)):#     heigth[i] = envelopes[i][1]# return self.lcs(heigth)return self.lcsPro(envelopes)def lcs(self, heigth):if len(heigth) <= 1:return 1dp = [1] * len(heigth)for i in range(len(heigth)):for j in range(i):if heigth[i] > heigth[j]:dp[i] = max(dp[i], dp[j] + 1)return max(dp)def lcsPro(self, envelopes):if len(envelopes) <= 1:return 1dp = [1] * len(envelopes)for i in range(len(envelopes)):for j in range(i):if envelopes[i][1] > envelopes[j][1]:dp[i] = max(dp[i], dp[j] + 1)return max(dp) ```

三、參考文獻

[1] 動態規劃設計：最長遞增子序列
[2] Leetcode 官方題解