本系列博文為深度學習/計算機視覺論文筆記，轉載請注明出處

標題：Progressive Growing of GANs for Improved Quality, Stability, and Variation

鏈接：[1710.10196] Progressive Growing of GANs for Improved Quality, Stability, and Variation (arxiv.org)

摘要

我們描述了一種新的生成對抗網絡（GANs）訓練方法。關鍵思想是逐步地使生成器和判別器增長：從低分辨率開始，隨著訓練的進行，我們添加新的層（layer），這些層模擬了越來越精細的細節。這不僅加速了訓練過程，還極大地穩定了訓練過程，使我們能夠生成前所未有質量的圖像，例如 $1024^2$ 分辨率的CELEBA圖像。我們還提出了一種簡單的方法來增加生成圖像的變化，并在無監督的CIFAR10數據集中實現了創紀錄的 $8.80$ 的Inception分數。

此外，我們描述了一些對于防止生成器和判別器之間不健康的競爭很重要的實現細節。最后，我們提出了一種用于評估GAN結果的新指標，既涉及圖像質量又涉及變化。作為額外的貢獻，我們構建了一個更高質量的CELEBA數據集版本。

1 引言

生成方法用于從高維數據分布（例如圖像）中產生新樣本，正在廣泛應用于語音合成（van den Oord等，2016a）、圖像轉換（Zhu等，2017；Liu等，2017；Wang等，2017）和圖像修復（Iizuka等，2017）等領域。目前，最突出的方法包括自回歸模型（van den Oord等，2016b;c）、變分自編碼器（VAE）（Kingma和Welling，2014）和生成對抗網絡（GAN）（Goodfellow等，2014）。目前，它們都有顯著的優勢和劣勢。自回歸模型（如PixelCNN）可以生成清晰的圖像，但評估速度較慢，并且由于直接模擬像素上的條件分布，它們沒有潛在表示，這可能限制了它們的適用性。VAE易于訓練，但由于模型的限制，往往會產生模糊的結果，盡管近期的工作正在改進這一點（Kingma等，2016）。GAN可以生成清晰的圖像，盡管僅限于相對較小的分辨率，并且變化有些有限，盡管近期取得了進展，訓練仍然不穩定（Salimans等，2016；Gulrajani等，2017；Berthelot等，2017；Kodali等，2017）。混合方法結合了這三種方法的各種優勢，但在圖像質量方面仍落后于GAN（Makhzani和Frey，2017；Ulyanov等，2017；Dumoulin等，2016）。

通常情況下，GAN由兩個網絡組成：生成器和判別器（也稱為評論家）。生成器從潛在編碼生成樣本，例如圖像，這些圖像的分布理想情況下應與訓練分布不可區分。由于通常不可能設計一個函數來判斷是否為這種情況，因此訓練一個判別器網絡來進行評估。由于網絡可微分，我們還可以獲得梯度，以引導兩個網絡朝著正確的方向進行調整。通常，生成器是主要關注的對象，判別器是一個自適應的損失函數，在生成器訓練完成后就會被丟棄。

這種表述存在多個潛在問題。當我們衡量訓練分布和生成分布之間的距離時，如果這些分布沒有實質性的重疊，即很容易區分開（Arjovsky和Bottou，2017），梯度可能指向更多或更少的隨機方向。最初，Jensen-Shannon散度被用作距離度量（Goodfellow等，2014），近期這種表述已經得到改進（Hjelm等，2017），并且已經提出了許多更穩定的替代方法，包括最小二乘（Mao等，2016b）、帶邊際的絕對偏差（Zhao等，2017）和Wasserstein距離（Arjovsky等，2017；Gulrajani等，2017）。我們的貢獻在很大程度上與這個持續的討論無關，我們主要使用改進的Wasserstein損失，但也嘗試了最小二乘損失。

由于更高的分辨率使得容易區分生成的圖像與訓練圖像（Odena等，2017），因此嚴重放大了梯度問題，生成高分辨率圖像變得困難。由于內存限制，大分辨率還需要使用較小的小批量，進一步影響訓練的穩定性。我們的關鍵洞察是，我們可以逐步地使生成器和判別器增長，從容易的低分辨率圖像開始，隨著訓練的進行，添加新的層，引入更高分辨率的細節。這極大地加速了訓練，并提高了高分辨率圖像的穩定性，我們將在第2節中討論。

GAN的表述并不明確要求生成模型代表整個訓練數據分布。傳統觀點認為圖像質量和變化之間存在權衡，但這一觀點最近受到了挑戰（Odena等，2017）。當前正在關注保留的變化程度，已經提出了各種方法來衡量它，包括Inception分數（Salimans等，2016）、多尺度結構相似性（MS-SSIM）（Odena等，2017；Wang等，2003）、生日悖論（Arora和Zhang，2017）以及顯式測試發現的離散模式數量（Metz等，2016）。我們將在第3節中描述鼓勵變化的方法，并在第5節中提出用于評估質量和變化的新指標。

第4.1節討論了對網絡初始化的微小修改，以實現不同層之間更平衡的學習速度。此外，我們觀察到通常困擾GAN的模式崩潰往往發生得非常快，僅在幾十個小批量內。通常，它們在判別器超調時開始，導致梯度夸張，然后會出現不健康的競爭，兩個網絡中的信號幅度升高。我們提出了一種機制來阻止生成器參與這種升級，克服了這個問題（第4.2節）。

我們使用CELEBA、LSUN、CIFAR10數據集來評估我們的貢獻。我們改進了CIFAR10的最佳發布Inception分數。由于在基準生成方法中通常使用的數據集分辨率較低，我們還創建了一個更高質量的CELEBA數據集版本，允許在輸出分辨率高達1024×1024像素進行實驗。該數據集和我們的完整實現可在 https://github.com/tkarras/progressive_growing_of_gans 找到，訓練好的網絡可在 https://drive.google.com/open?id=0B4qLcYyJmiz0NHFULTdYc05lX0U 找到，同時附帶結果圖像，以及一個說明性視頻，展示了數據集、附加結果和潛在空間插值，地址為 https://youtu.be/G06dEcZ-QTg 。

2 逐步增長的生成對抗網絡

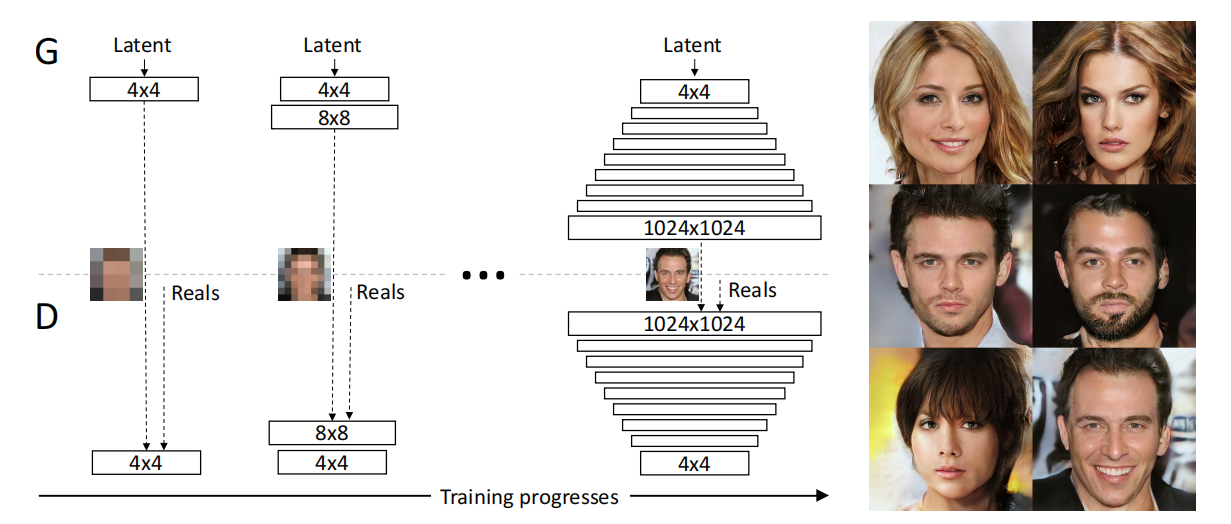
我們的主要貢獻是一種生成對抗網絡（GANs）的訓練方法，我們從低分辨率圖像開始，逐步增加分辨率，通過向網絡添加層，如圖1所示。這種漸進的方式使得訓練首先可以發現圖像分布的大尺度結構，然后將注意力轉移到越來越細的尺度細節，而不是必須同時學習所有尺度。

圖1：我們的訓練始于生成器（G）和判別器（D）的低分辨率狀態，為 4×4 像素。隨著訓練的進行，我們逐步向 G 和 D 添加層，從而增加生成圖像的空間分辨率。在整個過程中，所有現有的層都保持可訓練狀態。這里的 N × N 表示卷積層在 N × N 的空間分辨率上操作。這使得在高分辨率下能夠穩定地合成圖像，并且極大地加快了訓練速度。在右側，我們展示了使用漸進式增長生成的 1024 × 1024 分辨率的六個示例圖像。

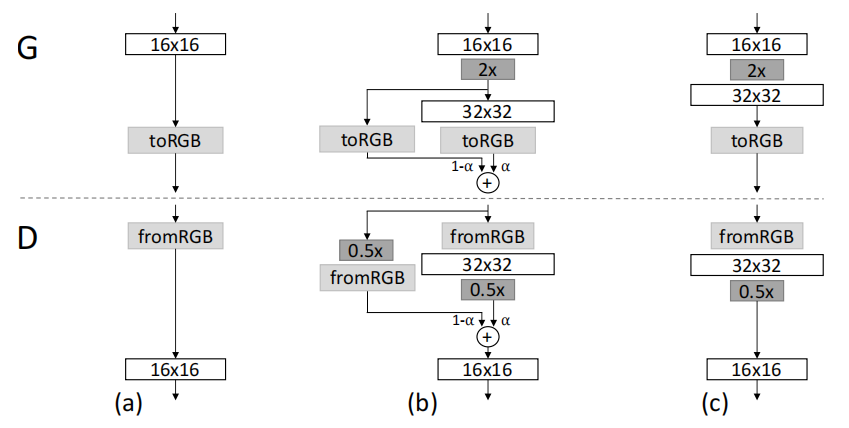
我們使用生成器和判別器網絡，它們是彼此的鏡像，始終同步增長。在整個訓練過程中，兩個網絡中的所有現有層都保持可訓練狀態。當向網絡添加新層時，我們會平滑地將它們淡入，如圖2所示。這避免了對已經訓練得很好的較小分辨率層造成突然的沖擊。附錄A詳細描述了生成器和判別器的結構，以及其他訓練參數。

圖2：當增加生成器（G）和判別器（D）的分辨率時，我們平滑地漸入新層。這個示例展示了從 16 × 16 圖像 (a) 到 32 × 32 圖像 ? 的過渡。在過渡期間 (b)，我們將在更高分辨率上操作的層視為一個殘差塊，其權重 α 從 0 線性增加到 1。這里的 2× 和 0.5× 分別表示使用最近鄰濾波和平均池化進行圖像分辨率的加倍和減半。toRGB 代表一個將特征向量投影到 RGB 顏色的層，而 fromRGB 則執行相反的操作；兩者都使用 1 × 1 卷積。在訓練判別器時，我們將實際圖像縮小以與網絡的當前分辨率匹配。在分辨率過渡期間，我們在實際圖像的兩個分辨率之間插值，類似于生成器輸出組合兩個分辨率的方式。

我們觀察到，漸進式訓練有幾個好處。早期，生成較小圖像的穩定性要更高，因為這里的類別信息較少，模式也較少（Odena等，2017）。通過逐漸增加分辨率，與從潛在向量到例如1024^2圖像的最終目標相比，我們一直在持續地提出一個更簡單的問題。這種方法在概念上與Chen和Koltun（2017）最近的工作有相似之處。在實踐中，它穩定了訓練，使我們能夠使用WGAN-GP損失（Gulrajani等，2017）甚至LSGAN損失（Mao等，2016b）可靠地合成百萬像素級別的圖像。另一個好處是減少的訓練時間。通過逐步增長的GANs，在較低分辨率下完成大部分迭代，通常可以在2-6倍的速度上獲得相當的結果質量，具體取決于最終的輸出分辨率。

漸進增長GANs的思想與Wang等（2017）的工作相關，他們使用多個判別器來操作不同的空間分辨率。這項工作受到Durugkar等（2016）的啟發，后者同時使用一個生成器和多個判別器，以及Ghosh等（2017），他們使用多個生成器和一個判別器。分層GANs（Denton等，2015；Huang等，2016；Zhang等，2017）為圖像金字塔的每個層級定義一個生成器和判別器。這些方法建立在與我們工作相同的觀察基礎上，即從潛在向量到高分辨率圖像的復雜映射在逐步學習中更容易實現，但關鍵的區別是我們只有一個單一的GAN，而不是一系列的GAN層級。與早期關于自適應增長網絡的工作相反，例如自適應增長神經氣體（Fritzke，1995）和增強拓撲的神經進化（Stanley和Miikkulainen，2002），這些方法會貪婪地增加網絡，我們只是延遲引入預配置的層。在這種意義上，我們的方法類似于自編碼器的逐層訓練（Bengio等，2007）。

3 使用小批量標準差增加變化

生成對抗網絡（GANs）往往只能捕捉到訓練數據中的一個子集的變化，Salimans等人（2016）提出了“小批量區分”作為解決方案。他們不僅從單個圖像計算特征統計信息，還從小批量中計算，從而鼓勵生成和訓練圖像的小批量顯示類似的統計信息。這是通過在判別器末尾添加一個小批量層來實現的，該層學習一個大張量，將輸入激活投影到一組統計數據中。對于小批量中的每個示例，都會生成一組單獨的統計數據，并將其連接到層的輸出，以便判別器可以在內部使用這些統計數據。我們在極大地簡化了這個方法的同時，也改善了變化。

我們的簡化解決方案既沒有可學習的參數，也沒有新的超參數。我們首先計算每個空間位置上的每個特征在小批量上的標準差。然后，我們將這些估計值在所有特征和空間位置上平均，得到一個單一的值。我們復制這個值，并將它連接到所有的空間位置和小批量上，從而產生一個額外的（恒定的）特征圖。這個層可以插入到判別器的任何位置，但我們發現將其插入到末尾是最好的（詳見附錄A.1）。我們嘗試了更豐富的統計數據集，但未能進一步改善變化。在平行的工作中，Lin等人（2017）就向判別器顯示多個圖像的益處提供了理論洞察。

解決變化問題的其他方法包括展開判別器（Metz等人，2016）以規范其更新，以及添加“排斥正則化器”（Zhao等人，2017）到生成器中，試圖鼓勵生成器在小批量中使特征向量正交。Ghosh等人（2017）的多個生成器也有類似的目標。我們承認，這些解決方案可能會進一步增加變化，甚至可能與我們的解決方案正交，但將詳細的比較留待以后。

4 生成器和判別器中的標準化

生成對抗網絡（GANs）容易因為兩個網絡之間的不健康競爭而導致信號幅度的升級。大多數情況下，如果不是全部情況，以前的解決方案都會使用批歸一化的變體（Ioffe＆Szegedy，2015；Salimans＆Kingma，2016；Ba等，2016）在生成器中使用，通常也會在判別器中使用。這些歸一化方法最初是引入的，以消除協變量偏移。然而，在GAN中，我們并沒有觀察到這是一個問題，因此我們認為GAN中的實際需求是約束信號幅度和競爭。我們使用了一個包含兩個成分的不同方法，其中都沒有可學習的參數。

4.1 均衡學習率

我們不同于當前謹慎權重初始化的趨勢，而是使用了一個簡單的 $N (0, 1)$ 初始化，然后在運行時明確地縮放權重。準確地說，我們設置 $w?_i = w_i/c$ ，其中 $w_i$ 是權重， $c$ 是來自He的初始化器（He等，2015）的每層歸一化常數。之所以在運行時而不是在初始化時執行這個操作的好處，有些微妙，與常用的自適應隨機梯度下降方法（例如RMSProp（Tieleman＆Hinton，2012）和Adam（Kingma＆Ba，2015））中的尺度不變性有關。這些方法通過其估計的標準差來歸一化梯度更新，從而使更新獨立于參數的尺度。因此，如果某些參數的動態范圍大于其他參數，它們將需要更長時間來調整。這是現代初始化器引起的情況，因此可能學習率同時過大和過小。我們的方法確保所有權重的動態范圍以及學習速度都相同。Van Laarhoven（2017）也獨立地使用了類似的推理。

4.2 生成器中的像素特征向量標準化

為了防止生成器和判別器中的幅度因競爭而失控的情況，我們在每個卷積層后將生成器中每個像素的特征向量歸一化為單位長度。我們使用一種“局部響應歸一化”的變體（Krizhevsky等人，2012），配置為

$b_{x,y} = \frac {a_{x,y}} {\sqrt {\frac{1}{N} \sum_{j=0}^{N-1}(a^j_{x,y}) ^ 2 + ε}}$

其中 $ε = 10^{-8}$ ， $N$ 是特征圖的數量， $a_{x,y}$ 和 $b_{x,y}$ 分別是像素 $(x, y)$ 中的原始和歸一化特征向量。令人驚訝的是，這種嚴格的約束似乎并沒有以任何方式損害生成器，實際上在大多數數據集上它并沒有太大地改變結果，但在需要時它能夠非常有效地防止信號幅度的升級。

5 用于評估GAN結果的多尺度統計相似性

為了將一個GAN的結果與另一個進行比較，需要調查大量圖像，這可能是繁瑣、困難且主觀的。因此，希望能依賴于自動化方法，從大型圖像集合中計算出一些指示性的度量。我們注意到，現有方法，如多尺度結構相似性（MS-SSIM）（Odena等人，2017），能夠可靠地發現大尺度的模式崩潰，但無法對顏色或紋理變化的較小效果做出反應，它們也不能直接從與訓練集的相似性來評估圖像質量。

我們基于這樣的直覺構建，即一個成功的生成器會產生出樣本，其局部圖像結構在所有尺度上都類似于訓練集。我們提出通過考慮從生成和目標圖像的拉普拉斯金字塔（Burt＆Adelson，1987）表示中提取的局部圖像塊的分布之間的多尺度統計相似性來研究這一點，從16×16像素的低通分辨率開始。按照標準做法，該金字塔逐漸倍增，直到達到完整的分辨率，每個連續的層級編碼到前一層級的上采樣版本的差異。

一個單一的拉普拉斯金字塔級別對應于特定的空間頻率帶。我們隨機采樣了16384張圖像，并從拉普拉斯金字塔的每個級別中提取了128個描述符，為每個級別給出了 $2^{21}$ （2.1M）個描述符。每個描述符是一個帶有3個顏色通道的 $7 \times 7$ 像素鄰域，用 $x ∈ R^{7×7×3} = R^{147}$ 表示。我們將訓練集和生成集中級別 $l$ 的圖像塊分別表示為 $\{x^l_i\}^{2^{21}}_{i=1}$ 和 $\{x^l_i\}^{2^{21}}_{i=1}$ ，我們首先根據每個顏色通道的均值和標準差對 $\{x^l_i\}$ 和 $\{y^l_i\}$ 進行歸一化，然后通過計算它們的切片Wasserstein距離 $SWD(\{x^l_i\}\{y^l_i\})$ 來估計統計相似性，這是對移動距離的有效可計算隨機估計，使用512個投影（Rabin等人，2011）。

直觀地，小的Wasserstein距離表明圖像塊的分布是相似的，這意味著訓練圖像和生成樣本在這個空間分辨率上看起來在外觀和變化方面都相似。特別是，從最低分辨率的 $16 \times 16$ 圖像中提取的塊集之間的距離指示了大尺度圖像結構的相似性，而最細級別的塊則編碼了有關像素級屬性（如邊緣的清晰度和噪聲）的信息。

6 實驗

本節討論了我們進行的一系列實驗，以評估我們結果的質量。有關網絡結構和訓練配置的詳細描述，請參見附錄A。我們還邀請讀者查閱附帶的視頻（ https://youtu.be/G06dEcZ-QTg ）以獲取更多的結果圖像和潛在空間插值。

在本節中，我們將區分網絡結構（例如，卷積層，調整大小）、訓練配置（各種規范化層，與小批量相關的操作）以及訓練損失（WGAN-GP，LSGAN）。

6.1 通過統計相似性評估各項貢獻的重要性

首先，我們將使用切片Wasserstein距離（SWD）和多尺度結構相似性（MS-SSIM）（Odena等人，2017）來評估我們各個貢獻的重要性，并對度量本身進行感知驗證。我們將在先前的狀態-of-the-art損失函數（WGAN-GP）和訓練配置（Gulrajani等人，2017）的基礎上進行構建，以無監督的方式使用CELEBA（Liu等人，2015）和LSUN BEDROOM（Yu等人，2015）數據集進行1282分辨率的測試。 CELEBA特別適合此類比較，因為訓練圖像包含難以忠實地再現的明顯偽影（混疊、壓縮、模糊等）。在此測試中，我們通過選擇相對低容量的網絡結構（附錄A.2）并在將總共顯示給判別器的真實圖像數量達到1000萬時終止訓練，放大了訓練配置之間的差異。因此，結果尚未完全收斂。

表1列出了幾種訓練配置中的SWD和MS-SSIM的數值，在基線（Gulrajani等人，2017）之上逐步啟用我們的各個貢獻。 MS-SSIM數字是從10000對生成的圖像中平均得出的，而SWD是如第5節所述計算得出的。這些配置生成的CELEBA圖像顯示在圖3中。由于篇幅限制，該圖只顯示了表中每行的一小部分示例，但在附錄H中提供了更廣泛的示例。直觀上，一個好的評估指標應該獎勵在顏色、紋理和視角方面表現出豐富變化的合理圖像。然而，MS-SSIM沒有捕捉到這一點：我們可以立即看出配置（h）生成的圖像明顯比配置（a）更好，但MS-SSIM基本保持不變，因為它僅測量輸出之間的變化，而不是與訓練集的相似性。另一方面，SWD確實表明了明顯的改進。

表1：在 128 × 128 分辨率下，不同訓練設置下生成圖像與訓練圖像之間的切片 Wasserstein 距離（SWD）（第 5 節）以及生成圖像之間的多尺度結構相似性（MS-SSIM）。對于 SWD，每一列代表拉普拉斯金字塔的一個層次，最后一列給出四個距離的平均值。

圖3：(a) – (g) 對應于表 1 中各行的 CELEBA 示例，這些示例故意是非收斂的。 (h) 我們的收斂結果。注意，一些圖像顯示出了鋸齒現象，一些圖像不夠清晰 - 這是數據集的一個缺陷，模型學會了忠實地復制這些特點。

第一個訓練配置（a）對應于Gulrajani等人（2017），其中生成器中有批歸一化，判別器中有層歸一化，小批量大小為64。 (b) 啟用了網絡的逐步增長，導致更銳利、更可信的輸出圖像。SWD正確地發現生成圖像的分布更類似于訓練集。我們的主要目標是實現高分辨率輸出，這需要減小小批量的大小，以使其適應可用的內存預算。我們在?中展示了隨著小批量大小從64減小到16所帶來的挑戰。生成的圖像是不自然的，這在兩個指標中都明顯可見。在(d)中，我們通過調整超參數以及去除批歸一化和層歸一化（附錄A.2）來穩定訓練過程。作為中間測試（e?），我們啟用了小批量判別（Salimans等人，2016），令人驚訝的是，它在任何指標上都沒有改善，包括衡量輸出變化的MS-SSIM。相反，我們的小批量標準差（e）提高了平均SWD分數和圖像質量。然后，在(f)和(g)中啟用了我們的其他貢獻，從而在SWD和主觀視覺質量方面都取得了改進。最后，在(h)中，我們使用非縮減的網絡和更長的訓練 - 我們認為生成的圖像質量至少與迄今為止發表的最佳結果相當。

6.2 收斂和訓練速度

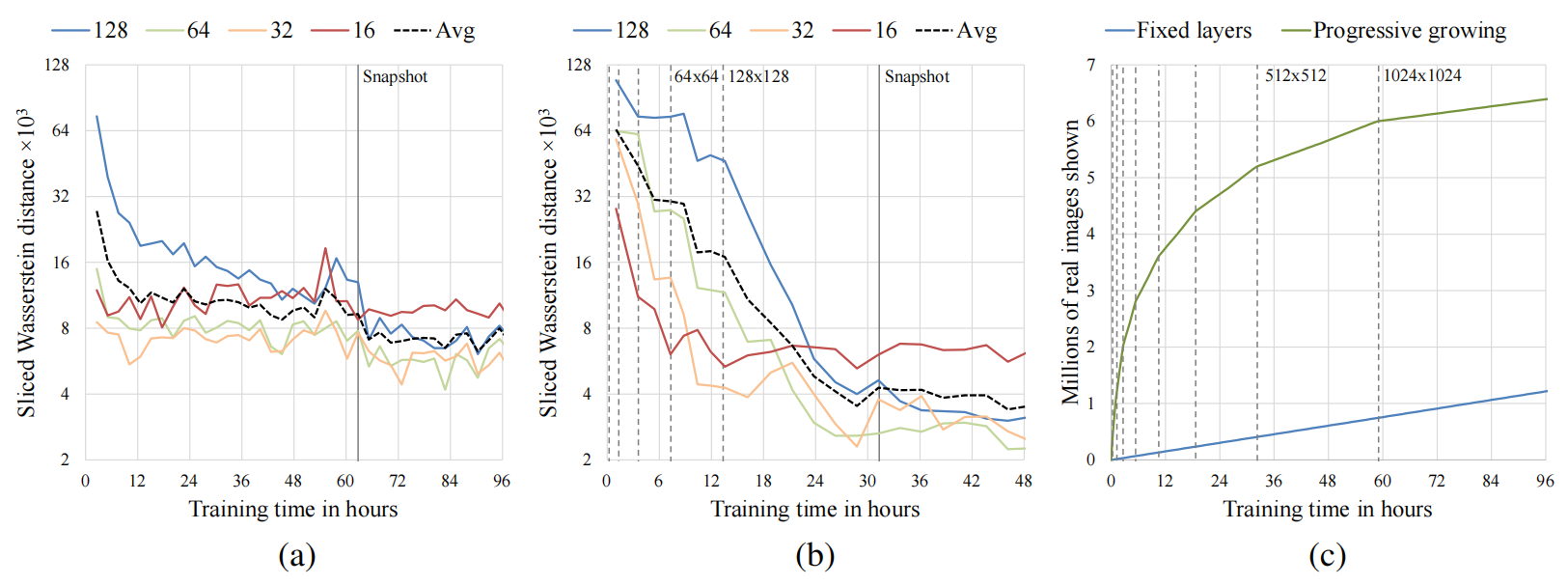
圖4說明了在SWD指標和原始圖像吞吐量方面，逐步增長對訓練的影響。前兩個圖對應于Gulrajani等人（2017）的訓練配置，沒有逐步增長和有逐步增長。我們觀察到，逐步增長變體提供了兩個主要優勢：它收斂到更好的極值，并且將總訓練時間減少了約兩倍。改進的收斂性是通過逐漸增加網絡容量所實施的一種隱式的課程學習來解釋的。沒有逐步增長，生成器和判別器的所有層都要同時為大尺度變化和小尺度細節找到簡潔的中間表示。然而，通過逐步增長，現有的低分辨率層在早期可能已經收斂，因此網絡只需要通過引入新層來逐漸減小尺度效應來精煉表示。的確，我們可以在圖4(b)中看到最大尺度統計相似性曲線（16）非常快速地達到其最佳值，并在其余訓練的過程中保持一致。較小尺度的曲線（32、64、128）隨著分辨率的增加逐一趨于平穩，但每個曲線的收斂都同樣一致。在圖4(a)中，非逐步增長訓練中，每個尺度的SWD指標大致同時收斂，這是可以預期的。

圖4：漸進增長對訓練速度和收斂的影響這些時間是在單 GPU 設置下，使用 NVIDIA Tesla P100 測量的。（a）使用 CELEBA 數據集在 128 × 128 分辨率下，針對 Gulrajani 等人（2017）方法，與墻上時鐘時間的統計相似性。每個圖表代表拉普拉斯金字塔的一個層次上的切片 Wasserstein 距離，垂直線指示我們在表 1 中停止訓練的點。（b）啟用漸進增長的相同圖表。虛線垂直線指示我們對 G 和 D 的分辨率加倍的點。（c）漸進增長對于 1024 × 1024 分辨率下原始訓練速度的影響。

逐步增長的加速度隨著輸出分辨率的增加而增加。圖4?顯示了在訓練過程中，以顯示給判別器的真實圖像數量為衡量標準，當訓練一直進行到1024 × 1024分辨率時的訓練時間的情況。我們可以看到，逐步增長變體因為網絡在開始時是淺層且快速評估，所以獲得了顯著的起步優勢。一旦達到完整分辨率，兩種方法之間的圖像吞吐量是相等的。圖表顯示，逐步變體在96小時內達到了大約640萬張圖像，而可以推測，非逐步變體將花費大約520小時才能達到相同的程度。在這種情況下，逐步增長提供了大約5.4倍的加速度。

6.3 使用CELEBA-HQ數據集生成高分辨率圖像

為了有意義地展示高輸出分辨率下的結果，我們需要一個足夠多樣且高質量的數據集。然而，先前在GAN文獻中使用的幾乎所有公開數據集都限制在相對較低的分辨率范圍內，從322到4802不等。為此，我們創建了一個高質量版本的CELEBA數據集，由30000張1024 × 1024分辨率的圖像組成。有關創建此數據集的更多細節，請參見附錄C。我們的貢獻使我們能夠以穩健且高效的方式處理高輸出分辨率。

圖5顯示了我們的網絡生成的選定1024 × 1024圖像。雖然在另一個數據集（Marchesi，2017）中已經展示過百萬像素GAN結果，但我們的結果更加多樣且具有更高的視覺質量。更多的結果圖像以及從訓練數據中找到的最近鄰示例，請參閱附錄F。隨附的視頻展示了潛在空間插值并可視化了逐步訓練。插值的工作方式是首先為每個幀隨機生成一個潛在編碼（從N（0,1）中單獨采樣的512個分量），然后使用高斯（σ = 45幀@60Hz)在時間上模糊潛在變量，最后將每個向量歸一化為超球面上的向量。

圖5：使用 CELEBA-HQ 數據集生成的 1024 × 1024 圖像。請參見附錄 F 獲取更大的結果集，以及附帶的視頻中的潛在空間插值。

我們使用8臺Tesla V100 GPU對網絡進行了4天的訓練，在此之后，我們不再觀察到連續訓練迭代的結果有質量上的差異。我們的實現根據當前輸出分辨率使用自適應小批量大小，以便最佳地利用可用內存預算。

為了證明我們的貢獻在很大程度上與損失函數的選擇無關，我們還使用了LSGAN損失而不是WGAN-GP損失對同一網絡進行了訓練。圖1顯示了使用LSGAN生成的六個10242圖像的示例。有關此設置的更多細節，請參見附錄B。

6.4 LSUN的結果

圖6在視覺上比較了我們的解決方案與先前在LSUN BEDROOM中的結果。圖7從2562的七個非常不同的LSUN類別中選擇了一些示例。來自所有30個LSUN類別的更大、非精選的結果集在附錄G中提供，視頻演示了插值。我們不知道在這些類別中有哪些先前的結果，盡管有些類別效果比其他類別更好，但我們認為總體質量較高。

圖6：在 LSUN BEDROOM 中的視覺質量比較；圖片來自引用的文章。

圖7：從不同的 LSUN 類別生成的 256 × 256 圖像選擇。

6.5 CIFAR10的Inception分數

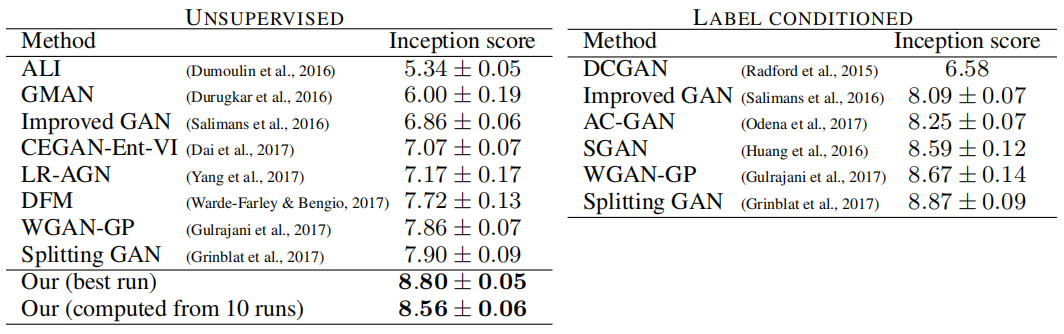
我們知道CIFAR10（32 × 32的RGB圖像的10個類別）的最佳Inception分數是7.90，而標簽條件設置的分數是8.87（Grinblat等人，2017）。兩個數字之間的巨大差異主要是由于在無監督設置中必然出現的“幽靈”（即類別之間的過渡）而引起的，而標簽條件設置可以消除許多這樣的過渡。

當啟用我們的所有貢獻時，我們在無監督設置下得到了8.80的分數。附錄D展示了一組生成圖像的代表性示例，以及早期方法的更全面的結果列表。網絡和訓練設置與CELEBA相同，當然，分辨率限制在32 × 32。唯一的定制是WGAN-GP的正則化項 $KaTeX parse error: Got function '\hat' with no arguments as subscript at position 14: E_{\hat{x}～P_\?h?a?t?{x}}[(||?\hat{x…$ 。Gulrajani等人（2017）使用了 $γ = 1.0$ ，這對應于1-Lipschitz，但我們注意到實際上最好是優先選擇快速過渡（ $γ = 750$ ），以最小化“幽靈”。我們沒有嘗試在其他數據集上使用這個技巧。

7 討論

雖然與GANs以前的工作相比，我們的結果質量通常較高，并且在高分辨率下的訓練是穩定的，但要達到真正的逼真程度還有很長的路要走。語義上的合理性和理解數據集特定的約束，比如某些物體是直的而不是彎曲的，仍有很大的改進空間。圖像的微觀結構也有提升的空間。盡管如此，我們認為令人信服的逼真感現在可能已經近在眼前，特別是在CELEBA-HQ數據集中。

8 致謝

我們要感謝Mikael Honkavaara、Tero Kuosmanen和Timi Hietanen提供的計算基礎設施。Dmitry Korobchenko和Richard Calderwood為CELEBA-HQ數據集相關工作所做的努力。Oskar Elek、Jacob Munkberg和Jon Hasselgren為有益的評論。

REFERENCES

Martin Arjovsky and L′eon Bottou. Towards principled methods for training generative adversarial networks. In ICLR, 2017.
Martin Arjovsky, Soumith Chintala, and L′eon Bottou. Wasserstein GAN. CoRR, abs/1701.07875, 2017.
Sanjeev Arora and Yi Zhang. Do GANs actually learn the distribution? an empirical study. CoRR, abs/1706.08224, 2017.
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton. Layer normalization. CoRR, abs/1607.06450, 2016.
Yoshua Bengio, Pascal Lamblin, Dan Popovici, and Hugo Larochelle. Greedy layer-wise training of deep networks. In NIPS, pp. 153–160. 2007.
David Berthelot, Tom Schumm, and Luke Metz. BEGAN: Boundary equilibrium generative adversarial networks. CoRR, abs/1703.10717, 2017.
Peter J. Burt and Edward H. Adelson. Readings in computer vision: Issues, problems, principles, and paradigms. Chapter: The Laplacian Pyramid As a Compact Image Code, pp. 671–679. 1987.
Qifeng Chen and Vladlen Koltun. Photographic image synthesis with cascaded refinement networks. CoRR, abs/1707.09405, 2017.
Zihang Dai, Amjad Almahairi, Philip Bachman, Eduard H. Hovy, and Aaron C. Courville. Calibrating energy-based generative adversarial networks. In ICLR, 2017.
Emily L. Denton, Soumith Chintala, Arthur Szlam, and Robert Fergus. Deep generative image models using a Laplacian pyramid of adversarial networks. CoRR, abs/1506.05751, 2015.
Vincent Dumoulin, Ishmael Belghazi, Ben Poole, Alex Lamb, Martin Arjovsky, Olivier Mastropietro, and Aaron Courville. Adversarially learned inference. CoRR, abs/1606.00704, 2016.
Ishan P. Durugkar, Ian Gemp, and Sridhar Mahadevan. Generative multi-adversarial networks. CoRR, abs/1611.01673, 2016.
Bernd Fritzke. A growing neural gas network learns topologies. In Advances in Neural Information Processing Systems 7, pp. 625–632. 1995.
Arnab Ghosh, Viveka Kulharia, Vinay P. Namboodiri, Philip H. S. Torr, and Puneet Kumar Dokania. Multi-agent diverse generative adversarial networks. CoRR, abs/1704.02906, 2017.
Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative Adversarial Networks. In NIPS, 2014.
Guillermo L. Grinblat, Lucas C. Uzal, and Pablo M. Granitto. Class-splitting generative adversarial networks. CoRR, abs/1709.07359, 2017.
Ishaan Gulrajani, Faruk Ahmed, Mart′?n Arjovsky, Vincent Dumoulin, and Aaron C. Courville. Improved training of Wasserstein GANs. CoRR, abs/1704.00028, 2017.
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. CoRR, abs/1502.01852, 2015.
Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. GANs trained by a two time-scale update rule converge to a local Nash equilibrium. In NIPS, pp. 6626–6637. 2017.
R Devon Hjelm, Athul Paul Jacob, Tong Che, Kyunghyun Cho, and Yoshua Bengio. Boundary-Seeking Generative Adversarial Networks. CoRR, abs/1702.08431, 2017.
Xun Huang, Yixuan Li, Omid Poursaeed, John E. Hopcroft, and Serge J. Belongie. Stacked generative adversarial networks. CoRR, abs/1612.04357, 2016.
Satoshi Iizuka, Edgar Simo-Serra, and Hiroshi Ishikawa. Globally and locally consistent image completion. ACM Trans. Graph., 36(4):107:1–107:14, 2017.
Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. CoRR, abs/1502.03167, 2015.
Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In ICLR, 2015.
Diederik P. Kingma and Max Welling. Auto-encoding variational Bayes. In ICLR, 2014.
Diederik P Kingma, Tim Salimans, Rafal Jozefowicz, Xi Chen, Ilya Sutskever, and Max Welling. Improved variational inference with inverse autoregressive flow. In NIPS, volume 29, pp. 4743–4751. 2016.
Naveen Kodali, Jacob D. Abernethy, James Hays, and Zsolt Kira. How to train your DRAGAN. CoRR, abs/1705.07215, 2017.
Dmitry Korobchenko and Marco Foco. Single image super-resolution using deep learning, 2017. URL: https://gwmt.nvidia.com/super-res/about. Machines Can See summit.
Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. ImageNet classification with deep convolutional neural networks. In NIPS, pp. 1097–1105. 2012.
Christian Ledig, Lucas Theis, Ferenc Huszar, Jose Caballero, Andrew P. Aitken, Alykhan Tejani, Johannes Totz, Zehan Wang, and Wenzhe Shi. Photo-realistic single image super-resolution using a generative adversarial network. CoRR, abs/1609.04802, 2016.
Zinan Lin, Ashish Khetan, Giulia Fanti, and Sewoong Oh. PacGAN: The power of two samples in generative adversarial networks. CoRR, abs/1712.04086, 2017.
Ming-Yu Liu, Thomas Breuel, and Jan Kautz. Unsupervised image-to-image translation networks. CoRR, abs/1703.00848, 2017.
Ziwei Liu, Ping Luo, Xiaogang Wang, and Xiaoou Tang. Deep learning face attributes in the wild. In ICCV, 2015.
Alireza Makhzani and Brendan J. Frey. PixelGAN autoencoders. CoRR, abs/1706.00531, 2017.
Xiao-Jiao Mao, Chunhua Shen, and Yu-Bin Yang. Image restoration using convolutional autoencoders with symmetric skip connections. CoRR, abs/1606.08921, 2016a.
Xudong Mao, Qing Li, Haoran Xie, Raymond Y. K. Lau, and Zhen Wang. Least squares generative adversarial networks. CoRR, abs/1611.04076, 2016b.
Marco Marchesi. Megapixel size image creation using generative adversarial networks. CoRR, abs/1706.00082, 2017.
Luke Metz, Ben Poole, David Pfau, and Jascha Sohl-Dickstein. Unrolled generative adversarial networks. CoRR, abs/1611.02163, 2016.
Augustus Odena, Christopher Olah, and Jonathon Shlens. Conditional image synthesis with auxiliary classifier GANs. In ICML, 2017.
Julien Rabin, Gabriel Peyr, Julie Delon, and Marc Bernot. Wasserstein barycenter and its application to texture mixing. In Scale Space and Variational Methods in Computer Vision (SSVM), pp. 435–446, 2011.
Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. CoRR, abs/1511.06434, 2015.
Tim Salimans and Diederik P. Kingma. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. CoRR, abs/1602.07868, 2016.
Tim Salimans, Ian J. Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. Improved techniques for training GANs. In NIPS, 2016.
Kenneth O. Stanley and Risto Miikkulainen. Evolving neural networks through augmenting topologies. Evolutionary Computation, 10(2):99–127, 2002.
Tijmen Tieleman and Geoffrey E. Hinton. Lecture 6.5 - RMSProp. Technical report, COURSERA: Neural Networks for Machine Learning, 2012.
Dmitry Ulyanov, Andrea Vedaldi, and Victor S. Lempitsky. Adversarial generator-encoder networks. CoRR, abs/1704.02304, 2017.
A¨aron van den Oord, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew W. Senior, and Koray Kavukcuoglu. WaveNet: A generative model for raw audio. CoRR, abs/1609.03499, 2016a.
A¨aron van den Oord, Nal Kalchbrenner, and Koray Kavukcuoglu. Pixel recurrent neural networks. In ICML, pp. 1747–1756, 2016b.
A¨aron van den Oord, Nal Kalchbrenner, Oriol Vinyals, Lasse Espeholt, Alex Graves, and Koray Kavukcuoglu. Conditional image generation with PixelCNN decoders. CoRR, abs/1606.05328, 2016c.
Twan van Laarhoven. L2 regularization versus batch and weight normalization. CoRR, abs/1706.05350, 2017.
Ting-Chun Wang, Ming-Yu Liu, Jun-Yan Zhu, Andrew Tao, Jan Kautz, and Bryan Catanzaro. High-resolution image synthesis and semantic manipulation with conditional GANs. CoRR, abs/1711.11585, 2017.
Zhou Wang, Eero P. Simoncelli, and Alan C. Bovik. Multi-scale structural similarity for image quality assessment. In Proc. IEEE Asilomar Conf. on Signals, Systems, and Computers, pp. 1398–1402, 2003.
David Warde-Farley and Yoshua Bengio. Improving generative adversarial networks with denoising feature matching. In ICLR, 2017.
Jianwei Yang, Anitha Kannan, Dhruv Batra, and Devi Parikh. LR-GAN: Layered recursive generative adversarial networks for image generation. In ICLR, 2017.
Fisher Yu, Yinda Zhang, Shuran Song, Ari Seff, and Jianxiong Xiao. LSUN: Construction of a large-scale image dataset using deep learning with humans in the loop. CoRR, abs/1506.03365, 2015.
Han Zhang, Tao Xu, Hongsheng Li, Shaoting Zhang, Xiaolei Huang, Xiaogang Wang, and Dimitris N. Metaxas. StackGAN: Text to photo-realistic image synthesis with stacked generative adversarial networks. In ICCV, 2017.
Junbo Jake Zhao, Micha¨el Mathieu, and Yann LeCun. Energy-based generative adversarial network. In ICLR, 2017.
Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A. Efros. Unpaired image-to-image translation using cycle-consistent adversarial networks. CoRR, abs/1703.10593, 2017.

A 網絡結構和訓練配置

A.1 用于 CELEBA-HQ 的 1024 × 1024 網絡

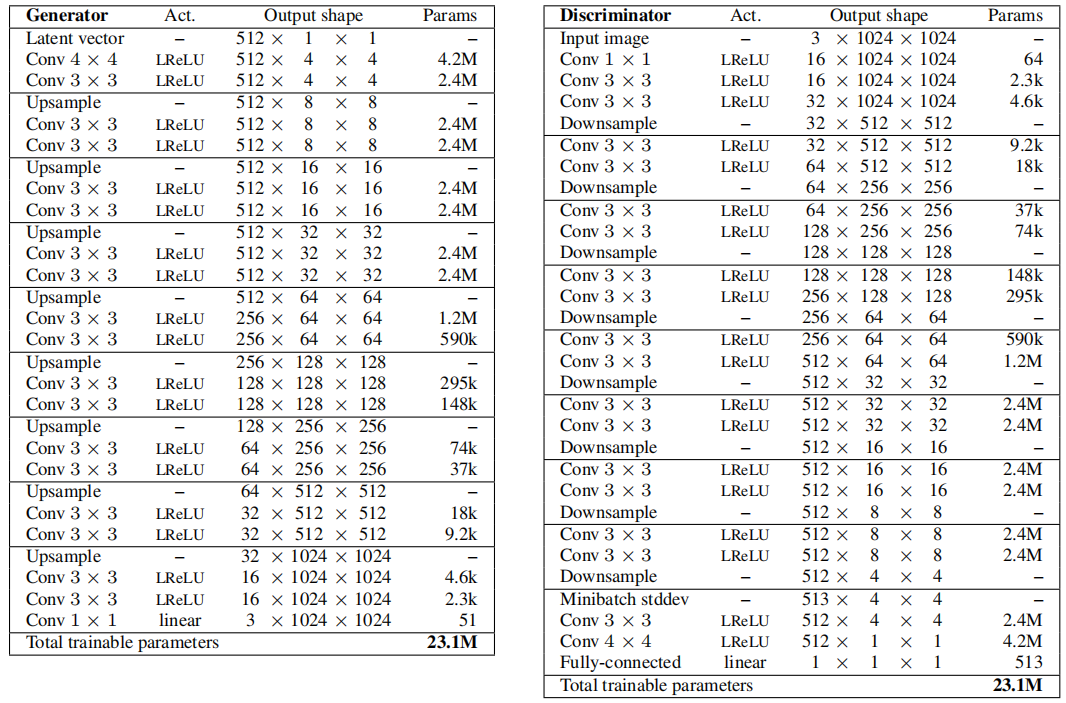
表2展示了我們在 CELEBA-HQ 數據集上使用的完整分辨率生成器和判別器的網絡架構。這兩個網絡主要由逐步引入的3層復制塊組成，訓練過程中逐步引入這些塊。生成器的最后一個 $\times 1$ 卷積層對應于圖2中的 toRGB 塊，判別器的第一個 $\times 1$ 卷積層類似地對應于 fromRGB。我們從 $\times 4$ 分辨率開始訓練網絡，總共向判別器展示了 800k 個真實圖像。然后，我們在接下來的 800k 個圖像中在第一個 3層塊中淡入，再穩定網絡 800k 個圖像，在接下來的 800k 個圖像中淡入下一個 3層塊，以此類推。

表2：我們在 CELEBA-HQ 中使用的生成器和判別器，用于生成 1024×1024 圖像。

潛在向量對應于512維超球面上的隨機點，我們將訓練和生成的圖像歸一化到 $[? 1, 1]$ 范圍內。在兩個網絡的所有層中，除了最后一層使用線性激活函數外，都使用了泄漏整流線性單元（Leaky ReLU），泄漏率為0.2。在任何一個網絡中，我們都沒有使用批歸一化、層歸一化或權重歸一化。但是，在生成器的每個 $\times 3$ 卷積層之后，我們對特征向量進行逐像素歸一化，就像第4.2節中所述。

所有偏置參數都初始化為零，并且所有權重按照單位方差的正態分布進行初始化。然而，我們在運行時使用層特定的常數來縮放權重，正如第4.1節所述。我們將在第3節中描述的過程中，在判別器末尾的 $\times 4$ 分辨率處，注入了跨小批量標準差作為額外的特征圖。表 2 中的上采樣和下采樣操作分別對應于 $\times 2$ 元素復制和平均池化，分別。

訓練過程中使用 Adam 優化器（Kingma & Ba, 2015），其中 $\alpha = 0.001$ ， $\beta_1 = 0$ ， $\beta_2 = 0.99$ ， $\epsilon = 10^{-8}$ 。我們沒有使用任何學習率衰減或降低策略。為了在訓練過程中可視化生成器的輸出，在生成器的權重上使用了指數移動平均，衰減率為0.999。對于分辨率從 $4^2$ 到 $128^2$ 的不同情況，我們使用小批量大小 16，然后逐漸減小大小，分別變為 $256^2 \rightarrow 14$ ， $512^2 \rightarrow 6$ ， $1024^2 \rightarrow 3$ ，以避免超出內存預算。

我們使用了 WGAN-GP 損失，但與 Gulrajani 等人（2017年）不同的是，我們在每個小批量上交替優化生成器和判別器，即設置 $n_{\text{critic}} = 1$ 。此外，我們在判別器損失中引入了第四個項，其權重非常小，以防止判別器輸出偏離零太遠。準確地說，我們設置 $\epsilon_{\text{drift}}E_{x \in P_r} [D(x)^2]$ ，其中 $\epsilon_{\text{drift}} = 0.001$ 。

A.2 其他網絡

對于低于 $1024 \times 1024$ 的空間分辨率，我們在兩個網絡中適當地略去了復制的 3 層塊的數量。

此外，在第 6.1 節中，我們使用了稍低容量的版本，在 $16 \times 16$ 分辨率的 Conv $\times 3$ 層中減少了特征映射的數量，隨后在后續分辨率中減少了4倍。這使得最后一個 Conv $\times 3$ 層有32個特征映射。在表1和圖4中，我們對每個分辨率進行了總共 600k 張圖像的訓練，而不是 800k 張，并在 600k 張圖像的持續時間內淡入新層。

對于表1中的 “Gulrajani 等人（2017年）” 情況，我們盡量遵循他們的訓練配置。具體來說，包括 $\alpha = 0.0001$ ， $\beta_2 = 0.9$ ， $n_{\text{critic}} = 5$ ， $\epsilon_{\text{drift}} = 0$ ，和小批量大小為 64。禁用了漸進式分辨率、小批量標準差以及運行時的權重縮放，所有權重都使用了 He 初始化器（He et al., 2015）。此外，在生成器中，我們用 ReLU 替換了 LReLU，將最后一層的線性激活改為 tanh，將逐像素歸一化改為批歸一化。在判別器中，對所有 Conv $\times 3$ 和 Conv $\times 4$ 層添加了層歸一化。潛在向量由從正態分布獨立采樣的 128 個分量組成。

B 1024 × 1024 的最小二乘生成對抗網絡 (Least-Squares GAN, LSGAN)

我們發現 LSGAN 通常比 WGAN-GP 更不穩定，而且在長時間運行結束時也容易失去一些變化。因此，我們更傾向于使用 WGAN-GP，但也通過在 LSGAN 的基礎上構建來生成高分辨率圖像。例如，圖1中的 10242 圖像是基于 LSGAN 的。

除了在第 2 至 4 節中描述的技術之外，我們在 LSGAN 中還需要一個額外的“hack”，以防止在數據集對于判別器來說過于簡單的情況下訓練失控，導致判別器梯度失去意義。我們會根據判別器的輸出，自適應地增加判別器中的乘性高斯噪聲的幅度。這個噪聲會應用于每個 Conv $\times 3$ 和 Conv $\times 4$ 層的輸入。歷史上一直有在判別器中添加噪聲的做法，但通常會對圖像質量產生負面影響（Arjovsky et al., 2017）。理想情況下是不需要這樣做的，而根據我們的測試結果，對于 WGAN-GP（Gulrajani et al., 2017）來說，這是成立的。噪聲的幅度由公式 $0.2 \cdot \max(0, \hat{d}_t - 0.5)^2$ 決定，其中 $\hat{d}_t = 0.1d + 0.9\hat{d}_{t-1}$ 是判別器輸出 $d$ 的指數移動平均。這個“hack”的動機是，當 $d$ 接近（或超過）1.0 時，LSGAN 會變得非常不穩定。

C CELEBA-HQ 數據集

在本節中，我們描述了創建高質量版本的 CELEBA 數據集的過程，該數據集包含 30000 張 $1024 \times 1024$ 分辨率的圖像。作為起點，我們采用了原始 CELEBA 數據集中包含的各種野外圖像集合。這些圖像在分辨率和視覺質量方面變化極大，從 $43 \times 55$ 到 $6732 \times 8984$ 不等。其中一些圖像顯示了數人的人群，而其他圖像則集中在單個人的面部上 - 往往只是面部的一部分。因此，我們發現有必要應用多種圖像處理步驟，以確保一致的質量并將圖像居中在面部區域。

我們的處理流程如圖8所示。為了提高整體圖像質量，我們使用兩個預訓練的神經網絡對每個 JPEG 圖像進行預處理：一個卷積自編碼器，用于消除自然圖像中的 JPEG 噪點，結構類似于 Mao 等人（2016a）的提出的方法；以及一個經過對抗訓練的 4x 超分辨率網絡（Korobchenko & Foco, 2017），類似于 Ledig 等人（2016）。為了處理面部區域超出圖像的情況，我們使用填充和濾波來擴展圖像的尺寸，如圖8（c-d）所示。

圖8：創建 CELEBA-HQ 數據集。我們從 CelebA 野外數據集中獲取 JPEG 圖像 (a)。我們通過去除 JPEG 圖像偽影（b，頂部）和 4 倍超分辨率（b，底部）來提高視覺質量（b，中部）。然后，我們通過鏡像填充（c）和高斯濾波（d）來擴展圖像，以產生視覺上令人愉悅的景深效果。最后，我們使用面部標志位置選擇適當的裁剪區域 (e)，并執行高質量的重采樣以獲得最終的 1024 × 1024 分辨率圖像 (f)。

然后，根據原始 CELEBA 數據集中包含的面部標志注釋，我們選擇一個面部裁剪矩形，具體如下：

$\begin{align} x' = & e_1 - e_0 \\ y' = & \frac{1}{2} (e_0 + e_1) - \frac{1}{2} (m_0 + m_1) \\ c = & \frac{1}{2} (e_0 + e_1) - 0.1 \cdot y' \\ s = & \max (4.0 \cdot |x'|, 3.6 \cdot |y'|) \\ x = & \text{Normalize} (x' - \text{Rotate90}(y')) \\ y = & \text{Rotate90}(x') \end{align}$

其中， $e_0$ 、 $e_1$ 、 $m_0$ 和 $m_1$ 分別表示兩個眼睛標志和兩個嘴巴標志的 2D 像素位置， $c$ 和 $s$ 表示所需裁剪矩形的中心和尺寸， $x$ 和 $y$ 表示其方向。我們通過經驗構建了上述公式，以確保在不同角度觀察面部時，裁剪矩形保持一致。計算出裁剪矩形后，我們使用雙線性濾波將矩形變換為 $4096 \times 4096$ 像素，然后使用盒式濾波將其縮放為 $1024 \times 1024$ 分辨率。

我們對數據集中的所有 202599 張圖像執行上述處理，進一步分析生成的 $1024 \times 1024$ 圖像以估計最終的圖像質量，按照質量對圖像進行排序，并丟棄除了最佳的 30000 張圖像之外的所有圖像。我們使用基于頻率的質量度量標準，這有利于包含廣泛頻率范圍并且大致呈徑向對稱的功率譜的圖像。這懲罰了模糊圖像以及由于可見的半色調模式等原因具有顯著方向特征的圖像。我們選擇了 30000 張圖像作為實際的最佳結果的平衡點，因為這似乎產生了最好的結果。

D CIFAR10 結果

圖9展示了在無監督設置下生成的非精選圖像，表3則比較了基于 Inception 分數的先前方法。我們以兩種不同的方式報告分數：1) 訓練運行過程中觀察到的最高分數（這里的 ± 表示 Inception 分數計算器返回的標準偏差）；2) 從訓練中觀察到的最高分數中計算的均值和標準偏差，從十個隨機初始化開始。可以說，后一種方法更有意義，因為個別運行可能會出現幸運情況（就像我們的情況）。在這個數據集中，我們沒有使用任何形式的數據增強。

表3：CIFAR10 Inception 分數，分數越高越好。

圖9：使用無監督訓練的網絡（無標簽條件），生成的 CIFAR10 圖像，獲得了創紀錄的 8.80 Inception 分數。

E MNIST-1K 離散模式測試與喪失能力的判別器

Metz 等人（2016）描述了一個設置，其中生成器同時合成 MNIST 數字到 3 個顏色通道，使用預訓練分類器對數字進行分類（在我們的情況下為 0.4% 的錯誤率），然后連接在一起形成 [0, 999] 范圍內的數字。他們生成了總共 25600 張圖像，并計算覆蓋的離散模式數量。他們還計算 KL 散度，即 KL（直方圖 || 均勻分布）。現代 GAN 實現可以在非常低的散度下輕松覆蓋所有模式（在我們的情況下為 0.05），因此 Metz 等人指定了一個相當低容量的生成器和兩個喪失能力的判別器（“K/2” 約有 2000 個參數，“K/4” 只有約 500 個），以揭示訓練方法之間的差異。這兩個網絡都使用了批歸一化。

如表4所示，使用 Metz 等人指定的網絡結構以 WGAN-GP 損失覆蓋的模式要比原始 GAN 損失多得多，甚至比使用較小的（K/4）判別器的未展開的原始 GAN 更多。KL 散度，這可能是一個比原始計數更準確的指標，效果更好。

表4：使用 Metz 等人（2016）定義的兩個微小判別器（K/4、K/2）進行 MNIST 離散模式測試的結果。覆蓋的模式數量 (#) 和與均勻分布的 KL 散度給出了在 8 個隨機初始化上的平均值 ± 標準偏差。對于模式數量，越高越好，對于 KL 散度，越低越好。

將批歸一化替換為我們的標準化（均衡學習率、逐像素標準化）顯著改善了結果，同時還從判別器中刪除了一些可訓練參數。添加小批量標準差層進一步改善了分數，同時將判別器的容量恢復到原始容量的 0.5%。對于這些小圖像，漸進式方法并沒有太大幫助，但也沒有損害。

F 額外的 CELEBA-HQ 結果

圖10展示了我們生成圖像的最近鄰。圖11給出了來自 CELEBA-HQ 的額外生成示例。我們對使用 CELEBA 和 CELEBA-HQ 進行的所有測試都啟用了鏡像增強。除了切片 Wasserstein 距離 (SWD) 外，我們還引用了最近引入的 Fréchet Inception 距離 (FID) (Heusel 等人，2017)，從 50K 張圖像計算而來。

圖10：頂部：我們的 CELEBA-HQ 結果。接下來的五行：從訓練數據中找到的最近鄰，基于特征空間距離。我們使用了來自五個 VGG 層的激活值，如 Chen & Koltun（2017）所建議的。只有在右下圖像中突出顯示的裁剪區域用于比較，以排除圖像背景，并將搜索重點放在匹配的面部特征上。

圖11：使用 CELEBA-HQ 數據集生成的其他 1024×1024 圖像。切片 Wasserstein 距離（SWD）×103 在 1024、…、16 層次上分別為 7.48、7.24、6.08、3.51、3.55、3.02、7.22，其平均值為 5.44。從 5 萬張圖像計算的 Fréchet Inception 距離（FID）為 7.30。請參見視頻以獲取潛在空間插值。

G LSUN 結果

圖12-17展示了為所有 30 個 LSUN 類別生成的代表性圖像。為每個類別單獨訓練了一個網絡，使用相同的參數。所有類別都使用了 100K 張圖像進行訓練，除了 BEDROOM 和 DOG，它們使用了所有可用數據。由于對于大多數類別來說，100K 張圖像是非常有限的訓練數據，因此我們在這些測試中啟用了鏡像增強（但不適用于 BEDROOM 或 DOG）。

圖12：從 LSUN 類別生成的 $256 \times 256$ 示例圖像。切片 Wasserstein 距離（SWD） $×103 \times 10^3$ 分別給出了 256、128、64、32 和 16 層次，其中平均值用粗體表示。我們還引用了從 5 萬張圖像計算的 Fréchet Inception 距離（FID）。

圖13：從 LSUN 類別生成的 $256 \times 256$ 示例圖像。切片 Wasserstein 距離（SWD） $×103 \times 10^3$ 分別給出了 256、128、64、32 和 16 層次，其中平均值用粗體表示。我們還引用了從 5 萬張圖像計算的 Fréchet Inception 距離（FID）。

圖14：從 LSUN 類別生成的 $256 \times 256$ 示例圖像。切片 Wasserstein 距離（SWD） $×103 \times 10^3$ 分別給出了 256、128、64、32 和 16 層次，其中平均值用粗體表示。我們還引用了從 5 萬張圖像計算的 Fréchet Inception 距離（FID）。

圖15：從 LSUN 類別生成的 $256 \times 256$ 示例圖像。切片 Wasserstein 距離（SWD） $×103 \times 10^3$ 分別給出了 256、128、64、32 和 16 層次，其中平均值用粗體表示。我們還引用了從 5 萬張圖像計算的 Fréchet Inception 距離（FID）。

圖16：從 LSUN 類別生成的 $256 \times 256$ 示例圖像。切片 Wasserstein 距離（SWD） $×103 \times 10^3$ 分別給出了 256、128、64、32 和 16 層次，其中平均值用粗體表示。我們還引用了從 5 萬張圖像計算的 Fréchet Inception 距離（FID）。

圖17：從 LSUN 類別生成的 $256 \times 256$ 示例圖像。切片 Wasserstein 距離（SWD） $×103 \times 10^3$ 分別給出了 256、128、64、32 和 16 層次，其中平均值用粗體表示。我們還引用了從 5 萬張圖像計算的 Fréchet Inception 距離（FID）。